因果推理导论第4课 后门调整方法与结构因果模型
- 一、前言
- 二、do算子与干预分布
- 三、模块化假设
- [四、后门调整(Backdoor Adjustment)](#四、后门调整(Backdoor Adjustment))
- 五、结构因果模型(SCMs)
- 六、案例
- 七、总结
一、前言
前面介绍了因果图的基本概念,这一章在因果图上,从理论工具(do 算子、模块化假设)出发,推导出关键的后门调整方法,并结合结构因果模型(SCM)进行理论落地,最终通过实例验证从关联相关到因果效应识别方法的有效性。
二、do算子与干预分布
回忆一下前面第一课就在说的治疗的例子,治疗为1,不治疗为0,想知道治疗到底有没有效果,理想方法是做实验,对目标一遍治疗,与不做治疗进行两个效果的对比;这种方式就是干预intervening(针对全部群体进行) ,当然实际中,一个人做了治疗就不能再得到不做治疗的效果;所以我们只能选择一部分群体做治疗,一部分群体不做治疗,来观察其效果,这种就是条件观测conditioning .前者表示对变量进行干预操作,区别于普通的条件概率
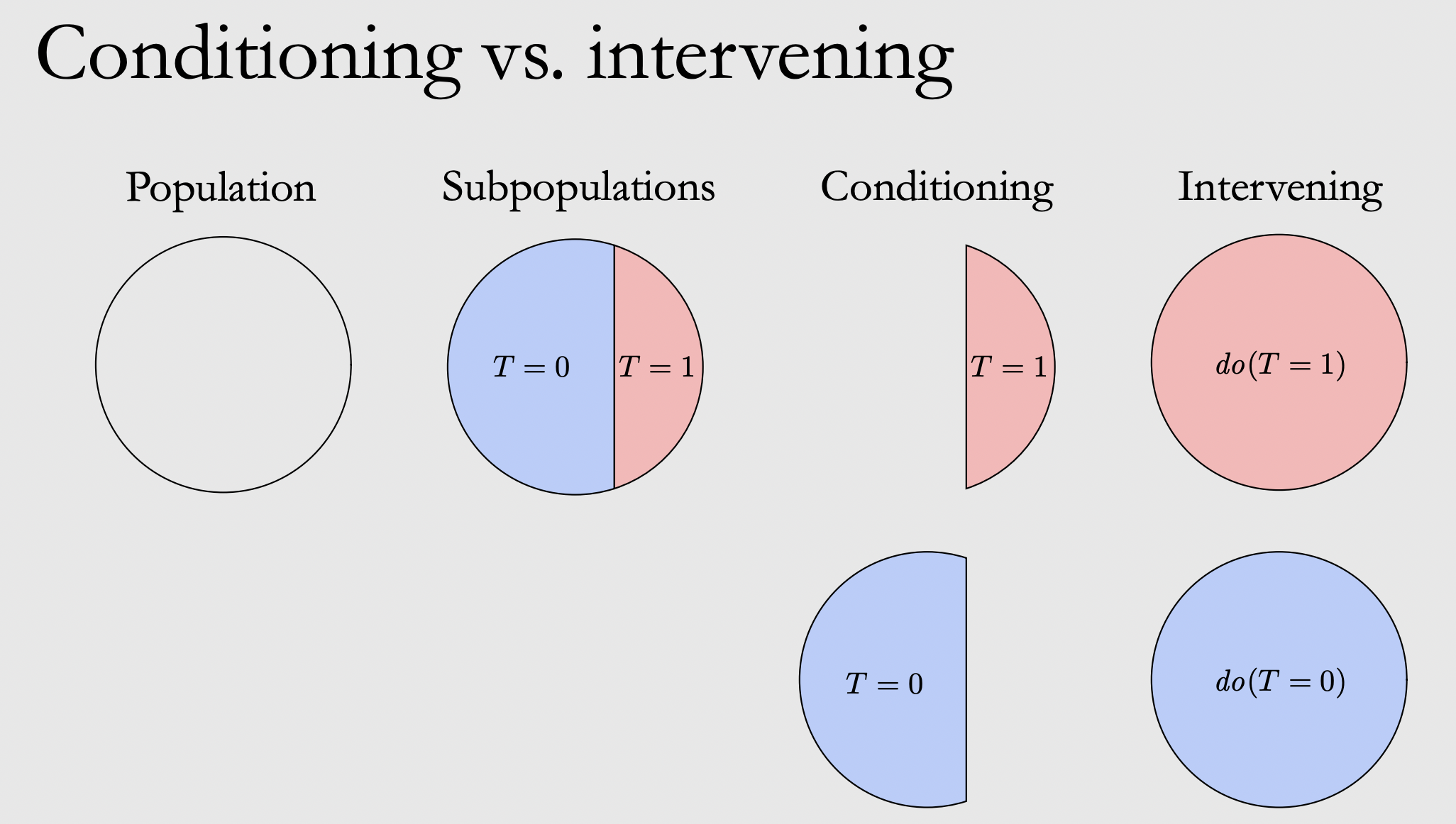
这个干预是理想上的,跟前面说的潜在效应意思是一致的,我们用数学符号do()来表示干预动作,这样治疗的效应公式就改写为下面形式,其中观测的分布表示与干预的分布表示差异如下图所示,其含义为P(Y|do(T)) 代表干预 T 后的结果分布,P(Y|T) 仅代表观测到 T时的关联分布.

为什么要定义一个do-算子,引入干预分布呢,其原因在于在第3课提到的因果效应计算流程,先得到因果估计,然后转为概率估计进行计算,实际怎么转的过程,上一节并没有详细说明,上一节中默认我们已经有了因果图,根据因果图与贝叶斯公式,马尔可夫假设就可以得到因果估计式子,然后就转为概率估计了;实际上我们需要通过干预得到的概率分布,用于量化因果效应,从而转为概率估计 ,然后再根据观测值结合机器学习等算法进行估计得到最终效应.
因此干预是从 "关联" 走向 "因果" 的桥梁 .

三、模块化假设
接下来,来给出通过干预,进行因果识别前的一个基础核心假设.如果我们干预了一些节点,把它们设置为常数,那么对于节点i来说,如果它不在干涉节点里,那么它的关系没有发生变化,否则,其与干预信息一致的话是1,不一致就是0.

案例如下,对T进行干预,T=t,那么不管它的父节点如何变化都不影响T,因为此时T已经变成一个常数,因此T节点与其父节点的相关性就被切断了,这样它们之间的边可被去掉.再如图©,干预T2,其变化类似T节点.
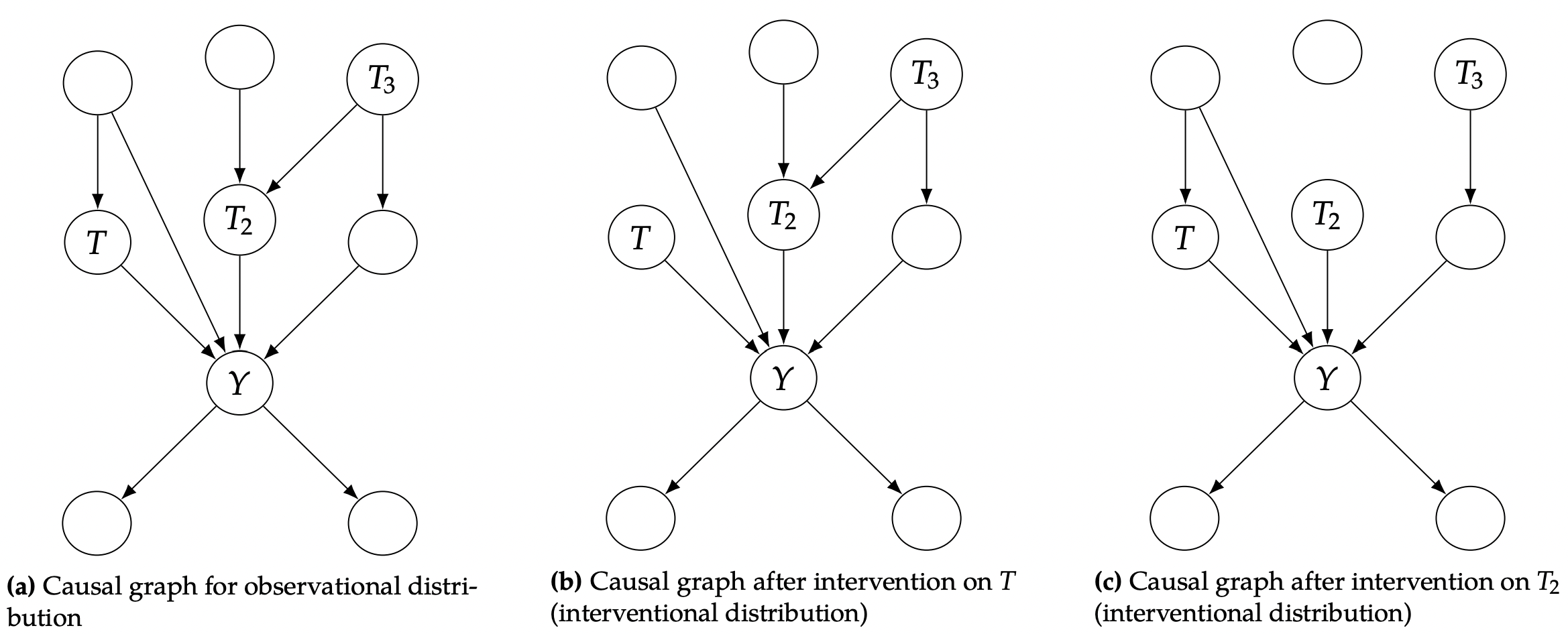
那么因果图在干预下发生了大的变化,其对应的贝叶斯公式也会发生相应的变化,整合起来得到下面的 Truncated Factorization定理.如果P(概率分布)与G(因果图)都符合马尔可夫假设和模块化假设,那么其概率分布在有干预的下的变化如4.1所示.pai是xi的父节点

有了干预改变分布后,那是不是就改变了其相关性呢,我们来看个例子,我们对T做干预,那么贝叶斯网络P(y,x,t)中的p(t|x)就没有了,因为T做了do,那么x与t的关系被切断;想求y,那么再对X取边际期望,就得到了.
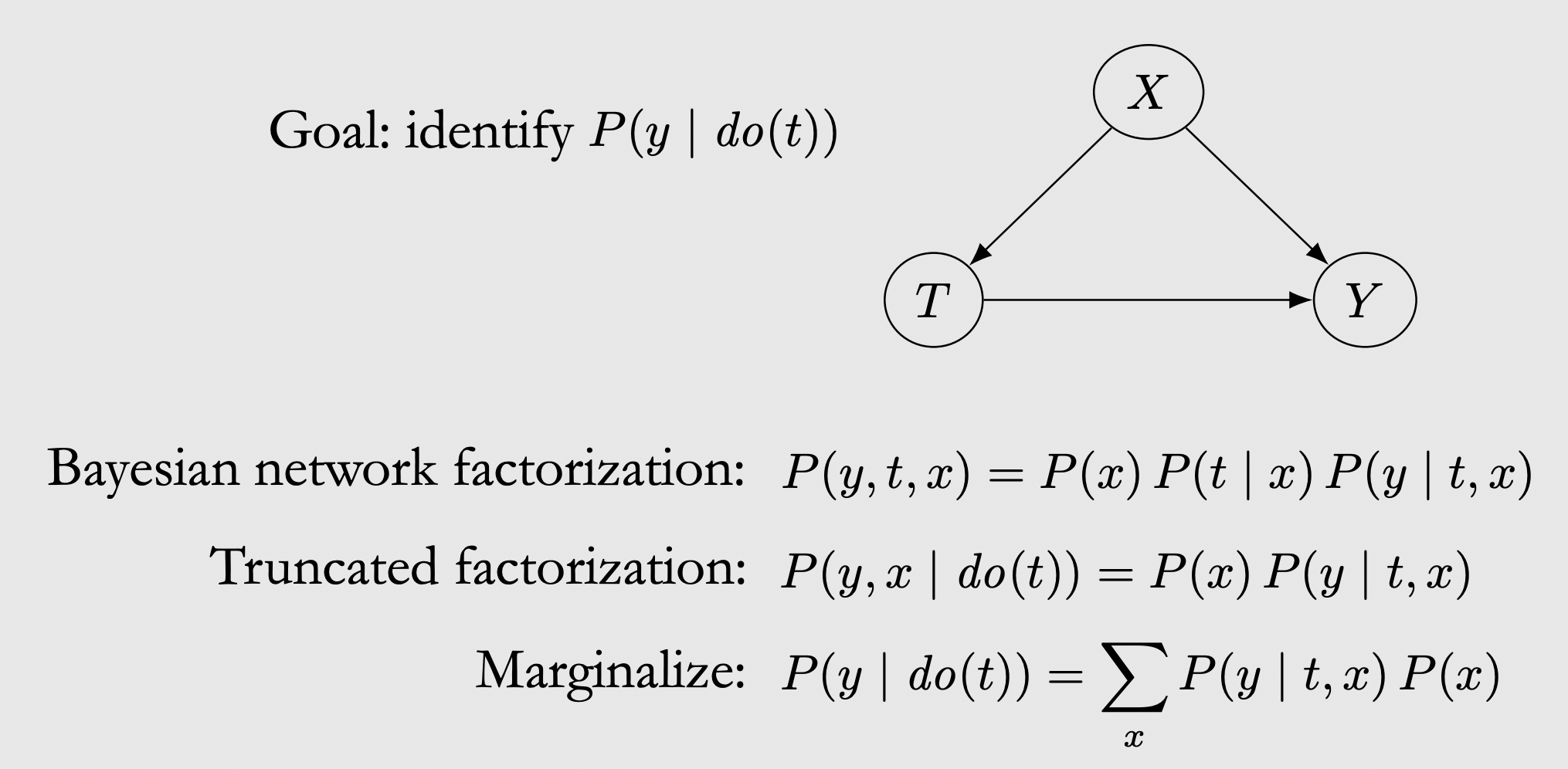
如果我们在不做do的情况下,求取y的话,其计算是什么样的呢,其对比如下所示,其P(x)变为P(x|t),这里就可以看到do操作确实可以有效改变其相关性 ,进一步我们就可以使用这个方法,去除因果图中的相关性,这样剩下的因果性(父节点是所有子节点的因)就可以进行求取;比如下面这个图中,要求T对Y的因果效应,在去除x与t的相关性后,我们就可以得到P(y|do(t)),根据该式子与观测值进行估计计算,得到最终因果效应值.

接下来我们更加正式的给出其因果量化的方法.
四、后门调整(Backdoor Adjustment)
后门准则:W节点集合可以堵住所有从T到y的后路(如前面的图,除了T直接到y,还有x到y,t有一条入边来自x),W不包含T的任意子节点.那么W就符合后面准则.

因为后路涉及到的节点可能不止一个,所以使用W集合来表示,同时应用模块化假设与正值假设,其因果效应就变为,这个公式就是后门调整公式
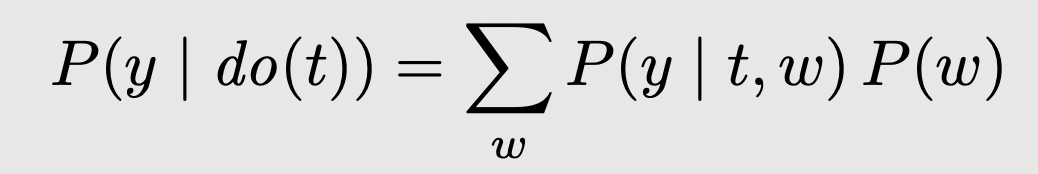
五、结构因果模型(SCMs)
1、SCMs定义
因果贝叶斯网络为我们提供了编码统计和计算因果假设的强有力方法,但我们尚未确切解释什么是干预,也未确切解释什么是因果机制。从因果贝叶斯网络到完整的结构因果模型,将让干预,因果机制更清晰,同时具备计算反事实的能力。
常用的数学方程如A=B ,B=A 这种等式通常是对称的,当然因果是由什么因得到什么果,是不对称的形式,这样其结构方程表示为B由A通过结构f映射得到,当然实际场景中除了已知的A,还有一些未知的因素影响这个映射过程 ,所以将结构方程改写为4.23

其中的U代表的就是未知的随机变量

函数 f 的函数形式不需要被指定;当它未被指定时,我们处于非参数(nonparametric)范畴,因为我们没有对参数形式做任何假设。虽然该映射是确定性(deterministic)的,但它还有一个随机变量 U(即 "噪声" 或 "背景条件" 变量),可以表示任何随机(stochastic)映射。因此,结构方程推广了我们一直使用的概率分布 P(Xi∣PAi)。之前说到的仍然成立 ------ 例如截断因式分解(truncated factorization)和后门调整(backdoor adjustment)------ 在引入结构方程后仍然成立。
当然结构有可能会更复杂,如下图所示,其中B由A与随机变量UB得到,C由A,B,UC得到,D由A,C,UD得到,这样其结构方程如M所示,其节点含义如SCM定义所示.

2、模块化假设
结构方程与模型定义已经有了,接下来看看其干预在结构方程上的表示,可以看到在结构方程上,模块化假设仍然成立.
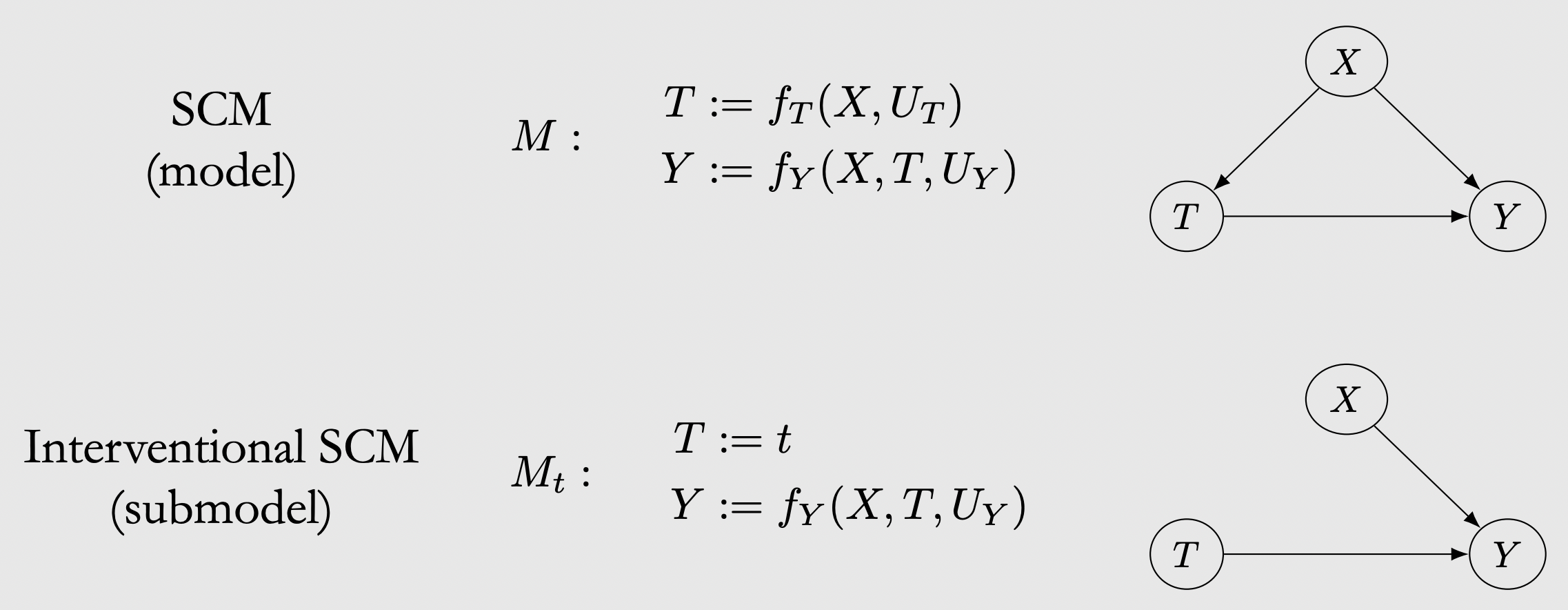
将模块化假设,使用SCM模型表述方式进行表达,其表示如下,其干预前后表示为M,Mt

3、后门调整条件思考🤔
后门调整准则里面有两点,其中一点是do的W集合不包含T的任意子节点,这里通过子节点不同结构进行辅助说明
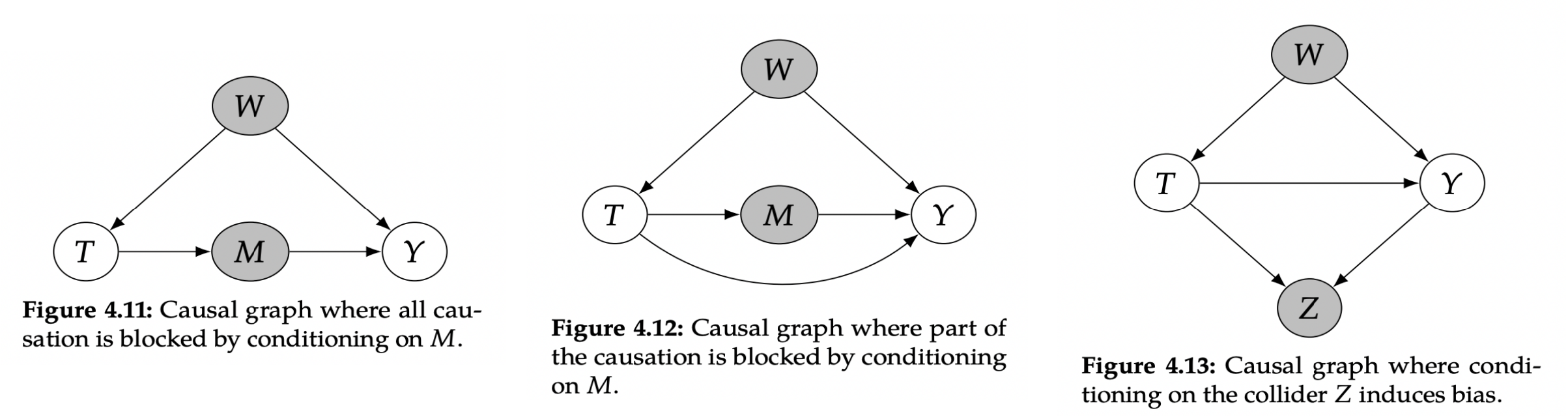
- 图4.11如果子节点在T到Y节点上的,直观上就明白其直接阻断了T到Y的因果关系,使得原本的因果效应变为0.
- 图4.12 T到Y有直接边,do M,会有部分因果关系被阻断,同样影响原本T对Y的因果效应.
- 图 4.13 Z的结构是对撞结构,不干预时,T与Y无相关性,干预,两者增加了相关性,使得T对Y的原始因果效应中增加了混杂的相关性.
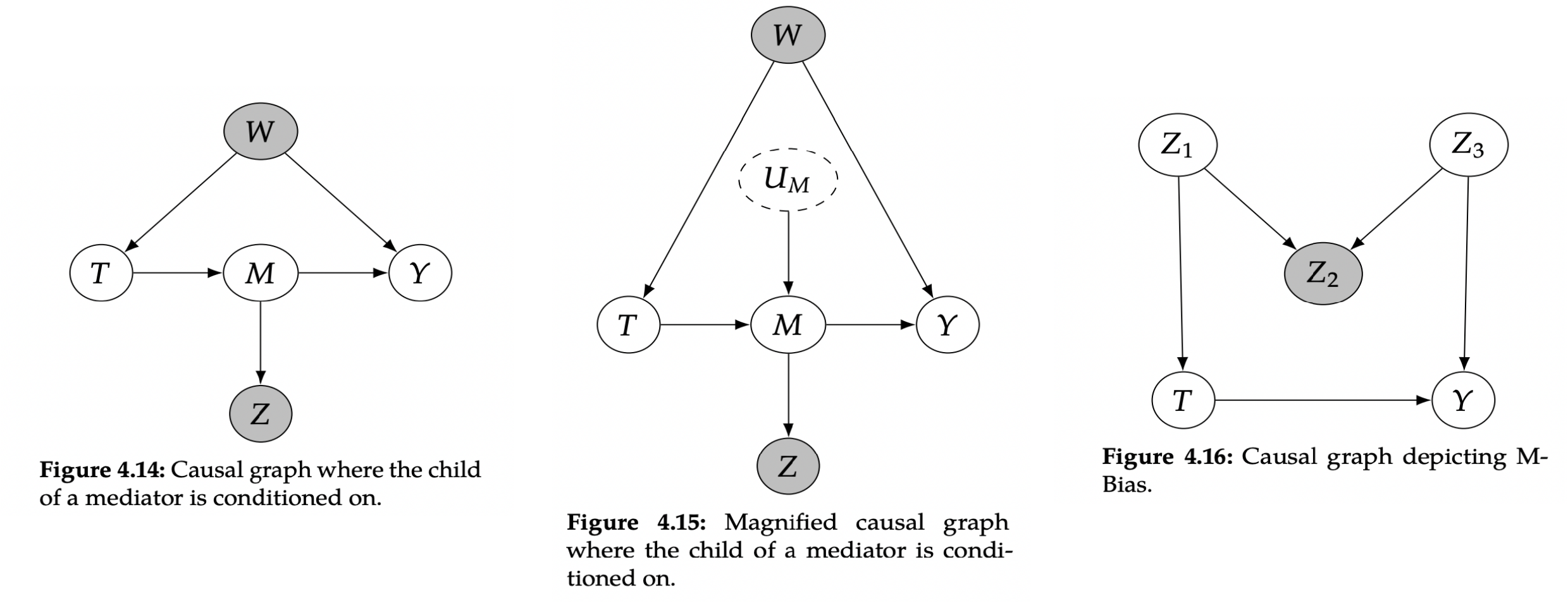
- 图4.14 Z是M的子节点,单看看不出来,再结合图4.15,将M的noisUM 画出来,干预Z,使得T与UM有相关性,其通过了边T➡️M,同时边T➡️M有到Y的因果性,直观上感觉这条边在做干预后混杂了新的信息,因此也会影响原本T对Y的因果效应.(具体论证见后续章节)
- 图4.16 里展示了即使我们只对处理前协变量(pretreatment covariates)进行条件控制,我们仍然可能诱导出对撞机偏差。对 Z2 进行干预,会打开一条后门路径(backdoor path),非因果关联性可以沿着该路径流动。这被称为M 型偏差(M-bias),从而影响原本T对Y的因果效应.
六、案例
接下来用这章学习的方法进行一个完整因果估计.
- 背景:研究纳的摄入对高血压的因果效应
- 设置:纳摄入超过3.5mg为1,否则为0
- 影响因子:纳摄入,年龄,尿蛋白,其因果结构模型如下图所示
- 解决方案:因果效应估计目标如图右侧,其正常统计的观测估计是将相关因素都纳入;在因果结构模型下,可以看到Z干预会影响因果效应估计,因此修正为最后的式子,进行统计上的估计;Ew通过求均值得到,E(Y|t,W)由机器学习模型得到
- 验证先验信息:哪摄入为1的因果效应是1.05

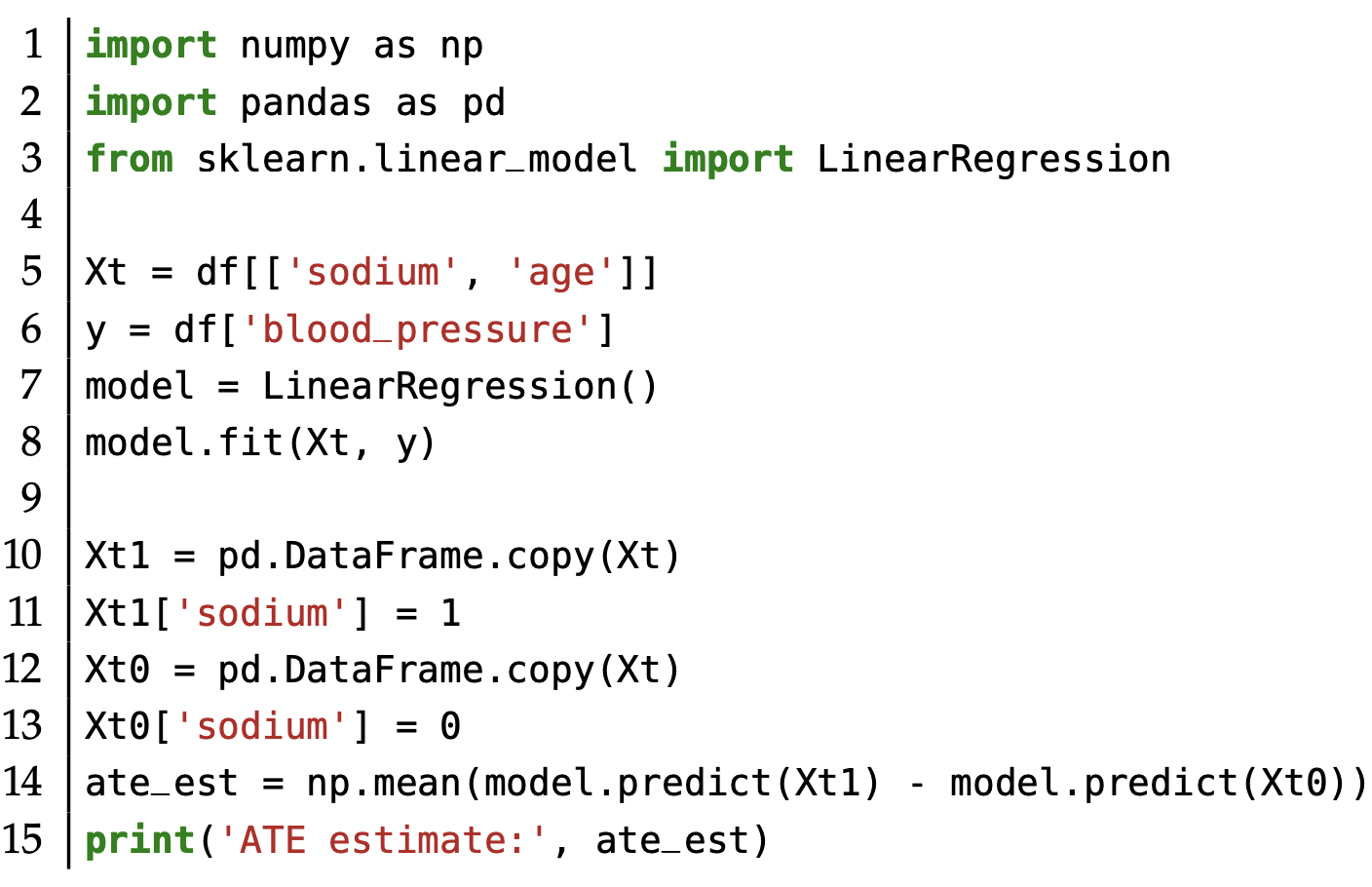
其具体代码操作如下所示,其变量为t,W ,目标为Y,使用线性模型进行拟合,然后计算在所有w下t=1,与0的效应均值,其结果为1.0502,与验证值误差0.02%很小,说明结果正确; 若直接对t,Y 进行回归,其误差为400%;若不做干预,其结果误差为19%.该 实验过程说明了干预与因果结构模型的意义
七、总结
本章的目标是解决一个核心问题:如何从观测数据中计算出干预(Treatment)对结果(Outcome)的因果效应?
- 引入 do-算子 来定义干预,区分 "看到"(观测)和 "做"(干预)这两种行为。
- 提出模块性假设(Modularity),作为干预下因果机制不变的理论基础。
- 推导出截断因式分解,展示干预后联合分布的计算方式。
- 给出最核心的实用工具:后门调整公式,并说明其与潜在结果框架的联系。
- 引入更底层的结构因果模型(SCMs),统一因果机制、干预和反事实的表达。
- 强调常见陷阱:对撞机偏差,以及为什么不能控制处理变量的后代。
最后回顾一下关键假设,模块假设从因果模型(贝叶斯网络)到因果结构模型;马尔可夫假设从局部假设到贝叶斯网络因子到全局假设.
