数据结构基础：堆高效数据结构全面解析

1、什么是堆？

想象你是医院急诊科的分诊护士。每天有大量病人就诊，紧急程度各不相同：

🚨 危重病人（优先级10）--- 心脏病突发，必须立即抢救
⚠️ 紧急病人（优先级7）--- 骨折，需要尽快处理
🤕 普通病人（优先级5）--- 发烧、肚子疼
💊 轻症病人（优先级1）--- 普通感冒

你的职责：快速找到最紧急的病人、新病人快速插入、处理完后立即找下一个最紧急的。

这就是堆要解决的核心问题！ 层级分明，父节点总是有某种"优势"。

在数据结构中，堆（Heap） 是一个我们看起来像树，但实际上通常用数组存储的数据结构。它必须满足以下两个核心条件：

结构上：它必须是一棵完全二叉树。
性质上：它必须满足堆序性。

前置知识，完全二叉树回顾，一棵完全二叉树是指，除了最后一层外，其他各层节点数都达到最大，并且最后一层的节点都连续集中在左侧。

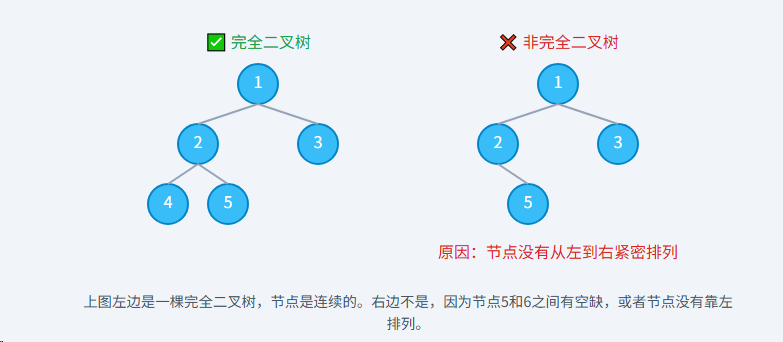
为什么堆要基于完全二叉树？ 这是为了实现高效存储。完全二叉树的结构非常规整，没有"空隙"，这使得我们可以非常方便地用一个连续的数组来表示它，而无需使用指针，从而节省空间并能快速定位父子节点。

2、堆的类型

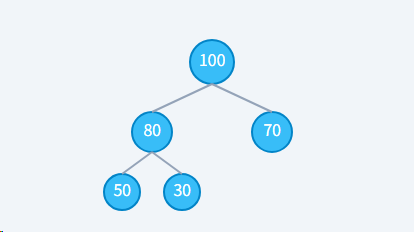
2.1、最大堆

任意父节点的值 ≥ 它的子节点的值。
特点：堆顶元素是整个堆中的最大值。

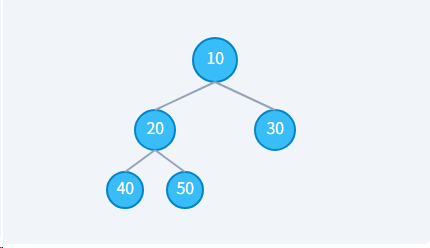
2.2、最小堆

任意父节点的值 ≤ 它的子节点的值。
特点：堆顶元素是整个堆中的最小值。

:::warning
注意： 堆只保证了父子节点之间的关系，但不保证兄弟节点之间的大小关系。例如，在最大堆中，左子节点可能大于、小于或等于右子节点。

:::

3、堆的核心性质

我们已经知道堆有两大性质：结构上是完全二叉树，数值上满足堆序性。但为什么要这样设计？理解这背后的"权衡与选择"是真正掌握堆的关键。

3.1、性质一：完全二叉树

**核**心目的：实现效率与空间的完美平衡。

空间效率： 因为结构紧凑，没有空隙，所以可以用数组来存储。相比于使用指针连接节点的常规树结构，数组表示法完全不需要额外的存储空间来存放指针，极大地节约了内存。
时间效率： 数组存储带来了另一个巨大优势------O(1) 复杂度的寻址 。我们可以通过简单的数学公式（如 2*i+1）快速定位到任意节点的子节点或父节点。这种计算上的直接性远比通过指针逐级遍历要快，尤其是在硬件层面，连续的数组内存布局对 CPU 缓存也更为友好。

"完全二叉树"的结构，是堆能够高效地用数组表示的根本原因。

3.2、性质二：堆序性

核心目的：用"最小的代价"换取"最大的收益"。

这里的"最大收益"指的是能够以 O(1) 的时间复杂度获取集合中的最值（最大或最小）。为了达到这个目的，我们来看两种极端情况：

完全无序 (普通数组)： 找最值需要遍历整个数组，复杂度为 O(N)。代价小，收益也小。
完全有序 (排序数组)： 获取最值是 O(1)，但为了维持这种"完全有序"，每次插入或删除元素都需要移动大量元素，复杂度为 O(N)。收益大，代价也巨大。

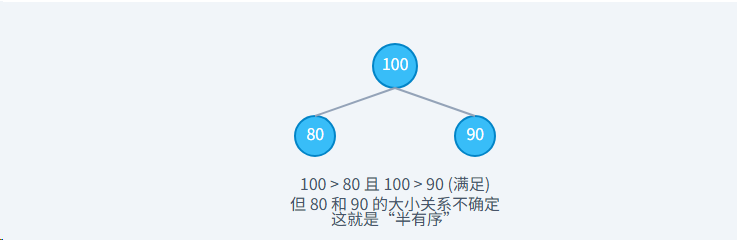
堆则选择了中间路线，即 "部分有序" 或 "半有序"。它只做了一件事：

"我只保证任何一个父节点都比它的所有子孙节点'更优'（更大或更小），至于兄弟之间、堂兄弟之间谁大谁小，我不在乎。"

这种"不在乎"正是堆效率的来源。因为它放弃了对全局排序的执着，所以每次调整（上浮/下沉）只需要沿着一条从根到叶子的路径进行，这条路径的长度是树的高度，即 log N。最终，堆用 O(log N) 的维护代价，换来了 O(1) 的最值查询收益，这笔交易在很多应用场景中都极其划算！

4、堆的存储

虽然我们为了方便理解，总是把堆画成一棵树，但在计算机中，我们几乎总是用数组来存储它。这得益于它"完全二叉树"的优美结构。

我们将树的节点从上到下，从左到右依次存入数组中。

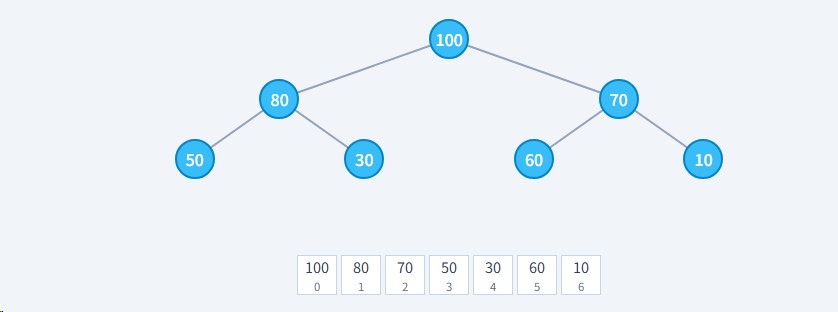
按照层序遍历（从上到下，从左到右）将节点存入数组
数组索引从 0 开始
完全二叉树保证数组没有空洞，空间利用率100%

4.1、索引关系

当堆存储在数组中时，我们可以通过简单的数学运算找到任何节点的父节点和子节点，而无需任何指针。假设一个节点的索引是 i (数组从0开始)：

它的父节点索引是：floor((i - 1) / 2)
它的左子节点索引是：2 * i + 1
它的右子节点索引是：2 * i + 2

例如： 索引为 3 的节点 (值为50)，它的父节点是 floor((3-1)/2) = 1 (值为80)，左子节点是 2*3+1 = 7 (超出范围)，右子节点是 2*3+2=8 (超出范围)。这与树的结构完全吻合！

为什么是这样？ 这正是完全二叉树的性质决定的。每一层节点的数量大约是上一层的两倍。当你把它们平铺到数组里时，这种2倍的关系就体现在了索引的乘法和除法上。

下面我们看一下证明：

4.1.1、证明子节点索引

基础情况 (i=0): 根节点在索引 0。它的左子节点是第2个元素，索引为 1；右子节点是第3个元素，索引为 2。
- 2*0 + 1 = 1 (左子节点)
- 2*0 + 2 = 2 (右子节点)
基础情况成立。
归纳推理: 假设对于节点 i 之前的所有节点 (0, 1, ..., i-1)，这个规律都成立。现在我们来推导节点 i 的子节点位置。
数组中节点的排列顺序是：[节点0, 节点1, ..., 节点i-1, 节点i, ...]。
按照层序遍历的规则，节点 i 的子节点必须排在它前面所有节点 (0 到 i-1) 的所有子节点之后。

节点 0 的子节点是 1, 2。
节点 1 的子节点是 3, 4。
...
节点 i-1 的子节点是 2*(i-1) + 1 和 2*(i-1) + 2。
我们可以看到，节点 i-1 的右子节点占据了索引 2i - 2 + 2 = 2i。所以，节点 0 到 i-1 的子节点总共占据了从索引 1 到索引 2i 的位置。
因此，下一个可用的位置，也就是节点 i 的左子节点 的位置，就是 2i + 1。
它的右子节点 则紧随其后，位置是 (2i + 1) + 1 = 2i + 2。
证明成立。

4.1.2、证明父节点索引

这个证明是子节点索引的逆运算。

假设一个子节点的索引为 c，它的父节点索引为 p。

如果 ** **c** **是左子节点： 根据我们刚才的证明，有 c = 2*p + 1。
解这个方程得到 p = (c - 1) / 2。
如果 ** **c** **是右子节点： 我们有 c = 2*p + 2。
解这个方程得到 p = (c - 2) / 2。

现在的问题是如何用一个公式统一这两种情况。让我们利用整数除法（向下取整）的特性：

对于左子节点 c，c-1 是一个偶数，所以 (c-1)/2 的结果和 floor((c-1)/2) 是一样的。
对于右子节点 c (c > 0)，它是一个偶数，所以 c-1 是一个奇数。 floor((c-1)/2) 的结果和 (c-2)/2 是一样的。（例如, floor((4-1)/2) = floor(1.5) = 1，而 (4-2)/2 = 1）。

因此，无论子节点是左是右，我们都可以用统一的公式 p = floor((c - 1) / 2) 来计算它的父节点。证明成立。

5、堆的核心操作

堆的强大之处在于它能高效地进行插入和删除（特指删除堆顶）操作，同时保持其"堆"的性质。为了维护这个性质，我们有两个基本操作：上浮和下沉。

5.1、插入元素

插入一个新元素时，为了不破坏完全二叉树的结构，我们遵循两步走策略：

将新元素放到数组的末尾。
对这个新元素执行 "上浮" 操作，直到它找到合适的位置。

下面我们来看一个最小堆具体插入示例：

初始状态：数组 [10, 20, 15, 30]

步骤1: 将 8 放在数组末尾。此时结构是完全二叉树，但堆序性被破坏 (8 < 20)。

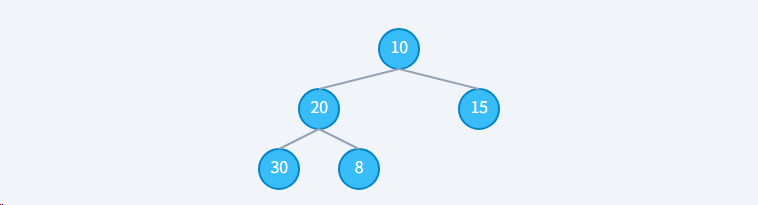
步骤2: 执行"上浮"8 (子) < 20 (父)，不满足最小堆性质，交换它们。

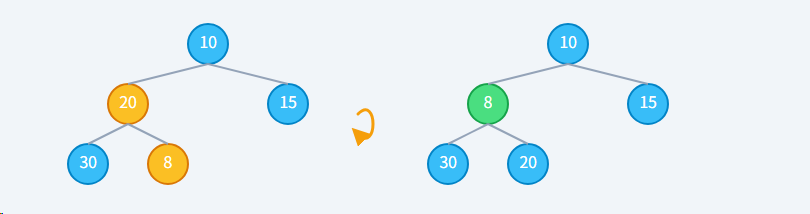
步骤3: 继续上浮 8 (子) < 10 (父)，仍然不满足，继续交换。

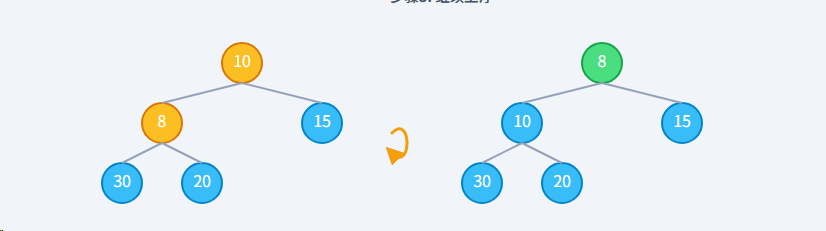
最终状态：上浮结束8 到达堆顶，它的父节点不存在了，或者它不再小于父节点，上浮停止。堆序性恢复。

5.2、删除元素

我们通常只关心堆顶的元素（最大或最小值）。删除它是一个精巧的过程：

用数组末尾的元素替换堆顶元素。
删除数组末尾的元素（此时它是重复的）。
对新的堆顶元素执行 "下沉" 操作，直到它找到合适的位置。

下面我们来看一个最小堆具体删除示例：

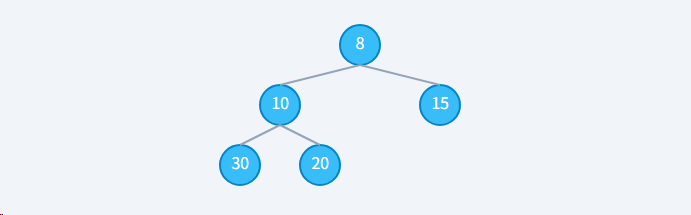
初始状态：数组 [8，10, 20, 15, 30]，删除8

步骤1: 用末尾的 20 替换堆顶的 8，然后"删除"末尾的 20。此时堆序性被破坏 (20 > 10, 20 > 15)。

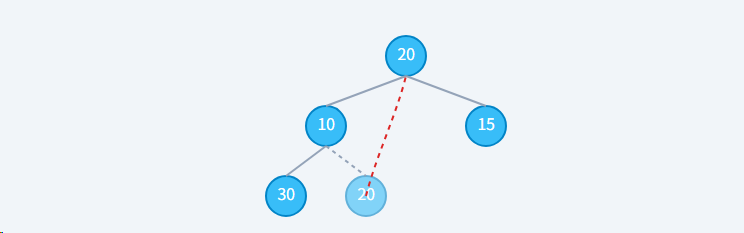步骤2: 执行"下沉"20 (父) 与它的子节点 (10, 15) 中较小的一个 (10) 比较。因为 20 > 10，不满足最小堆性质，交换它们。

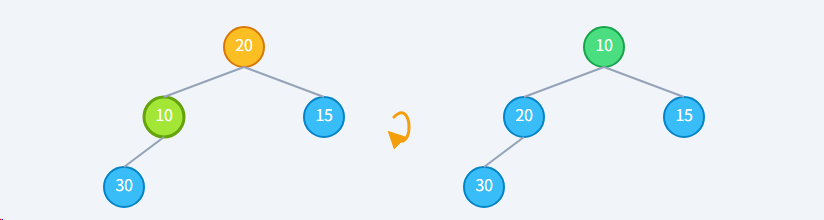
**步骤3: 继续下沉，**20 到达新位置，它没有子节点了，下沉结束。堆序性恢复。

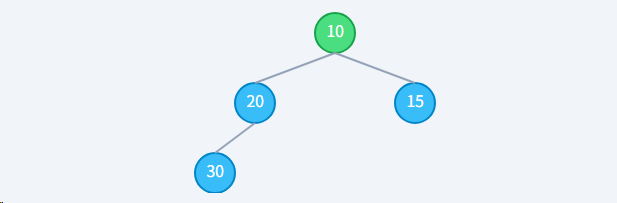
思考一个问题，为什么删除堆顶时，要用"末尾元素"去替换，而不是别的？

维护结构： 首要目标是不能破坏"完全二叉树"的结构。如果随意拿一个中间节点来替换，树就会出现"空洞"，数组也就不连续了，索引关系将全部失效。而拿走末尾元素是唯一不会在中间产生空洞的操作。
最小化调整： 将末尾元素放到堆顶，虽然大概率会破坏堆序性，但结构依然是完整的。我们只需要通过一次"下沉"操作（最多移动 log N 次）就能修复它。这种"先破坏再修复"的策略，在保证结构完整性的前提下，是效率最高的修复方式。

5.3、建堆

如果我们拿到一个无序的数组，如何将它转换成一个堆？这个过程就叫做"建堆"。

方法一：逐个插入 (效率较低)

最直观的方法是，创建一个空堆，然后遍历数组，将每个元素依次 insert 进堆里。每次插入的复杂度是 O(log N)，总共 N 个元素，所以总时间复杂度是 O(N log N)。

方法二：原地建堆 (更高效)

这是一个更高效的方法，时间复杂度仅为 O(N)。它的思想是"自下而上"地进行调整：

找到数组中最后一个非叶子节点。
从这个节点开始，向前遍历到根节点（索引0）。
对遍历到的每一个节点执行 "下沉" 操作。

为什么从"最后一个非叶子节点"开始，并且是"向前"遍历？

这正是该算法 O(N) 效率的关键所在！

为什么从最后一个非叶子节点开始？ 因为所有的叶子节点，它们自身都可以被看作是一个只包含一个元素的、已经满足堆序性的"迷你堆"。对它们执行下沉操作是毫无意义的。最后一个非叶子节点的索引可以通过 (数组长度 // 2) - 1 找到。
为什么要向前（自下而上）？ "下沉"操作有一个重要的前提：当对节点 i 执行下沉时，必须保证它的左右子树已经是合法的堆。通过从后向前遍历，当我们处理一个节点时，它的所有子孙节点都已经被处理过了，从而满足了下沉操作的前提。我们像搭积木一样，先把小堆（底层）弄好，再逐步合并成一个大堆。

示例

我们对数组 [3, 20, 10, 15, 8] 执行原地建堆 (最小堆)

初始状态: 一个无序数组，但结构上是完全二叉树

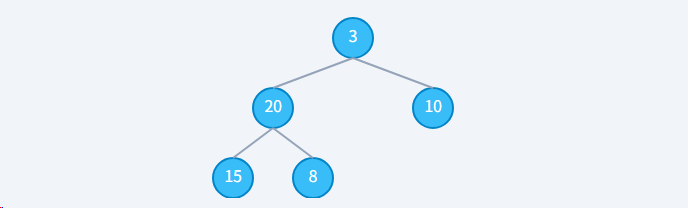
最后一个非叶子节点是索引为 (5 // 2) - 1 = 1 的节点 (值为20)。

**步骤1: 处理索引 1 (值 20)**对 20 执行下沉。20 > 8 (较小子节点)，交换。

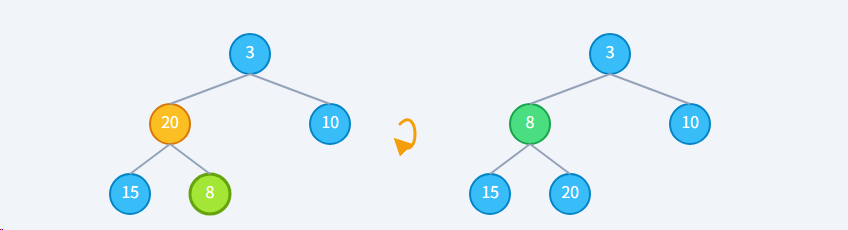
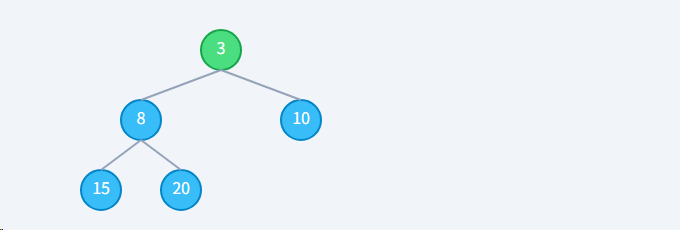
**步骤2: 处理索引 0 (值 3)**对 3 执行下沉。3 < 8 且 3 < 10，无需交换。

6、时间复杂度分析

操作	时间复杂度	说明
获取最大值	O(1)	直接返回根节点
插入元素	O(log n)	最多上浮 h 层
删除最大值	O(log n)	最多下沉 h 层
建堆	O(n)	自底向上算法

7、Python代码实现

下面是一个最小堆的Python实现

python 复制代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


class MinHeap:
    def __init__(self, array=None):
        # 如果提供了数组，就地建堆
        if array:
            self.heap = array
            self.heapify()
        else:
            self.heap = []

    def _get_parent_index(self, i):
        return (i - 1) // 2

    def _get_left_child_index(self, i):
        return 2 * i + 1

    def _get_right_child_index(self, i):
        return 2 * i + 2

    def _swap(self, i, j):
        self.heap[i], self.heap[j] = self.heap[j], self.heap[i]

    def _sift_up(self, i):
        parent_index = self._get_parent_index(i)
        while i > 0 and self.heap[i] < self.heap[parent_index]:
            self._swap(i, parent_index)
            i = parent_index
            parent_index = self._get_parent_index(i)

    def insert(self, value):
        self.heap.append(value)
        self._sift_up(len(self.heap) - 1)
        print(f"插入 {value} 后, 堆为: {self.heap}")

    def _sift_down(self, i):
        min_index = i
        size = len(self.heap)
        
        while True:
            left_child_index = self._get_left_child_index(i)
            right_child_index = self._get_right_child_index(i)
            
            # 找出当前节点和它的左右子节点中最小的那个
            if left_child_index < size and self.heap[left_child_index] < self.heap[min_index]:
                min_index = left_child_index
            
            if right_child_index < size and self.heap[right_child_index] < self.heap[min_index]:
                min_index = right_child_index
            
            if i == min_index:
                break
            
            self._swap(i, min_index)
            i = min_index

    def heapify(self):
        # O(N) 的建堆方法
        if not self.heap:
            return
        
        # 从最后一个非叶子节点开始，向前遍历并执行下沉
        last_non_leaf_index = (len(self.heap) // 2) - 1
        for i in range(last_non_leaf_index, -1, -1):
            self._sift_down(i)
        print(f"建堆后, 堆为: {self.heap}")

    def extract_min(self):
        if not self.heap:
            return None
        
        size = len(self.heap)
        if size == 1:
            return self.heap.pop()

        min_value = self.heap[0]
        self.heap[0] = self.heap.pop()
        self._sift_down(0)
        
        print(f"删除堆顶 {min_value} 后, 堆为: {self.heap}")
        return min_value


if __name__ == "__main__":
# --- 使用示例 ---
    print("--- 逐个插入建堆 ---")
    heap1 = MinHeap()
    heap1.insert(3)
    heap1.insert(20)
    heap1.insert(10)
    heap1.insert(15)
    heap1.insert(8)


    print("\n" + "-" * 20)
    print("--- 原地建堆 (Heapify) ---")
    unordered_array = [3, 20, 10, 15, 8]
    print(f"原始数组: {unordered_array}")
    heap2 = MinHeap(unordered_array) # 初始化时直接建堆

    heap2.extract_min()


# --- 逐个插入建堆 ---
# 插入 3 后, 堆为: [3]
# 插入 20 后, 堆为: [3, 20]
# 插入 10 后, 堆为: [3, 20, 10]
# 插入 15 后, 堆为: [3, 15, 10, 20]
# 插入 8 后, 堆为: [3, 8, 10, 20, 15]

# --------------------
# --- 原地建堆 (Heapify) ---
# 原始数组: [3, 20, 10, 15, 8]
# 建堆后, 堆为: [3, 8, 10, 15, 20]
# 删除堆顶 3 后, 堆为: [8, 15, 10, 20]

:::warning

在实际工程中，我们通常直接使用 Python 内置的 **heapq** 模块。它有一个 heapq.heapify(list) 函数，可以在 O(N) 时间内将一个列表原地转换为小顶堆，其原理正是我们刚才讨论的高效建堆法。

:::

8、可视化演示

https://code.juejin.cn/pen/7563132038170034226?embed=true

9、堆的应用

堆的核心价值在于能以 O(log N) 的时间复杂度完成插入和删除，并以 O(1) 的时间复杂度获取最值。这使得它在很多场景下都非常有用：

优先队列: 这是堆最直接、最经典的应用。医院急诊室、操作系统任务调度等都用到了优先队列。
堆排序 : 一种高效的原地排序算法，时间复杂度为 O(N log N)。
Top K 问题: "从10亿个整数中找出最大的100个"。通过维护一个大小为 K 的小顶堆可以高效解决。
图算法: Dijkstra 算法和 Prim 算法中，使用堆来高效地找到下一个要访问的、距离最近的节点。

10、总结

特性	描述
定义	一个满足堆序性的完全二叉树，通常用数组实现。
类型	最大堆：父 ≥ 子 (堆顶最大) 最小堆：父 ≤ 子 (堆顶最小)
时间复杂度	获取最值: O(1), 插入: O(log N), 删除堆顶: O(log N), 建堆: O(N)
主要应用	优先队列、堆排序、Top K 问题、图算法优化等。