---关注作者,送A/B实验实战工具包
在 AB 实验的决策会议上,最让人头秃、也最容易引发"撕逼"的场景往往是这样的:
- 产品经理 满面红光地指着 PPT:"大家看,实验组的点击率 (CTR) 显著提升了 5%,P 值小于 0.05,策略非常成功,我建议全量上线!"
- 运营同学 皱着眉头打断:"等一下,虽然点的人多了,但客单价 掉了 2% 啊。我算了一下,总的 GMV 其实根本没变,甚至还微跌了一点。"
- 客服主管 在旁边补了一刀:"而且你们没发现吗?退货率还微涨了 0.5%,后台关于'货不对板'的投诉变多了。这个策略明显在误导用户,长期看是在透支品牌。"
面对这种**"有涨有跌、互相打架"**的指标现场,到底该听谁的?
是听职级最高的?听嗓门最大的?还是谁背的 KPI 重就听谁的?
如果实验决策依赖于这种"人为博弈",那么 AB 实验就失去了它的客观性,变成了一种政治工具。
这时候,我们需要一个绝对理性的"最高法院"来做终审判决。这个机制就是 OEC (Overall Evaluation Criterion) ,即综合评估标准。
OEC 这个概念最早由微软在实验圣经《关键迭代》中提出。它不是某个单一的指标(如 GMV),而是一套将多个互相冲突的指标转化为单一决策信号的数学逻辑。它是实验决策从"玄学"走向"科学"的分水岭。
1. 初级阶段:加权得分法 (Weighted Score)
这是最容易落地、也是最直观的方法。它的核心逻辑非常简单:上帝归上帝,凯撒归凯撒,权重归老板。
既然指标之间有冲突,那我们就把业务关注的所有核心指标列出来,根据公司当前的战略重点,给每个指标分配一个"权重系数"。最后,将所有指标的实验收益加权求和,算出一个唯一的"综合得分"。
实战案例:电商大促推荐算法
假设我们正在测试一个新的首页推荐算法。实验跑了一周,数据如下:
- 正向指标 :
- GMV:涨了 5%。这是公司今年的核心 KPI,权重最高。
- 点击率 (CTR):涨了 10%。这代表用户兴趣度,权重次之。
- 负向指标 :
- 退货率:涨了 20%。这是必须压制的体验指标,权重为负。
OEC 公式设计 :
我们可以构建如下的线性公式:
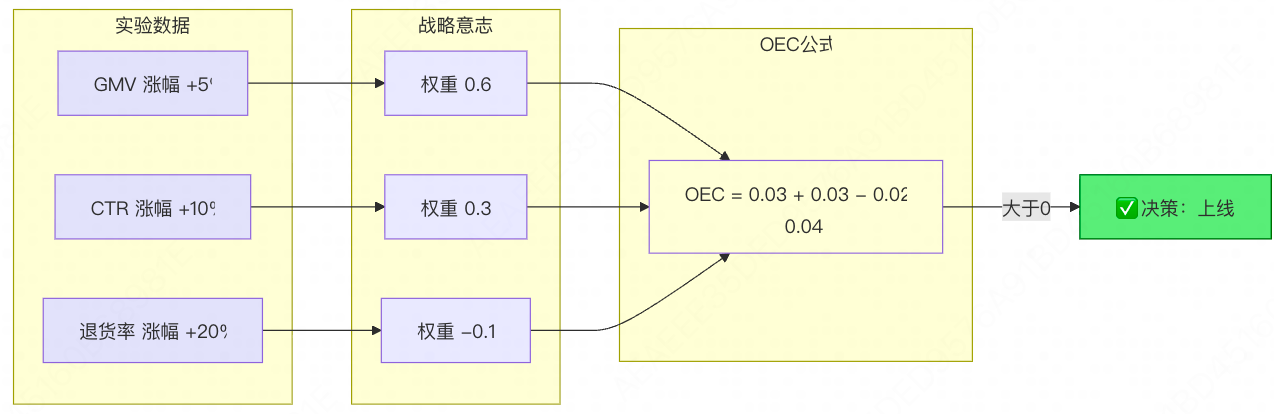
OEC = 0.6 × Lift(GMV) + 0.3 × Lift(CTR) − 0.1 × Lift(Return) \text{OEC} = 0.6 \times \text{Lift(GMV)} + 0.3 \times \text{Lift(CTR)} - 0.1 \times \text{Lift(Return)} OEC=0.6×Lift(GMV)+0.3×Lift(CTR)−0.1×Lift(Return)
- Lift:指实验组相对于对照组的涨幅百分比(例如 +0.05)。
- 权重逻辑 :
- GMV 最重要,给 0.6。
- CTR 是过程指标,给 0.3。
- 退货率是负向的,给 -0.1(注意这里是减号,意味着退货率涨得越多,得分越低)。
决策计算 :
OEC = 0.6 × 0.05 + 0.3 × 0.10 − 0.1 × 0.20 \text{OEC} = 0.6 \times 0.05 + 0.3 \times 0.10 - 0.1 \times 0.20 OEC=0.6×0.05+0.3×0.10−0.1×0.20
OEC = 0.03 + 0.03 − 0.02 = 0.04 \text{OEC} = 0.03 + 0.03 - 0.02 = 0.04 OEC=0.03+0.03−0.02=0.04
最终判决 :
因为 OEC = 0.04 > 0 ,说明虽然退货率涨了,但 GMV 和点击率带来的正向收益足够大,完全覆盖了退货带来的负面损失。
结论:策略通过,建议上线。
示意图:
2. 高级阶段:经济模型法 (Economic Model)
加权得分法虽然好用,但有一个明显的硬伤:权重是谁定的?
为什么 GMV 的权重是 0.6 而不是 0.5?为什么退货率的惩罚系数是 -0.1 而不是 -0.2?如果老板心情变了,权重是不是也要变?
为了消除这种"拍脑袋"的主观性,更科学、更硬核的方法是**"一切向钱看"**。
这就是经济模型法 。我们将所有的指标------无论是点击、关注,还是退货、投诉------都通过数据模型折算成真金白银(货币价值) 。这样,OEC 就变成了一个纯粹的财务公式:预期综合损益。
实战案例:亚马逊邮件广告
场景:亚马逊营销团队想给用户多发一封"猜你喜欢"的营销邮件。
- 短期收益:用户点了邮件里的商品,产生了直接购买收入。这是显而易见的。
- 长期损失:用户觉得这封邮件是垃圾骚扰,点击了底部的"取消订阅"。这意味着我们永远失去了通过邮件联系该用户的机会,这个损失是隐形且巨大的。
OEC 公式设计 :
我们需要构建一个公式,来衡量"发这封邮件"到底赚不赚钱:
OEC = 短期营收 − ( 退订人数 × 用户生命周期价值损失 ) \text{OEC} = \text{短期营收} - (\text{退订人数} \times \text{用户生命周期价值损失}) OEC=短期营收−(退订人数×用户生命周期价值损失)
参数估算:
- 短期营收 :假设实验数据显示,每多发一封邮件,平均能带来 $0.1 的新增 GMV。
- 长期损失 :通过历史数据分析(LTV 模型),我们算出一个活跃订阅用户的生命周期价值是 1000。如果他退订了,我们只能通过其他昂贵渠道(如广告)触达他,导致利润损失 **20**。
决策红线 :
OEC = 0.1 − ( 退订率 × 20 ) \text{OEC} = 0.1 - (\text{退订率} \times 20) OEC=0.1−(退订率×20)
只有当 OEC > 0 时,策略才成立。
这意味着,如果这封邮件导致超过 0.5% ( 0.1 / 20 0.1 / 20 0.1/20) 的用户退订,哪怕它带来了再多的短期 GMV,也是亏本买卖,必须下线。
价值 :
这种方法极其精准,它直接回答了"为了赚眼前的 1 块钱,我们愿意牺牲多少用户体验"这个灵魂拷问,让决策变得无可辩驳。
3. 起步阶段:启发式决策 (Heuristics)
看到这里,你可能会说:"我们团队刚起步,没有足够的数据去算 LTV,也没有复杂的归因模型,甚至连权重都还没吵清楚,怎么办?"
别急,在没有公式之前,我们可以使用一套简单的**"四象限决策法"。这是一套基于经验的启发式规则**,虽然粗糙,但足以应对 80% 的日常决策。
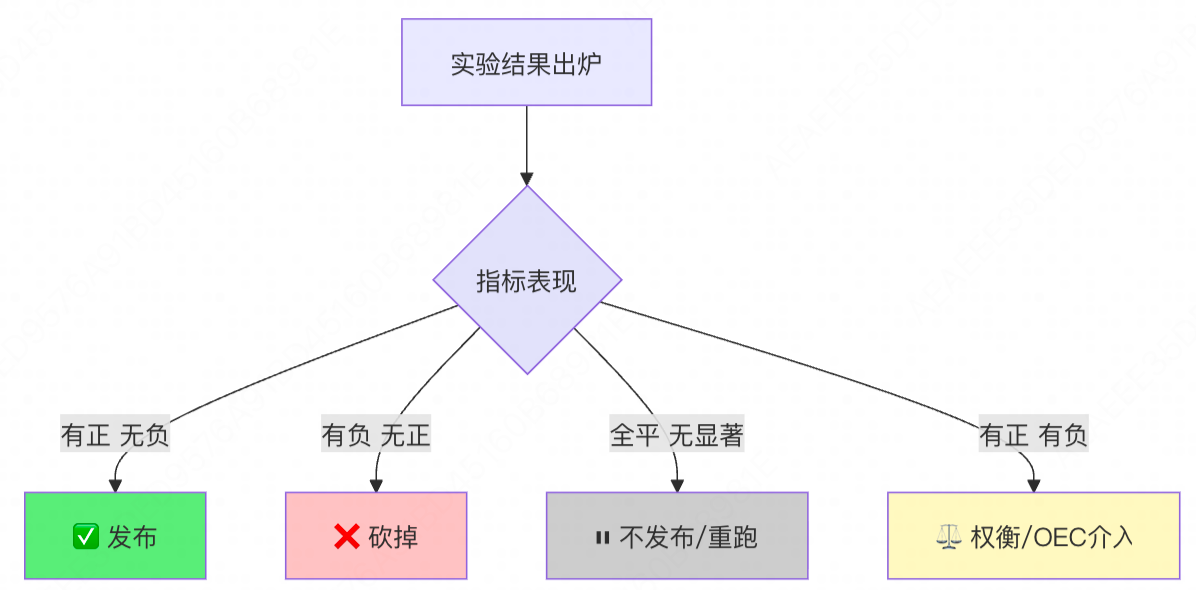
我们将所有关键指标分为三类状态:显著正向 、显著负向 、不显著(平)。
场景 1:皆大欢喜 (Positive + Flat)
- 现象:核心指标(如 GMV)显著涨了,其他指标(如退货率、延迟)没变化(统计不显著)。
- 决策 :发布 (Launch)。
- 逻辑:这是最完美的实验,纯收益,无副作用。不需要犹豫,直接推全。
场景 2:有毒策略 (Negative + Flat)
- 现象:核心指标显著跌了,或者护栏指标(如 App 崩溃率、卸载率)显著跌了,而其他指标没变化。
- 决策 :不发布 (Don't Launch)。
- 逻辑:只要有显著的负向影响,且没有巨大的正向对冲,一律视为"有毒"。不要幻想"可能只是波动",保护用户体验是第一位的。
场景 3:无效折腾 (All Flat)
- 现象:所有关键指标都是"平"的(统计不显著,置信区间跨过了 0)。
- 决策 :不发布 (Don't Launch)。
- 逻辑 :
- 成本视角:任何代码上线都有维护成本、技术债务和回滚风险。如果没有明确的收益,为什么要增加系统的复杂度?
- 统计视角:如果全平,可能是样本量不足(Power 不够)。建议考虑增加流量重跑,或者直接承认该方向无效,换个方向尝试。
场景 4:艰难权衡 (Mixed)
- 现象:有的指标显著涨(GMV +5%),有的指标显著跌(退货率 +2%)。
- 决策 :进入"人工议事会"。
- 逻辑 :
- 这是最纠结的时刻,也是最需要 OEC 的时刻。
- 在没有公式前,先基于简单的**"止损原则"**:如果负向指标触碰了底线(如退货率 > 30%),直接否决。
- 随着这种"纠结"案例的积累,你会慢慢摸索出"1% 的退货率到底值多少 GMV",从而进化到第 1 阶段(加权得分法)。
总结
OEC 的本质,是将**"多维度的纠结"降维成"一维度的数值"**。它不是一蹴而就的,而是随着业务成熟度不断进化的:
- 起步期:用"四象限法"快速过滤明显的好坏策略,解决 80% 的简单决策。
- 发展期:引入"加权得分",让业务偏好数字化,解决指标打架的问题。
- 成熟期:构建"经济模型",让实验直接对财务报表负责,实现真正的 ROI 最大化。
没有完美的 OEC,只有最适合当前业务阶段的 OEC。
如果这篇文章帮你理清了思路,不妨点个关注,我会持续分享 AB 实验干货文章。
