AI 的“诚实”指南：一文详解 Conformal Prediction (共形预测) 与 Split Conformal

AI 的"诚实"指南：一文详解 Conformal Prediction (共形预测) 与 Split Conformal

摘要：在 AI 落地的高风险领域，"大概率是对的"往往意味着"有概率会发生灾难"。如何让黑盒模型（Deep Learning）诚实地表达自己的"无知"？

本文基于顶刊综述 Theoretical Foundations of Conformal Prediction ，以"像素级"的颗粒度，深度拆解 Conformal Prediction (CP) 的数学基石。我们将从**可交换性（Exchangeability）**出发，推导 Split Conformal 与 Full Conformal 的算法本质，并结合论文核心图表，深入探讨如何构建自适应的预测区间。

关键词：Conformal Prediction, Split Conformal, 假设检验, 可交换性, 不确定性量化

1. 绪论：为什么我们需要"严谨的"不确定性？

在传统的机器学习任务中，模型通常输出一个点预测 (Point Prediction)。

f ( x ) = "Cat" f(x) = \text{"Cat"} f(x)="Cat"
f ( x ) = 24.5 f(x) = 24.5 f(x)=24.5

然而，这种预测方式掩盖了风险。当数据分布发生偏移，或者输入样本位于高维空间的稀疏区域时，模型往往会给出错误但置信度极高的预测（Overconfident）。

Conformal Prediction (CP) 提供了一种通用的、统计学严谨的框架，它将点预测转化为集合预测 (Set Prediction) C ( X ) \mathcal{C}(X) C(X)，并提供如下保证：

P ( Y n + 1 ∈ C ( X n + 1 ) ) ≥ 1 − α \mathbb{P}(Y_{n+1} \in \mathcal{C}(X_{n+1})) \ge 1 - \alpha P(Yn+1∈C(Xn+1))≥1−α

这个公式看似简单，但其背后的含金量极高：

有限样本保证 (Finite-sample Guarantee) ：不需要 n → ∞ n \to \infty n→∞，哪怕只有 50 个数据，保证依然成立。
无分布假设 (Distribution-free)：不需要假设数据服从高斯分布或拉普拉斯分布。
模型无关 (Model-agnostic)：无论是线性回归还是 Transformer，都可以"外挂"这个模块。

2. 数学基石：可交换性 (Exchangeability)

要理解 CP 为什么有效，必须先理解它的唯一假设：数据的可交换性。这是原论文花大篇幅讲解的基础。

2.1 什么是可交换性？

假设我们有一组随机变量 Z 1 , Z 2 , ... , Z n Z_1, Z_2, \dots, Z_n Z1,Z2,...,Zn（其中 Z i = ( X i , Y i ) Z_i = (X_i, Y_i) Zi=(Xi,Yi)）。如果我们要对这一组变量的联合分布进行全排列，而排列后的联合概率分布保持不变，那么这组变量就是可交换的。

通俗地说，数据的顺序不重要 。

最常见的可交换数据就是 i.i.d. (独立同分布) 数据。但可交换性的范围比 i.i.d. 更广（例如无放回抽样也是可交换的）。

2.2 秩的均匀分布 (Uniformity of Ranks)

这是 CP 的核心魔法 。

如果数据 Z 1 , ... , Z n + 1 Z_1, \dots, Z_{n+1} Z1,...,Zn+1 是可交换的，并且我们有一个评分函数 S ( Z ) S(Z) S(Z)（衡量误差大小），那么分数 S 1 , ... , S n + 1 S_1, \dots, S_{n+1} S1,...,Sn+1 也是可交换的。

这就意味着，对于新的测试点 Z n + 1 Z_{n+1} Zn+1，它的分数 S n + 1 S_{n+1} Sn+1 在所有 n + 1 n+1 n+1 个分数中，排在第 1 名、第 2 名、...、第 n + 1 n+1 n+1 名的概率是完全相等的！

P ( Rank ( S n + 1 ) = k ) = 1 n + 1 , ∀ k ∈ { 1 , ... , n + 1 } \mathbb{P}(\text{Rank}(S_{n+1}) = k) = \frac{1}{n+1}, \quad \forall k \in \{1, \dots, n+1\} P(Rank(Sn+1)=k)=n+11,∀k∈{1,...,n+1}

正是基于这个性质，我们才能断定：新的测试数据的误差，有 90 % 90\% 90% 的概率会小于历史上 90 % 90\% 90% 的误差。 所有的 CP 算法都是在利用这个性质找"分位数"。

3. Split Conformal Prediction (SCP)：工业界的标准答案

Full Conformal 虽然理论优美，但在计算上极其昂贵（下文详述）。工业界 99% 的场景使用的是 Split Conformal Prediction（也称 Inductive Conformal）。

3.1 算法流程的数学描述

我们将数据集 D \mathcal{D} D 划分为训练集 D t r a i n \mathcal{D}{train} Dtrain 和校准集 D c a l \mathcal{D}{cal} Dcal（大小为 n n n）。

训练 (Training) ：

利用 D t r a i n \mathcal{D}_{train} Dtrain 训练模型 f ^ \hat{f} f^。此后 f ^ \hat{f} f^ 不再改变，视为固定函数。
计算校准分数 (Calibration Scores) ：

对于 D c a l \mathcal{D}_{cal} Dcal 中的每个样本 i = 1 , ... , n i=1, \dots, n i=1,...,n，计算非一致性分数 (Non-conformity Score)：
S i = s ( X i , Y i ) S_i = s(X_i, Y_i) Si=s(Xi,Yi)

最基础的定义是 S i = ∣ Y i − f ^ ( X i ) ∣ S_i = |Y_i - \hat{f}(X_i)| Si=∣Yi−f^(Xi)∣。
计算分位数 (Quantile) ：

我们需要找到一个阈值 q ^ \hat{q} q^，使得未来的分数 S n + 1 S_{n+1} Sn+1 有 1 − α 1-\alpha 1−α 的概率小于它。

根据可交换性原理，这个阈值应当是 S 1 , ... , S n S_1, \dots, S_n S1,...,Sn 中的第 ⌈ ( n + 1 ) ( 1 − α ) ⌉ \lceil (n+1)(1-\alpha) \rceil ⌈(n+1)(1−α)⌉ 小的值。

注意：很多教程简单地说是 1 − α 1-\alpha 1−α 分位数，但严谨的数学定义必须包含那个 + 1 +1 +1（代表未来的测试点）。

q ^ = Quantile ( S 1 , ... , S n ; ⌈ ( n + 1 ) ( 1 − α ) ⌉ n ) \hat{q} = \text{Quantile}(S_1, \dots, S_n; \frac{\lceil (n+1)(1-\alpha) \rceil}{n}) q^=Quantile(S1,...,Sn;n⌈(n+1)(1−α)⌉)
构建预测集 (Prediction Set) ：
C ( X n + 1 ) = { y ∣ s ( X n + 1 , y ) ≤ q ^ } \mathcal{C}(X_{n+1}) = \{ y \mid s(X_{n+1}, y) \le \hat{q} \} C(Xn+1)={y∣s(Xn+1,y)≤q^}

如果是回归问题且使用绝对残差分数，区间即为 [ f ^ ( X n + 1 ) − q ^ , f ^ ( X n + 1 ) + q ^ ] [\hat{f}(X_{n+1}) - \hat{q}, \ \hat{f}(X_{n+1}) + \hat{q}] [f^(Xn+1)−q^, f^(Xn+1)+q^]。

4. 深度图解：分数函数的进化 (Score Functions)

Score Function ( s ( x , y ) s(x,y) s(x,y)) 决定了预测区间的形状和质量。论文中的 Figure 1.1 展示了三种不同分数函数在异方差（Heteroscedasticity）数据上的表现。

Figure 1.1 深度解析
(请对照原论文 Figure 1.1 查看)

第一阶段：绝对残差 (Residual Score) - 左图

公式： s ( x , y ) = ∣ y − f ^ ( x ) ∣ s(x,y) = |y - \hat{f}(x)| s(x,y)=∣y−f^(x)∣
形态：生成的预测带是等宽的。
缺陷分析 ：
- 数据分布呈现"喇叭口"形状（右侧方差大）。
- 由于 q ^ \hat{q} q^ 是根据整体平均误差计算的，通过固定宽度覆盖 90% 的点。
- 结果：在左侧（低噪声区），区间过宽，包含大量无效空间；在右侧（高噪声区），区间过窄，无法覆盖真实值。
结论：仅适用于同方差（Homoscedastic）数据。

第二阶段：标准化残差 (Scaled Residual Score) - 中图

公式： s ( x , y ) = ∣ y − f ^ ( x ) ∣ σ ^ ( x ) s(x,y) = \frac{|y - \hat{f}(x)|}{\hat{\sigma}(x)} s(x,y)=σ^(x)∣y−f^(x)∣
机制：我们需要训练第二个模型 σ ^ ( x ) \hat{\sigma}(x) σ^(x) 来预测残差的绝对值（即预测不确定性）。
形态：预测带呈现自适应宽度。
优势分析 ：
- 当 σ ^ ( x ) \hat{\sigma}(x) σ^(x) 预测该区域噪声大时，分母变大，为了保持 S i S_i Si 不变，分子必须允许更大的偏差，因此区间自动变宽。
- 图中清晰可见，区间在右侧变宽，完美包裹了发散的数据点；在左侧变窄，提高了精度。
结论：这是回归任务中最推荐的通用方法（Locally Adaptive）。

第三阶段：CQR (Conformalized Quantile Regression) - 右图

公式： s ( x , y ) = max ⁡ { q ^ α / 2 ( x ) − y , y − q ^ 1 − α / 2 ( x ) } s(x,y) = \max \{ \hat{q}{\alpha/2}(x) - y, \ y - \hat{q}{1-\alpha/2}(x) \} s(x,y)=max{q^α/2(x)−y, y−q^1−α/2(x)}
机制：利用分位数回归模型（Quantile Regression）直接预测上界 q ^ h i g h \hat{q}{high} q^high 和下界 q ^ l o w \hat{q}{low} q^low。
形态：预测带不仅宽度自适应，而且非对称。
优势分析 ：
- 如果数据分布本身就是偏斜的（比如只有正误差），CQR 能生成"上面宽、下面窄"的区间。
- CP 在这里的作用是"校准"：如果分位数回归预测得不准（覆盖率不够 90%），CP 会计算一个偏移量来扩大或缩小这个区间。
结论：SOTA 方法，信息效率最高。

5. 理论溯源：Full Conformal Prediction (FCP)

理解 FCP 是理解 CP 的必经之路。它的本质是将预测问题转化为假设检验问题。

5.1 算法逻辑：反向思维

对于测试点 X n + 1 X_{n+1} Xn+1，我们想知道哪个 y y y 是合理的。FCP 的思路是：
"对于每一个可能的 y y y，假设它是真的，看它是否会让数据变得'奇怪'？"

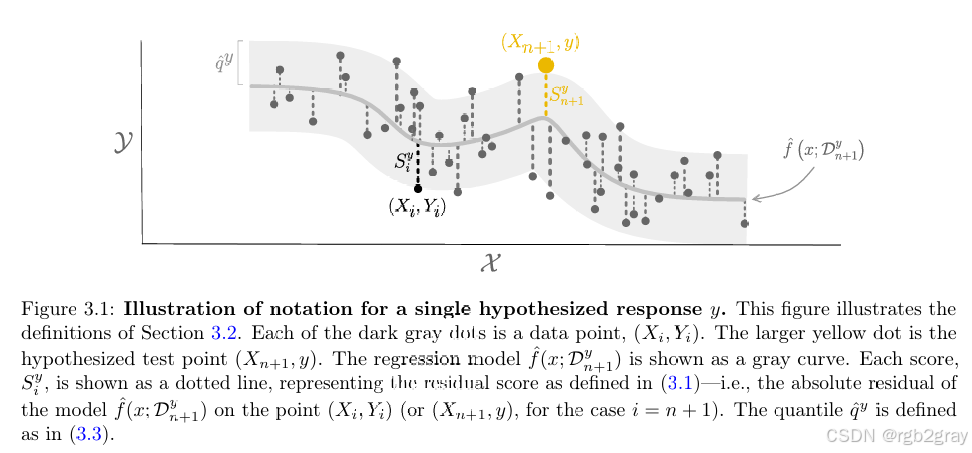
Figure 3.1 & 3.2 深度解析
(请对照原论文 Figure 3.1 和 3.2)

假设 (Hypothesize) ：

选取一个候选值 y ~ \tilde{y} y~。构建增广数据集 D ′ = D t r a i n ∪ { ( X n + 1 , y ~ ) } \mathcal{D}' = \mathcal{D}{train} \cup \{(X{n+1}, \tilde{y})\} D′=Dtrain∪{(Xn+1,y~)}。
重训练 (Retrain) ：

在 D ′ \mathcal{D}' D′ 上从头训练一个新的模型 f ^ y ~ \hat{f}_{\tilde{y}} f^y~。
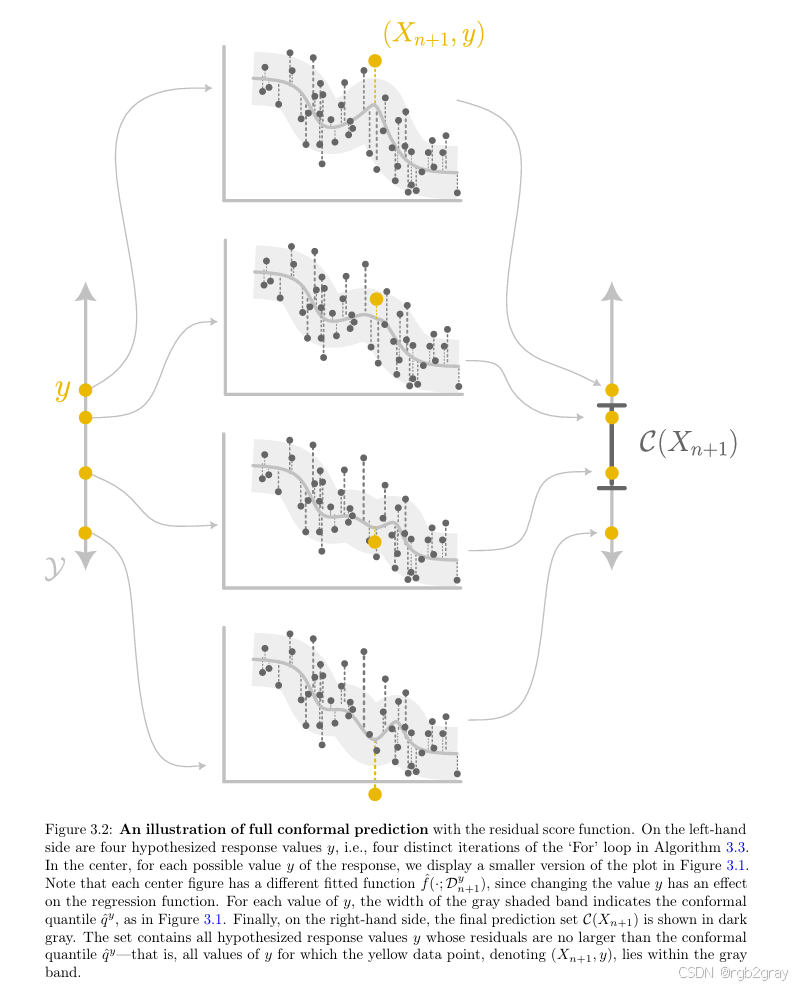
- 图解细节 ：在 Figure 3.2 中，你会看到随着假设 y ~ \tilde{y} y~ 的位置不同（从下到上扫描），中间拟合的灰色曲线形状也在发生微小的变化。这体现了测试点对模型的反向影响。
排序检验 (Rank Verification) ：

计算 D ′ \mathcal{D}' D′ 中所有点在新模型下的残差。

看 ( X n + 1 , y ~ ) (X_{n+1}, \tilde{y}) (Xn+1,y~) 的残差 S n + 1 S_{n+1} Sn+1 排在第几位。
- 如果 S n + 1 S_{n+1} Sn+1 特别大（排在最后），说明 y ~ \tilde{y} y~ 与现有数据分布不一致（Outlier），拒绝该假设。
- 如果 S n + 1 S_{n+1} Sn+1 处于中间位置，说明 y ~ \tilde{y} y~ 很合群，接受该假设。
求逆 (Inversion) ：

收集所有被"接受"的 y ~ \tilde{y} y~，它们组成的集合就是最终的预测区间 C ( X n + 1 ) \mathcal{C}(X_{n+1}) C(Xn+1)。

5.2 计算复杂度之殇

对于回归问题， y ~ \tilde{y} y~ 是连续变量，甚至有无穷多个。对于每一个 y ~ \tilde{y} y~ 都要重训模型，计算复杂度是 O ( ∞ ) O(\infty) O(∞)。

即便是分类问题，每次预测也要重训 K K K 次模型。

这就是为什么 FCP 理论完美，但除了线性回归等极少数场景（利用 Sherman-Morrison 公式快速更新参数）外，几乎无法直接使用的原因。

6. 避坑指南：边际覆盖 vs 条件覆盖

这是原论文反复强调的概念，也是新手最容易犯的错误。

CP 提供的 1 − α 1-\alpha 1−α 保证是边际的 (Marginal) 。
P ( Y ∈ C ( X ) ) ≥ 1 − α \mathbb{P}(Y \in \mathcal{C}(X)) \ge 1-\alpha P(Y∈C(X))≥1−α

这里的概率 P \mathbb{P} P 是对 X X X 和 Y Y Y 的联合分布求期望。通俗说，是"平均准确率"。

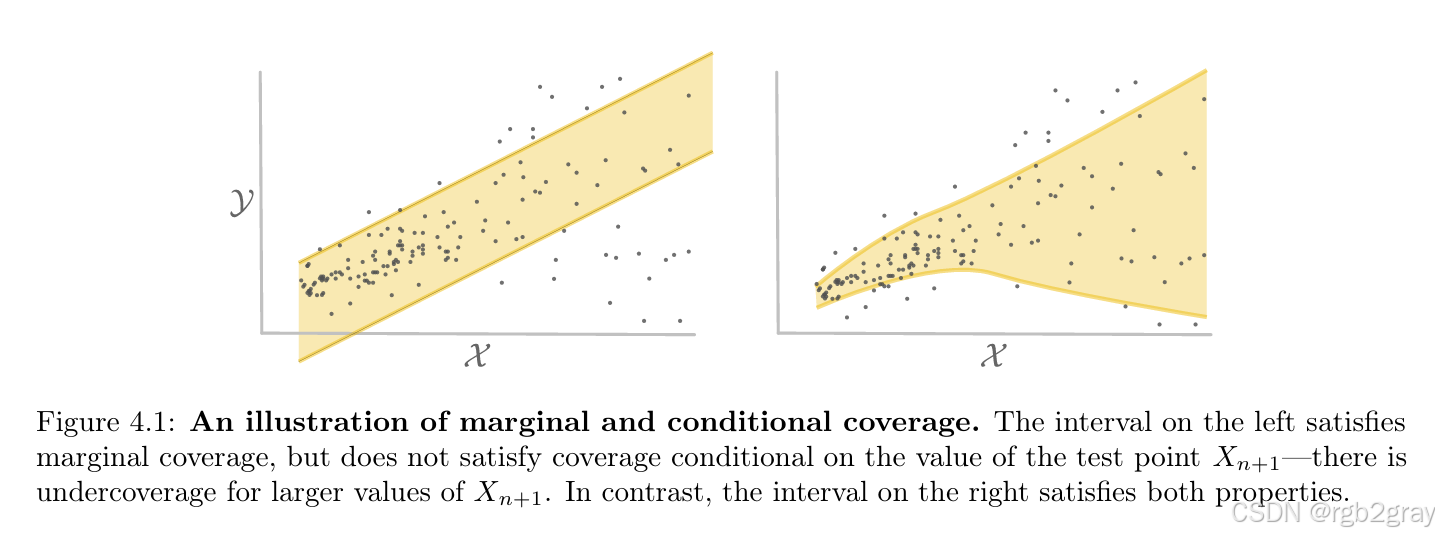
Figure 4.1 深度解析
(请对照原论文 Figure 4.1)

左图：边际覆盖 (Marginal Coverage)
- 统计整张图，红点落在灰色区间内的比例确实是 90%。
- 致命缺陷 ：观察 X > 5 X > 5 X>5 的区域（图右侧）。在这个子群体中，覆盖率几乎为 0%！
- 这意味着模型对某一类特定的样本（如特定的种族、特定的年龄段、特定的路况）完全失效，但在整体的高准确率掩护下，这个问题被隐藏了。
右图：条件覆盖 (Conditional Coverage)
- 目标： P ( Y ∈ C ( X ) ∣ X = x ) ≥ 1 − α \mathbb{P}(Y \in \mathcal{C}(X) \mid X=x) \ge 1-\alpha P(Y∈C(X)∣X=x)≥1−α。
- 这就是我们追求的理想状态：无论 X X X 取值如何，覆盖率都稳定在 90%。
- 虽然理论上证明了在有限样本下无法严格实现完美的条件覆盖，但通过使用自适应分数（如 CQR 或 Scaled Residual），我们可以逼近右图的效果。

7. 总结与实施建议

7.1 核心结论

点预测是不可靠的：必须构建预测区间来量化不确定性。
Split Conformal 是首选：既保留了统计保证，又极大地降低了计算量（只需训练一次）。
Score Function 决定成败 ：不要无脑使用 ∣ y − f ^ ( x ) ∣ |y-\hat{f}(x)| ∣y−f^(x)∣，尽量使用包含不确定性估计的标准化分数。

7.2 极简实现代码 (Python)

为了让你立刻上手，这里提供一个 SCP 的伪代码逻辑：

python 复制代码

import numpy as np

# 1. 数据切分
X_train, X_cal, y_train, y_cal = train_test_split(X, y, test_size=0.2)

# 2. 训练模型 (此处以分位数回归为例，模拟 CQR)
model.fit(X_train, y_train)

# 3. 计算校准分数
# 假设模型输出了 lower 和 upper 两个边界
preds_cal_low, preds_cal_high = model.predict(X_cal)
# CQR 分数公式：max(low - y, y - high)
scores = np.maximum(preds_cal_low - y_cal, y_cal - preds_cal_high)

# 4. 计算分位数 (关键一步)
alpha = 0.1 # 90% 覆盖率
n = len(y_cal)
q_level = np.ceil((n + 1) * (1 - alpha)) / n
q_hat = np.quantile(scores, q_level, method='higher')

# 5. 预测新数据
preds_new_low, preds_new_high = model.predict(X_new)
final_lower = preds_new_low - q_hat
final_upper = preds_new_high + q_hat