---关注作者,送A/B实验实战工具包
在设计 AB 实验时,我们经常会遇到这样的灵魂拷问:
"这个实验是按人 (User) 分流,还是按访问 (Session) 分流?"
"我按人分流了,最后能不能算点击率 (CTR) 的 P 值?"
这两个问题触及了实验设计的底层逻辑:分流单元 (Diverting Unit) 与 分析单元 (Analysis Unit) 的匹配关系。
如果这两个单元没对齐,轻则用户体验崩塌(同一个用户一会看到红按钮,一会看到绿按钮),重则统计结论失效(明明不显著却算出了显著)。
今天我们就来厘清这对"相爱相杀"的概念。
1. 粒度层级:俄罗斯套娃
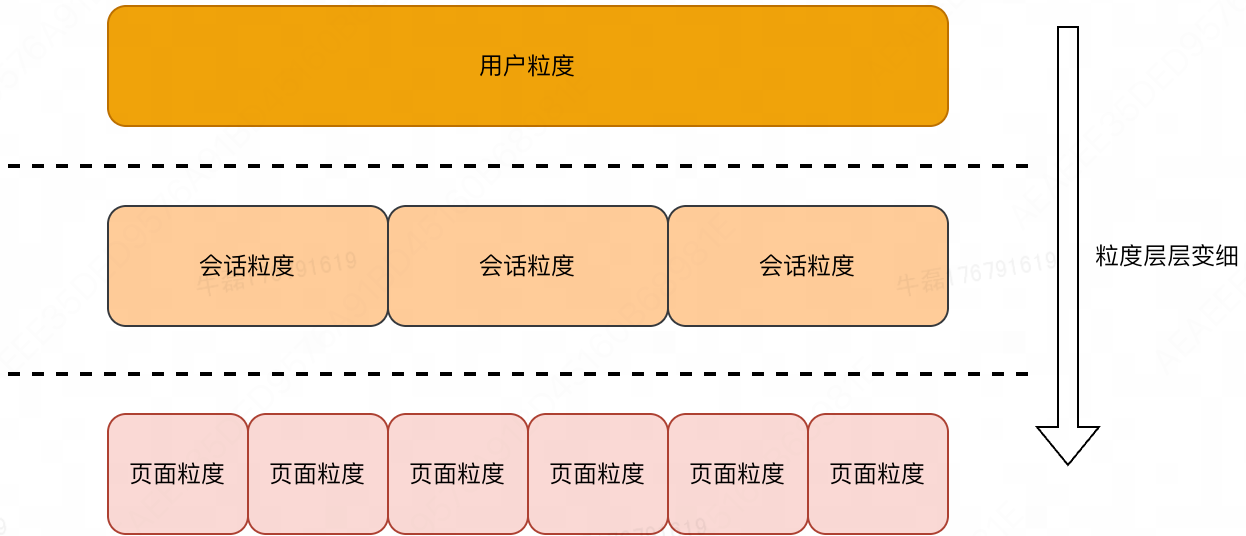
首先,我们要建立一个粒度 (Granularity) 的概念。在互联网数据中,粒度是像俄罗斯套娃一样层层嵌套的:
- 用户粒度 (User ID):最粗。一个用户对应唯一的 ID,包含他所有的生命周期行为。
- 会话粒度 (Session ID):中等。一个用户在一天内可能打开 App 5 次,产生 5 个 Session。
- 页面/请求粒度 (Pageview/Request ID):最细。一个 Session 内可能浏览了 10 个页面,产生 10 个 PV。
理解这个层级关系,是做对实验的前提。
 ---
---
2. 如何选择分流单元?------体验连贯性原则
分流单元 决定了"谁"进入实验组,"谁"进入对照组。选择的核心原则只有一条:保证用户体验的连贯性 (Consistency)。
场景 A:必须按用户分流 (User ID)
如果实验涉及视觉、交互、功能流程的改动,必须用 User ID。
- 例子:UI 改版(红按钮 vs 蓝按钮)。
- 逻辑:如果你按 PV 分流,用户刷新一下页面,按钮从红变蓝,再刷新又变红。用户会觉得 App 出 Bug 了,产生困惑和沮丧,导致流失。
场景 B:可以按会话/请求分流 (Session/Request ID)
如果实验改动是后端逻辑、算法、广告,且用户感知不强,可以用更细的粒度。
- 例子:搜索排序算法、广告出价策略。
- 逻辑:用户这次搜"苹果"出结果 A,下次搜"苹果"出结果 B,通常是可以接受的。
- 好处:粒度越细,样本量越大(PV 数远大于 UV 数),实验越容易显著,迭代越快。
3. 黄金定律:分流粒度 ≥ \ge ≥ 分析粒度
分析单元决定了我们在计算指标时,是以什么维度聚合数据的(分母是谁)。
- 算 DAU 、留存率 、ARPU → \rightarrow → 分析单元是 User。
- 算 点击率 (CTR) 、转化率 (CVR) → \rightarrow → 分析单元通常是 PV 或 Session。
在统计学上,为了保证 T 检验 有效,必须遵守一个铁律:
分流单元的粒度,必须粗于或等于分析单元的粒度。
Granularity(Diverting) ≥ Granularity(Analysis) \text{Granularity(Diverting)} \ge \text{Granularity(Analysis)} Granularity(Diverting)≥Granularity(Analysis)
我们来看看三种情况:
情况 1:完美匹配 (User Split → \rightarrow → User Metric)
- 分流:按 User ID。
- 指标:人均时长、留存率。
- 评价 :最标准。满足 IID(独立同分布)假设,直接算 P 值没问题。
情况 2:绝对禁区 (Session Split → \rightarrow → User Metric)
- 分流:按 Session ID(粒度细)。
- 指标:DAU、留存率(粒度粗)。
- 评价 :错误!严禁操作!
- 原因 :这直接破坏了 独立同分布 (i.i.d.) 的核心原则。
- 用户 Bob 有两个 Session。Session A 进了实验组,Session B 进了对照组。
- 在算 DAU 时,Bob 既给实验组贡献了 +1,又给对照组贡献了 +1。
- 两组数据不再独立,你的 T 检验前提崩塌,算出来的结论是垃圾。
- 延伸阅读 :关于独立同分布的重要性,强烈推荐阅读我的这篇博客:《AB实验的关键认知(二)独立同分布》,里面详细拆解了为什么它是实验的生死线。
情况 3:技术深水区 (User Split → \rightarrow → PV Metric)
- 分流:按 User ID(粒度粗)。
- 指标:点击率 CTR(分母是 PV,粒度细)。
- 评价 :允许,但要小心。
- 问题 :这属于"分流单元 > 分析单元"。虽然满足独立性(人与人独立),但方差计算变复杂了 。
- 同一个用户产生的 10 个 PV 是高度相关的(自相关性)。如果不处理这种相关性,直接把所有 PV 混在一起算 T 检验,会导致方差被低估,P 值虚低(容易假阳性)。
- 解法 :必须使用 Delta Method 或 Bootstrap 来校正方差。简单的 P = Z / p ( 1 − p ) / N P = Z / \sqrt{p(1-p)/N} P=Z/p(1−p)/N 公式在这里失效了。
总结:避坑指南
为了不把实验做废,请在设计阶段对着下表自查:
| 分流单元 (Diverting) | 分析指标 (Metric) | 分析单元 (Analysis) | 判定结果 | 备注 |
|---|---|---|---|---|
| User ID | 留存率、ARPU | User | ✅ 通过 | 标准做法 |
| User ID | 点击率 (CTR) | PV | ⚠️ 需校正 | 需用 Delta Method 估算方差 |
| Session ID | 点击率 (CTR) | Session/PV | ✅ 通过 | 适合算法/广告实验 |
| Session ID | 留存率、DAU | User | ❌ 禁止 | 违背独立性,指标无意义 |
一句话心法:你可以把一个人拆成很多次行为去分析,但绝不能把一个人的多次行为拆给不同的组。
如果这篇文章帮你理清了思路,不妨点个关注,我会持续分享 AB 实验干货文章。
