前言
欢迎进入第七章:控制系统的经典设计方法。
在经历了前六章的建模、分析和非线性仿真后,你已经从一名"观测者"进化为了"诊断师"。而从本章开始,你将正式成为一名**"设计师"**。
如果说前几章是在研究"这个病人的身体状况如何",那么第七章就是**"对症下药"。当系统的稳定性储备不足、反应太慢或者超调太大时,我们需要设计补偿器(Compensator)或反馈阵(Feedback Gain)来改造它。本章涵盖了从经典的 超前滞后校正到现代控制理论入门的 极点配置与最优控制(LQR)**。
我们将通过 MATLAB 的自动化设计工具和 Simulink 的结构化建模,手把手教你如何"医治"一个性能不合格的系统。
一、 核心原理与知识点汇总
- 串联校正(Lead/Lag):通过在主回路串联补偿环节,利用相位超前提高稳定性,利用相位滞后改善稳态精度。
- 极点配置(Pole Placement):针对状态空间模型,通过状态反馈将系统的闭环极点强制移动到你预设的"理想位置"。
- 最优控制(LQR):不再手动指定极点,而是定义一个"代价函数"(权衡误差和能量消耗),让 MATLAB 自动算出最完美的反馈增益。
- 多变量系统解耦:处理多个输入互相干扰的复杂系统,使其变成互不干涉的单回路。
二、 必会 MATLAB 函数清单
1. sisotool(sys) ------ 交互式设计万能工具箱
-
功能:打开一个集根轨迹、波特图、阶跃响应于一体的图形化界面,支持鼠标拖拽极点直接设计控制器。
-
输入 :受控对象模型
G。 -
代码示例 :
matlabG = tf(1, [1 1 0]); % 建立一个不稳定的积分环节 sisotool(G); % 讲解:执行后会弹出窗口。你可以直接在波特图上增加"Lead"环节,实时观察阶跃响应变快的过程。
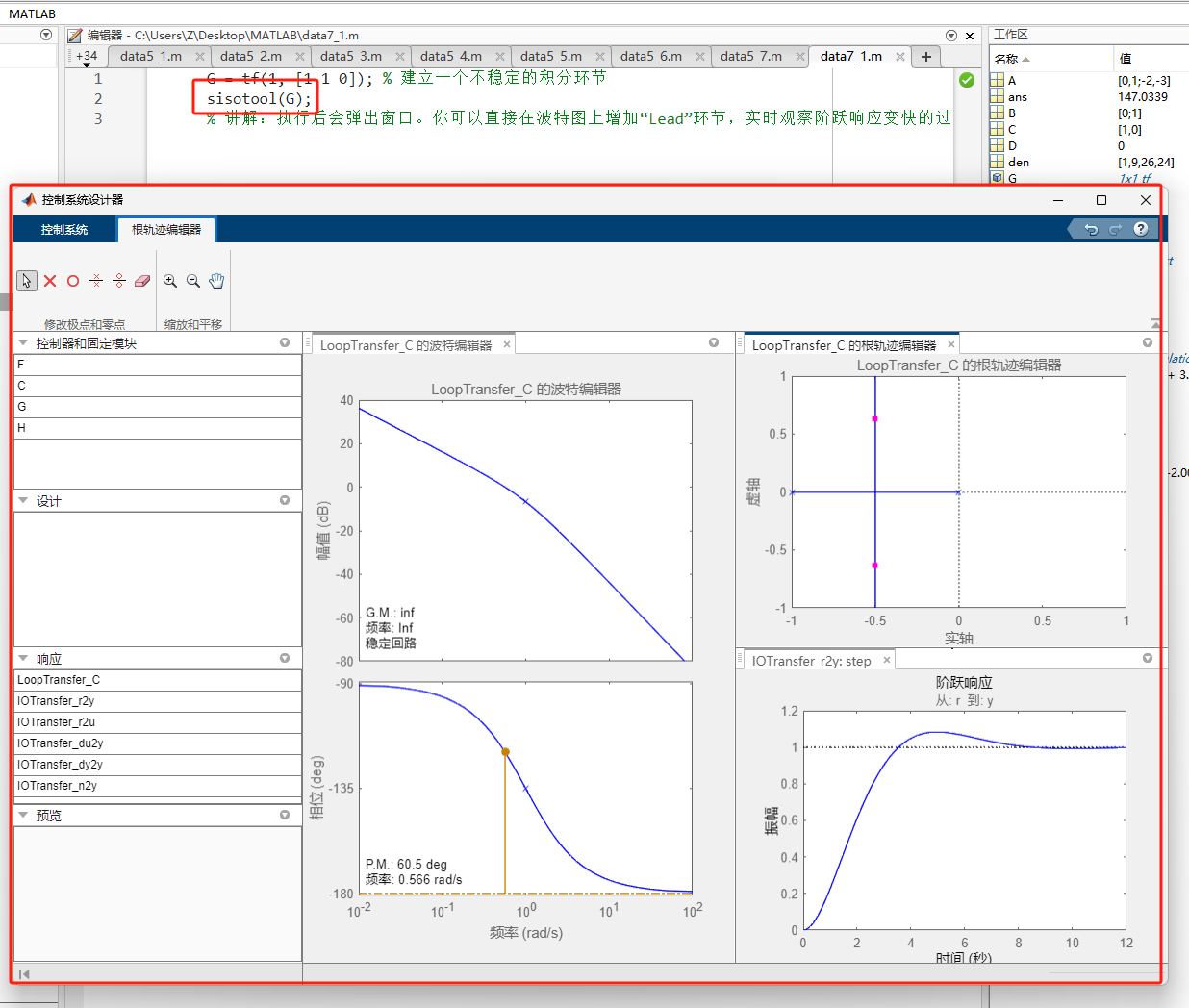
2. place(A, B, P) ------ 极点配置设计
-
功能 :计算状态反馈增益矩阵 KKK,使闭环系统 (A−BK)(A-BK)(A−BK) 的极点正好等于理想极点向量 PPP。
-
输入 :系统阵 AAA、输入阵 BBB、期望极点位置 PPP。
-
返回值 :反馈增益矩阵 KKK。
-
代码示例 :
matlabA = [0 1; -2 -3]; B = [0; 1]; P = [-2+2i, -2-2i]; % 我们希望系统具有阻尼比0.707的特性 K = place(A, B, P); disp('计算出的反馈增益 K:'); disp(K); % 讲解:这是现代控制理论的"上帝之手",只要系统可控,你可以让它具有任何你想要的动态特性。
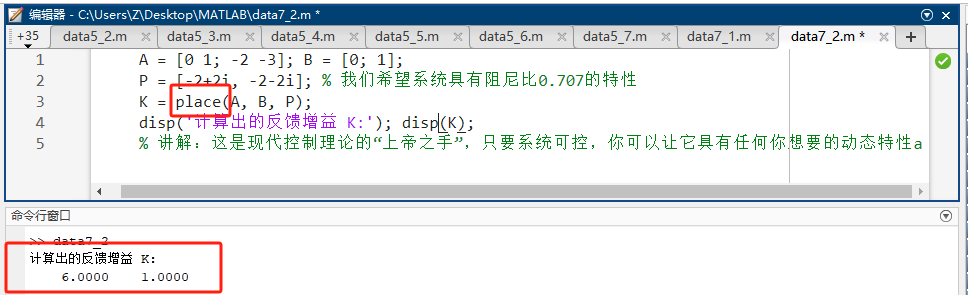
3. lqr(A, B, Q, R) ------ 线性二次型最优调节器
-
功能 :寻找最优反馈增益 KKK,使代价函数 J=∫(xTQx+uTRu)dtJ = \int (x^TQx + u^TRu) dtJ=∫(xTQx+uTRu)dt 最小。
-
输入 :系统参数 A,BA, BA,B,误差权重阵 QQQ,能量消耗权重阵 RRR。
-
返回值 :最优增益 KKK。
-
代码示例 :
matlabA = [0 1; -2 -3]; B = [0; 1]; Q = [100 0; 0 1]; % 高度重视位置误差 R = 1; % 对控制能量消耗要求一般 K_opt = lqr(A, B, Q, R); disp('最优增益 K_opt:'); disp(K_opt); % 讲解:Q越大,系统反应越快但越费电;R越大,系统越省电但反应越肉。LQR 帮你做平衡。
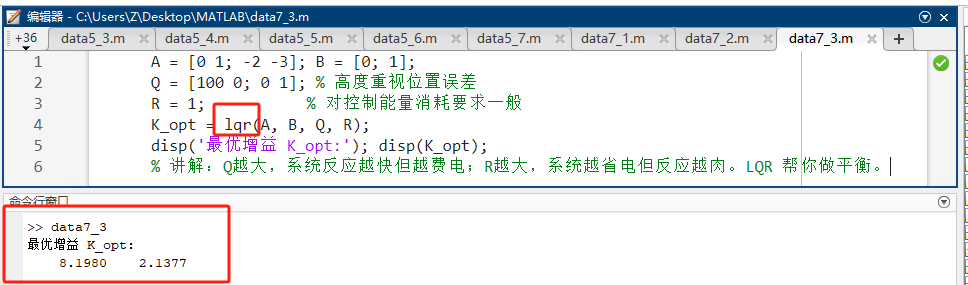
三、 必会 Simulink 模块详解
在第七章的设计验证中,以下模块是你的"实验台核心":
| 模块名称 | 所在库 | 功能讲解与用处 |
|---|---|---|
| Transfer Fcn (传递函数) | Continuous | 用处 :代表受控对象 G(s)G(s)G(s)。 |
| Zero-Pole (零极点) | Continuous | 用处 :输入形如 [0], [-1 -2], [10],适合直接放入你设计的校正环节。 |
| State-Space (状态空间) | Continuous | 用处 :验证状态反馈。双击填入 A-B*K 或使用外部输入反馈 u=−Kxu=-Kxu=−Kx。 |
| Matrix Gain (矩阵增益) | Math Operations | 用处 :将 Gain 模块的 Multiplication 属性设为 Matrix(K*u),用于实现 KxKxKx 反馈。 |
| Sum (求和) | Math Operations | 用处 :可以将符号改为 +- 以建立负反馈回路。 |
四、 阶段性综合实战 (Milestone 3)
项目:倒立摆平衡控制(简化版)
背景 :倒立摆是一个不稳定的系统。其线性化模型为:x˙=Ax+Bu\dot{x} = Ax + Bux˙=Ax+Bu,其中 A=[0,1;10,0],B=[0;1]A = [0, 1; 10, 0], B = [0; 1]A=[0,1;10,0],B=[0;1]。
任务:
- 计算该不稳定的开环极点。
- 使用
place函数设计状态反馈,使闭环极点位于 [−2,−2][-2, -2][−2,−2]。 - 在 Simulink 中搭建该反馈系统,验证初值响应(从倾斜恢复到垂直)。
MATLAB 设计脚本:
matlab
%% 1. 系统定义
%% 1. 系统定义
A = [0 1; 10 0]; % 10代表倒立摆的不稳定性
B = [0; 1];
C = [1 0]; D = 0;
poles_open = eig(A); % 结果包含 +3.16,说明系统会自动倒下
%% 2. 控制器设计 (极点配置)
P_des = [-2, -2]; % 期望闭环极点
K = acker(A, B, P_des);
fprintf('为了稳定倒立摆,需要的反馈增益 K = [%.2f, %.2f]\n', K(1), K(2));
%% 3. 闭环系统验证
sys_cl = ss(A - B*K, B, C, D);
t = 0:0.01:5;
initial(sys_cl, [0.1; 0]); % 给摆一个0.1弧度的初始偏差
title('倒立摆从0.1rad偏差恢复的过程');
grid on;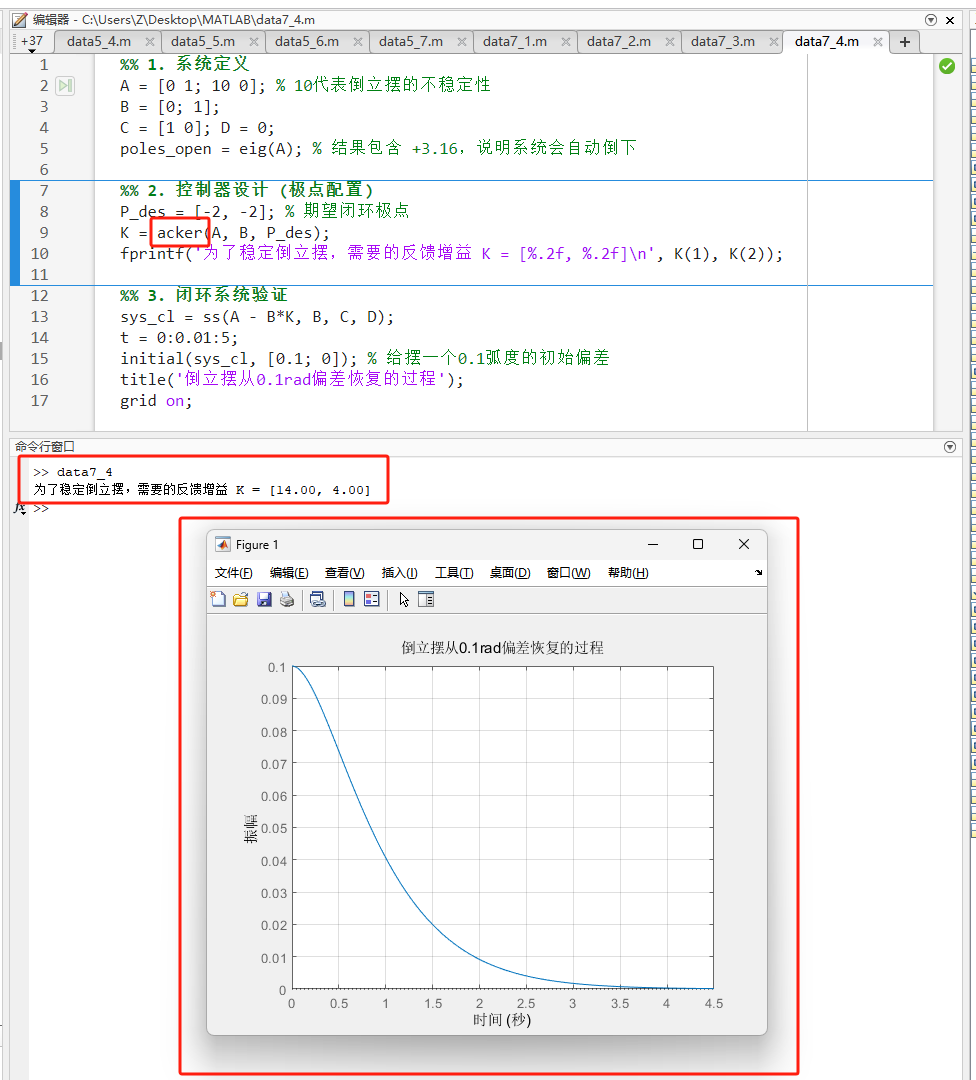
Simulink 搭建教程(详细):
-
新建模型 ,拖入
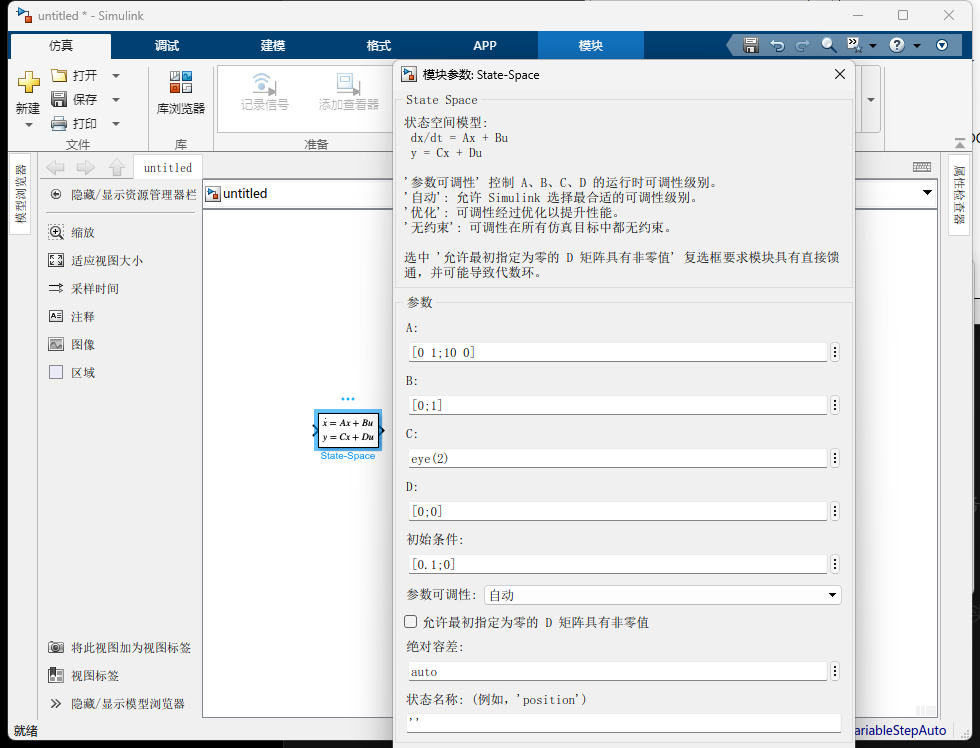
State-Space模块。 -
设置受控对象 :双击模块,A 填
[0 1; 10 0],B 填[0; 1],C 填eye(2)(为了输出所有状态),D 填[0; 0]。 -
设置初值 :在
Initial conditions填入[0.1; 0]。
-
加入反馈 :从输出连线,接一个
Gain模块。- 双击 Gain,值填入我们在 MATLAB 算的变量
K。 - 关键点 :
Multiplication选Matrix (K*u)。
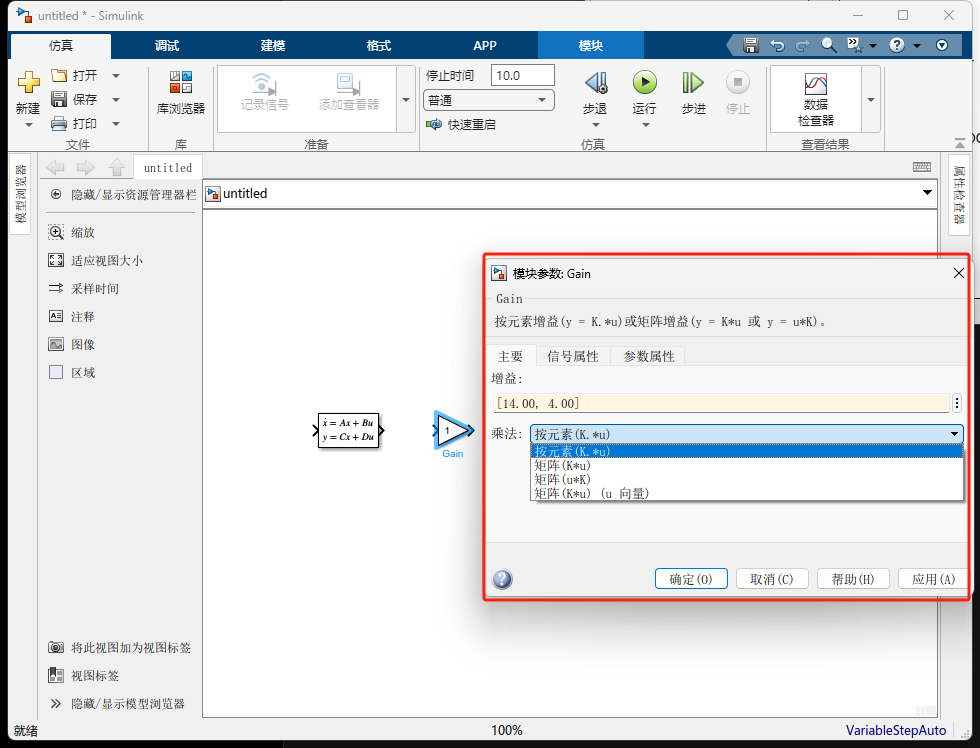
- 双击 Gain,值填入我们在 MATLAB 算的变量
-
负反馈 :将 Gain 的输出接回一个
Sum模块的-端。
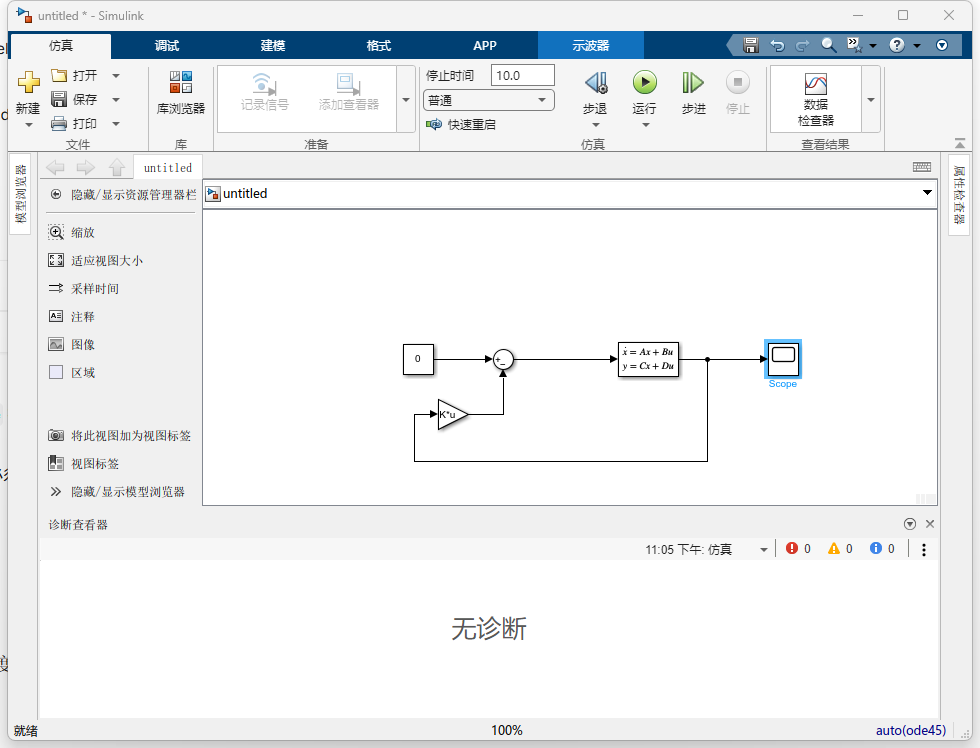
-
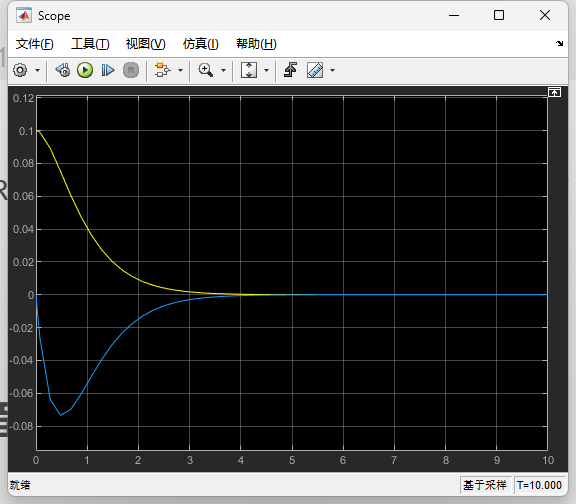
观察 :接上
Scope,点击 Run。你会看到状态曲线从 0.1 逐渐平滑回到了 0。
五、 第七章 语法与编程注意点
- 可控性检查 :在调用
place之前,必须先用rank(ctrb(A,B))检查。如果系统不可控,place会报错。 - LQR 的 Q 阵选择 :QQQ 必须是对称半正定矩阵。初学者常用
Q = C' * C或eye(n)。 - 分号的重要性:在处理大型矩阵设计时,结尾不加分号会导致屏幕被无用数据刷屏。
学习复习建议
- 重点攻克 :
sisotool。这是很多控制工程师在实际工作中使用率最高的工具。 - 思考题 :在倒立摆例子中,如果你把期望极点
P_des从[-2, -2]改为[-10, -10],控制电压(输入 uuu)会发生什么变化?- 提示:反应会极快,但所需的电机功率会巨大,甚至超过第六章讲的"饱和"限制。
经典设计方法就像是给系统做"微创手术"。如果你已经掌握了如何配置极点和最优控制,第八章我们将专门攻克工业界的"常青树"------PID 控制器。准备好开始第八章了吗?