第六章数据结构基础

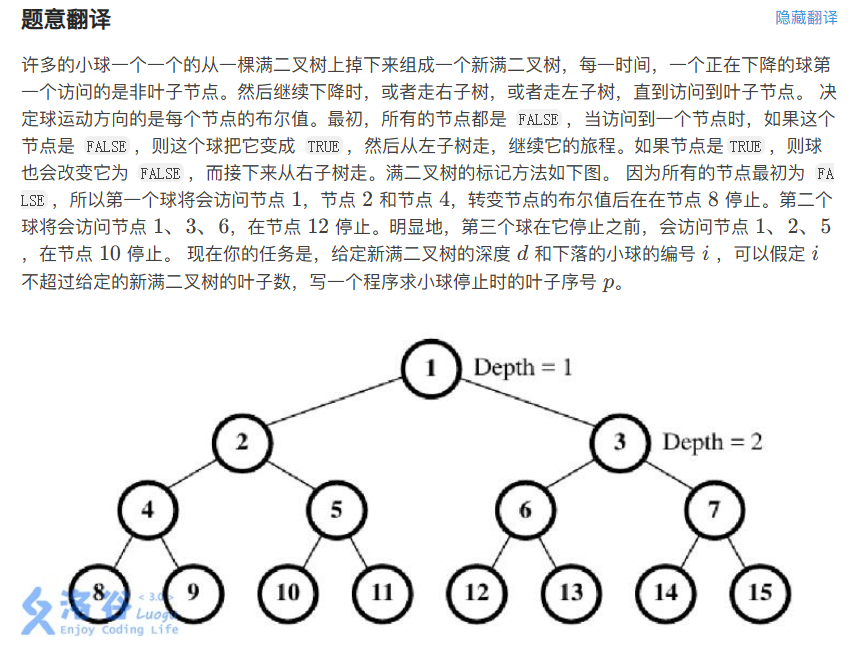
小球下落 Dropping Balls

每个节点有一个布尔开关 false 或 true，初始全为 false。
小球从根节点（节点 1）开始下落。
经过一个节点时：
- 若当前节点为 false → 小球把它变成 true，然后走向左子树。
- 若当前节点为 true → 小球把它变成 false，然后走向右子树。
小球一直下落到叶子节点时停止。

输入：

给多组测试数据，每组给 dd 和 ii（小球编号）。

输出：小球最终停下的叶子节点的编号。

思路：我们需要求第 I 个小球最终停在哪一个叶子节点。我发现根节点的选择完全由小球编号 I 决定：I 为奇数时 → 走左的是第(I+1)/2个小球；I 为偶数时 → 走右的是第I/2个小球。因此我用cur表示当前所在的节点编号，i 表示当前节点看到的小球"局部编号"（到达当前节点的第几个小球）。

用for循环从深度 1 迭代到深度 d − 1 中的每一层：

如果 i 是奇数：小球走左：cur = cur * 2，更新局部编号：i = (i+1)/2

如果 i 是偶数：小球走右：cur = cur * 2 + 1，更新局部编号：i = i/2

循环结束后返回叶子节点编号

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
int ball_stop(int d, int i) {
    int cur = 1;
    for (int k = 1; k < d; k++) {
        if (i % 2 == 1) {
            cur = cur * 2;
            i = (i + 1) / 2;
        } else {
            cur = cur * 2 + 1;
            i = i / 2;
        }
    }
    return cur;
}

int main() {
    int T;
    cin >> T;
    while(T--){
        int d, i;
        cin >> d;
        if(d==-1) break;
        cin >> i;
        cout << ball_stop(d, i) << endl;
    }
    return 0;
}

树的层次遍历 Trees on the level

Shuchong 给您一个二叉树，您的任务是写一个程序来输出依「阶层（level-order）」遍历的结果。在本问题中，二叉树的每个节点含有一个正整数，并且节点的数目在 [1,256] 的范围内。在「阶层」遍历中，依阶层从低到高，同阶层从左到右的次序来列印。

Shuchong：例如下面这个二叉树的阶层遍历结果就为: 5,4,8,11,13,4,7,2,1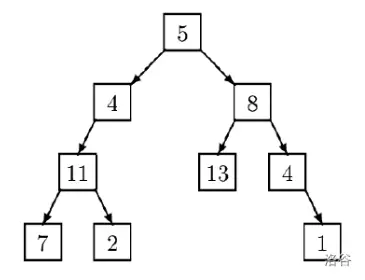

在本问题中，二叉树以节点来表示。每个节点以一个有序数对 (n,s) 来表示：

n 代表此节点的值
s 代表一个字符串，代表从根节点到达此节点的路径，其中 L 代表左，R 代表右

Shuchong：比如说上面那个值为 13 的节点用 (n,s) 的表示法就为 (13,RL)，值为 2 的节点用 (n,s) 的表示法就为 (2,LLR)，根节点 5 用 (n,s) 的表示法就为 (5,)。

看代码：

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
int main(){
	string s;
	while(cin >> s){
		if(s == "()") continue;
		
		vector<bool> has_value(1000,false);
		vector<int> value;
		map<int,int> nodes;//以图的方式存二叉树，nodes[1]为根 
		bool valid = true;
		
		
		do{//存储每组数据 
			if(s == "()") break;
			
			s = s.substr(1,s.length()-2);//去掉括号
			int comma = s.find(',');
			int val = stoi(s.substr(0,comma));//节点值 
			string path = s.substr(comma+1);//路径
			
			int pos = 1;//计算此节点在满二叉树中的位置 
			for(char c:path){
				if(c == 'L') pos = 2*pos;
				else if(c == 'R') pos = 2*pos+1;
			}
			if(has_value[pos]) valid = false;//已经存过值
			else {
				has_value[pos] = true;
				value.push_back(pos);
				nodes[pos] = val;//位置为pos的结点值为val 
			} 
		}while(cin >> s);
		
		if(!has_value[1]) valid = false;//没有根节点
		for(auto & p : nodes){//遍历树 
			int pos = p.first;
			if(pos > 1 && !has_value[pos/2]){
				valid = false;//父节点不存在 
				break;
			}
		} 
		if(!valid) cout << "not complete" << endl;
		else{//层次遍历 
			sort(value.begin(),value.end());//升序排序，确保按层输出
			for(size_t i=0;i<value.size();i++){
				if(i>0) cout << " ";
				cout << nodes[value[i]];
			}
			cout << endl;
		}
	} 
return 0;
}

Spreadsheet Calculator 电子表格计算器

使用 DFS 标记 in_stack 来检测环。检测是否存在环，如果存在环，标记所有环中的单元格。后递归计算依赖项

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

struct Cell {
    int val;
    string expr;
    bool is_num;
    bool visited, in_stack, in_cycle;
    vector<pair<int, int>> deps;
};

Cell sheet[20][20];
int n, m;

pair<int, int> parse(string s) {
    int c = 0, i = 0;
    while (isalpha(s[i])) {
        c = c * 26 + (s[i] - 'A' + 1);
        i++;
    }
    int r = stoi(s.substr(i));
    return {r, c - 1};
}

bool dfs(int r, int c, bool mark) {
    if (sheet[r][c].visited) return false;
    if (sheet[r][c].in_stack) {
        if (mark) sheet[r][c].in_cycle = true;
        return true;
    }
    
    sheet[r][c].in_stack = true;
    
    if (!sheet[r][c].is_num) {
        for (auto& d : sheet[r][c].deps) {
            if (dfs(d.first, d.second, mark)) {
                if (mark) sheet[r][c].in_cycle = true;
                sheet[r][c].in_stack = false;
                return true;
            }
        }
    }
    
    sheet[r][c].in_stack = false;
    sheet[r][c].visited = true;
    return false;
}

int calc(int r, int c) {
    if (sheet[r][c].is_num) return sheet[r][c].val;
    
    stringstream ss(sheet[r][c].expr);
    int res = 0, sign = 1;
    string token;
    
    while (ss >> token) {
        if (token == "+") sign = 1;
        else if (token == "-") sign = -1;
        else {
            int num;
            if (isalpha(token[0])) {
                auto p = parse(token);
                num = calc(p.first, p.second);
            } else {
                num = stoi(token);
            }
            res += sign * num;
        }
    }
    
    sheet[r][c].val = res;
    sheet[r][c].is_num = true;
    return res;
}

int main() {
    bool first = true;
    
    while (cin >> n >> m && n) {
        if (!first) cout << endl;
        first = false;
        
        // 读取
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                string s;
                cin >> s;
                
                sheet[i][j].expr = s;
                sheet[i][j].deps.clear();
                sheet[i][j].visited = sheet[i][j].in_stack = sheet[i][j].in_cycle = false;
                
                if (isdigit(s[0]) || (s[0] == '-' && isdigit(s[1]))) {
                    sheet[i][j].is_num = true;
                    sheet[i][j].val = stoi(s);
                } else {
                    sheet[i][j].is_num = false;
                    // 解析依赖
                    for (int k = 0; k < s.length(); k++) {
                        if (isalpha(s[k])) {
                            int start = k;
                            while (k < s.length() && (isalpha(s[k]) || isdigit(s[k]))) k++;
                            auto p = parse(s.substr(start, k - start));
                            sheet[i][j].deps.push_back(p);
                            k--;
                        }
                    }
                }
            }
        }
        
        // 检测环
        bool cycle = false;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (!sheet[i][j].visited) {
                    if (dfs(i, j, false)) cycle = true;
                }
            }
        }
        
        if (cycle) {
            // 重置并标记环中节点
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    sheet[i][j].visited = sheet[i][j].in_stack = sheet[i][j].in_cycle = false;
                }
            }
            
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    if (!sheet[i][j].visited) {
                        dfs(i, j, true);
                    }
                }
            }
            
            // 输出环中单元格
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    if (sheet[i][j].in_cycle) {
                        cout << char('A' + j) << i << ": " << sheet[i][j].expr << endl;
                    }
                }
            }
        } else {
            // 计算并输出
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    if (!sheet[i][j].is_num) {
                        calc(i, j);
                    }
                }
            }
            
            // 输出表格
            cout << "     ";
            for (int j = 0; j < m; j++) cout << "    " << j;
            cout << endl;
            
            for (int i = 0; i < n; i++) {
                printf("%5d:", i);
                for (int j = 0; j < m; j++) {
                    printf("%5d", sheet[i][j].val);
                }
                cout << endl;
            }
        }
    }
    
    return 0;
}

第六章 数据结构基础

第六章数据结构基础