
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 逆序对](#1. 逆序对)
[2. 求第 k 小的数](#2. 求第 k 小的数)
[3. 最大子段和](#3. 最大子段和)
[4. 地毯填补问题](#4. 地毯填补问题)
前言
分治全称为分而治之。指把一个大问题转化为几个小的子问题,把所有的子问题解决完了,自然解决了整个大问题
1. 逆序对
题目链接:

算法原理
分治是解决[逆序对]问题最经典的做法
我们把原数组从中间mid一分为二
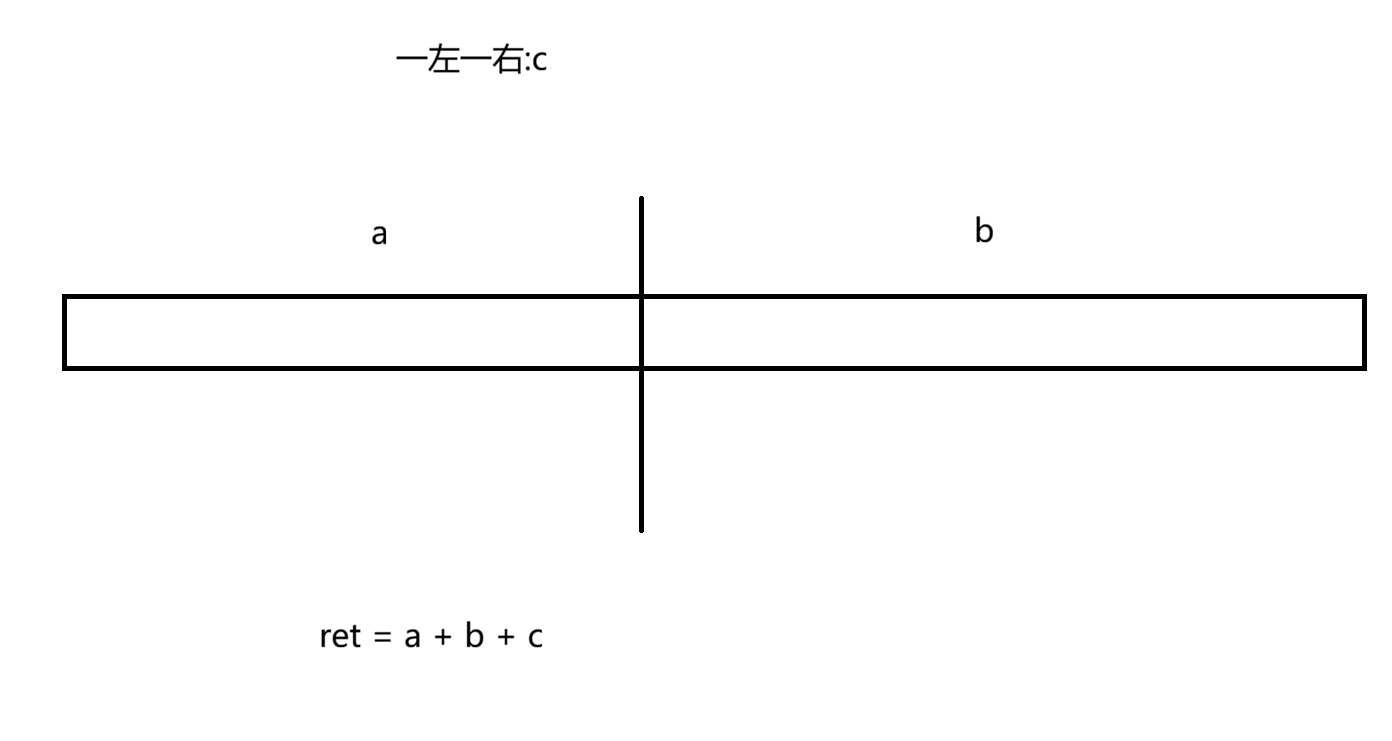
那么答案包含以下三种
- 左边数组总逆序对个数a
- 右边数组总逆序对个数b
- 左数组选一个数,右数组选一个数,构成逆序对的总个数c
那么总个数ret = a + b + c
同理,我们继续划分,把左数组再一分为二讨论,右数组一分为二讨论,然后再划分......
直到数组无法划分(只有一个数)
当左数组答案和右数组答案得到时,要处理的是一左一右的情况,这个时候我们可以排序
例如排完序得到:
1 5 6 / 2 4 8
那么我可以利用双指针求解:
定义cur1从左往右遍历左数组,定义cur2从左往右遍历右数组,cnt为构成逆序对的个数
当v[cur1] > v[cur2]时,cur2++,cnt += (mid - cur1 + 1) ,因为当v[cur1] > v[cur2]时,也表明cur1之后的所有元素都大于v[cur2](因为单调递增)
当v[cur1] <= v[cur2]时,cur1++
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> v;
long long merge(int left,int right)
{
if(left >= right)
return 0;
int mid = (left + right)/2;
long long ret = 0;
ret += merge(left,mid);
ret += merge(mid+1,right);
sort(v.begin() +left,v.begin() +mid + 1);
sort(v.begin() +mid + 1,v.begin() + right + 1);
int cur1 = left;
int cur2 = mid + 1;
while(cur1 <= mid && cur2 <=right)
{
if(v[cur1] <= v[cur2])
cur1++;
else
{
ret += mid - cur1 + 1;
cur2++;
}
}
return ret;
}
int main()
{
int n;cin>>n;
for(int i = 0;i<n;i++)
{
int num;cin>>num;
v.push_back(num);
}
cout<<merge(0,v.size()-1);
return 0;
}2. 求第 k 小的数
题目链接:
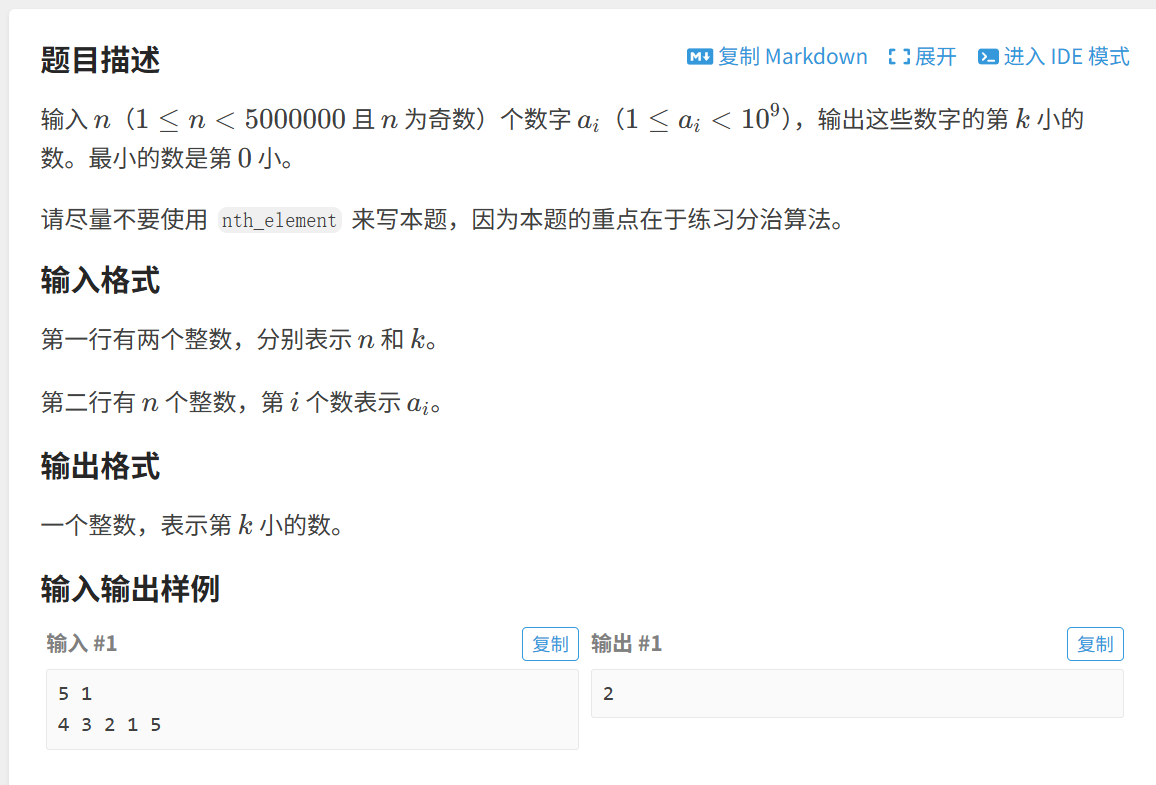
算法原理
我们使用快排的思想,进行三路划分
- 定义区间[left,right],key为数组下标为left的元素的值
- begin初始化为left,end初始为right,cur从begin + 1开始遍历
- 当v[cur] < key,交换v[cur]和v[begin]的值,同时cur++,left++
- 当v[cur] > key,交换v[cur]和v[end]的值,同时end--
- 当v[cur] == key时,cur++
- 当cur > right时,循环停止
这样保证一趟循环后,数组分为三个区间
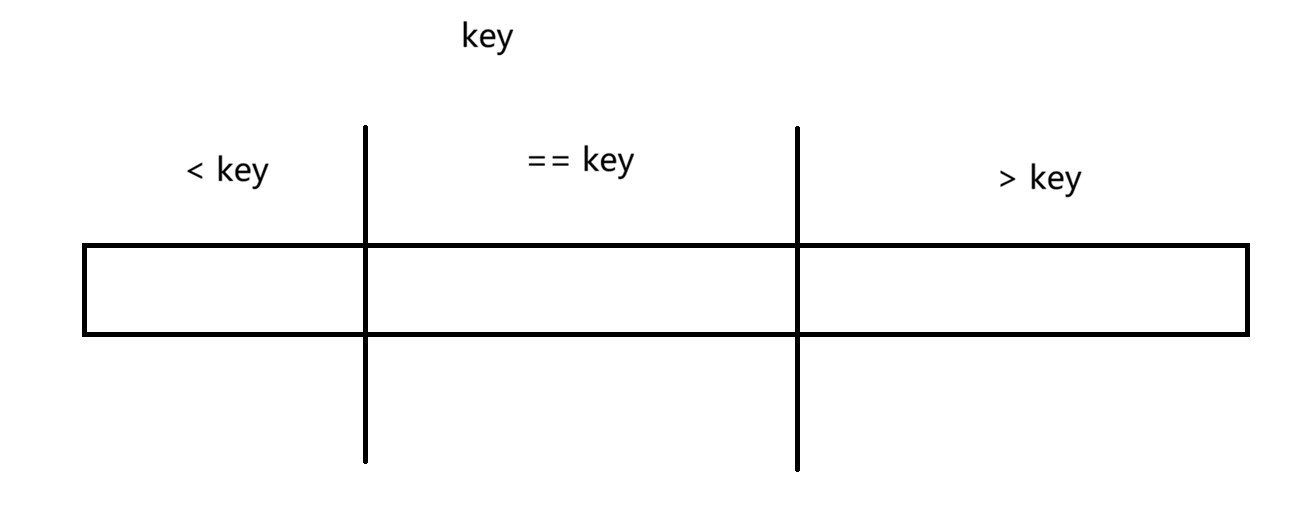
即左区间全为小于key 的值,中间区间全为等于key 的值,右区间全为大于key的值
这样我们再看找第k小的值,就很好找了
假设左区间的个数为c1,中间区间的个数为c2
- 如果k <= c1,那么整个数组第k小的数,一定在左边的区间
- 如果c1 < k <= c1 + c2,那么k落在中间的区间,则第k小的数一定为key
- 如果c1 + c2 < k,那么第k小的数一定在右边的区间,这个时候在右区间找第k - c1 - c2小的数即可
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
vector<long long> v;
long long merge(int left, int right, int k)
{
int begin = left;int cur = begin + 1;
int end = right;long long key = v[left];
while(cur <= end)
{
if(v[cur] > key)
{
swap(v[cur],v[end]);
end--;
}
else if(v[cur] < key)
{
swap(v[cur],v[begin]);
begin++;
cur++;
}
else
cur++;
}
int c1 = begin - left;int c2 = end - begin + 1;
if(k <= c1)
return merge(left,begin - 1,k);
else if(k <= c1 + c2)
return key;
else
return merge(end + 1,right,k - c1 - c2);
}
int main()
{
int n, k;
cin >> n >> k;
k++;
v.resize(n);
for (int i = 0; i < n; i++)
scanf("%lld", &v[i]);
cout << merge(0, n - 1, k) << endl;
return 0;
}3. 最大子段和
题目链接:

算法原理
如果把整个序列[l,r]从中间mid位置分成两部分,那么整个序列中所有的子数组就分成三部分:
- 子数组在区间[l,mid]内;
- 子数组在区间[mid+1,r]内;
- 子数组的左端点在[l,mid]内,右端点在[mid+1,r]内。
那么我们的「最终结果」也会在这三部分取到,要么在左边区间,要么在右边区间,要么在跨越中轴线的区间。因此,我们可以先求出左边区间的最大子段和,再求出右边区间的最大子段和,最后求出中间区间的最大子段和。其中求「左右区间」时,可以交给「递归」去解决。
那我们重点处理如何求出「中间区间」的最大子段和。可以把中间区间分成两部分
- 左边部分是从mid为起点,「向左延伸」的最大子段和
- 右边部分是从mid+1为起点,「向右延伸」的最大子段和
分别求出这两个值,然后相加即可。
实操代码
cpp
#include <iostream>
using namespace std;
const int N = 2e5 + 10;
int n;
int a[N];
int dfs(int l, int r)
{
if(l == r) return a[l];
int mid = (l + r) >> 1;
// 先求⼀下左右两边的最⼤值
int ret = max(dfs(l, mid), dfs(mid + 1, r));
int suml = a[mid], sumr = a[mid + 1];
int maxl = suml, maxr = sumr;
// 求出以 a[mid] 开始,向左延伸的最⼤值
for(int i = mid - 1; i >= l; i--)
{
suml += a[i];
maxl = max(maxl, suml);
}
// 求出以 a[mid + 1] 开始,向右延伸的最⼤值
for(int i = mid + 2; i <= r; i++)
{
sumr += a[i];
maxr = max(maxr, sumr);
}
// 返回三种情况的最⼤值
return max(maxr + maxl, ret);
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
cout << dfs(1, n) << endl;
return 0;
}4. 地毯填补问题
题目链接:

算法原理
一维分治的时候我们是从把区间从中间切开,那二维分治我们如何处理?
我们把整个二维矩阵从中间切两刀,分成四个相等的小矩阵
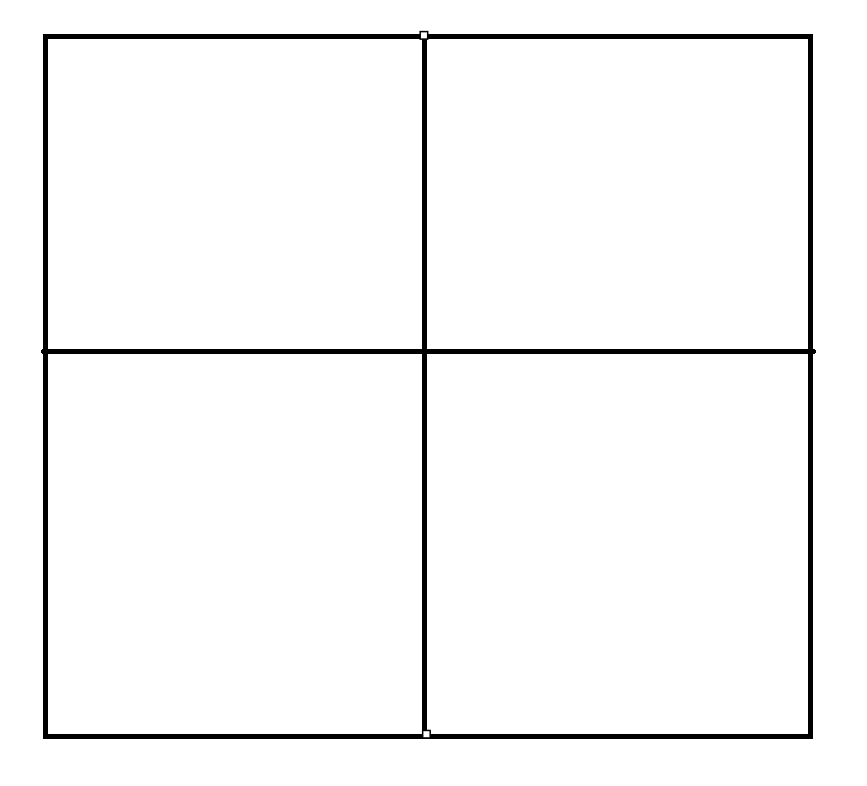
由于公主在某个格子内,我们假设在左上角的矩阵内
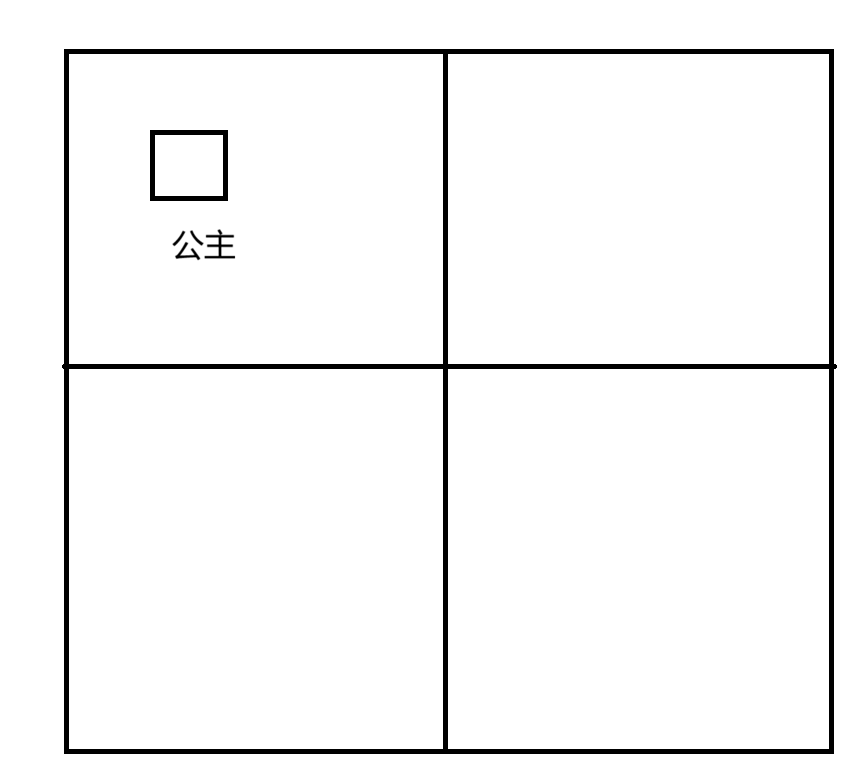
我们处理分治的核心是:处理几个相同的子问题
而现在显然子问题不相同,因为只有一个小矩阵有公主
那么既然其他三个矩阵没公主,我们就分别创造一个假公主给其余的三个矩阵
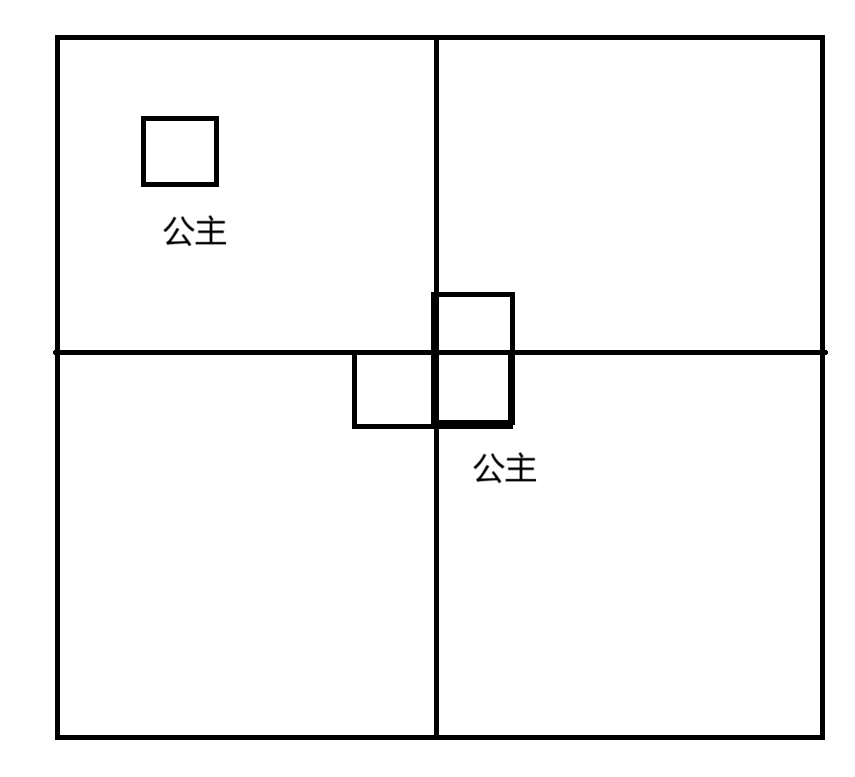
根据地毯的形状,我们可以在中心处这样铺,这样其余的三个矩阵就都多出了一个额外的方块,然后我们假设这个方块是公主,就可以对4个矩阵继续分治了
当然公主也有可能不在左上角,但无论在哪,我们都有对应的铺法
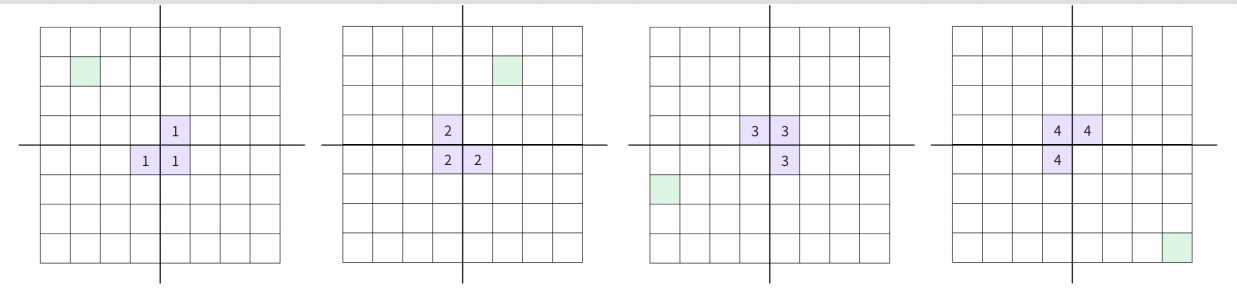
一直分治直到矩阵只有1个方格即可
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
void dfs(int a, int b, int len, int x, int y)
{
if (len == 1)
return;
len /= 2;
if (x < a + len && y < b + len)
{
cout << a + len << " " << b + len << " "<<"1" << endl;
dfs(a, b, len, x, y);
dfs(a, b + len, len, a + len - 1, b + len);
dfs(a + len, b, len, a + len, b + len - 1);
dfs(a + len, b + len, len, a + len, b + len);
}
else if (x < a + len && y >= b + len)
{
cout << a + len << " " << b + len - 1 << " " << "2" << endl;
dfs(a, b, len, a + len - 1, b + len - 1);
dfs(a, b + len, len, x, y);
dfs(a + len, b, len, a + len, b + len - 1);
dfs(a + len, b + len, len, a + len, b + len);
}
else if (x >= a + len && y < b + len)
{
cout << a + len - 1 << " " << b + len << " " << "3" << endl;
dfs(a, b, len, a + len - 1, b + len - 1);
dfs(a, b + len, len, a + len - 1, b + len);
dfs(a + len, b, len, x, y);
dfs(a + len, b + len, len, a + len, b + len);
}
else
{
cout << a + len - 1 << " " << b + len - 1 << " " << "4" << endl;
dfs(a, b, len, a + len - 1, b + len - 1);
dfs(a, b + len, len, a + len - 1, b + len);
dfs(a + len, b, len, a + len, b + len - 1);
dfs(a + len, b + len, len, x, y);
}
}
int main()
{
int k, x, y; cin >> k>>x >> y;
int len = (1 << k);
dfs(1, 1, len, x, y);
return 0;
}