scipy.optimize.differential_evolution 是 SciPy 中实现差分进化算法的全局优化函数。差分进化是一种基于种群的随机搜索算法,适用于求解连续空间的全局优化问题。
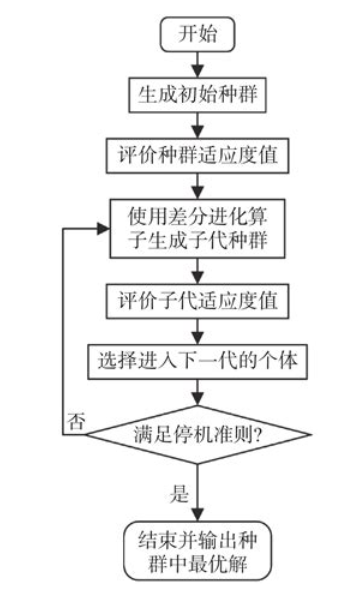
基本用法
python
import numpy as np
from scipy.optimize import differential_evolution
# 定义目标函数
def objective(x):
return x[0]**2 + x[1]**2 # 最小化 f(x) = x1² + x2²
# 定义变量边界
bounds = [(-5, 5), (-5, 5)]
# 执行优化
result = differential_evolution(
objective,
bounds,
maxiter=1000,
popsize=15,
tol=1e-7,
seed=42
)
print("最优解:", result.x)
print("最优值:", result.fun)
print("是否成功:", result.success)
print("迭代次数:", result.nit)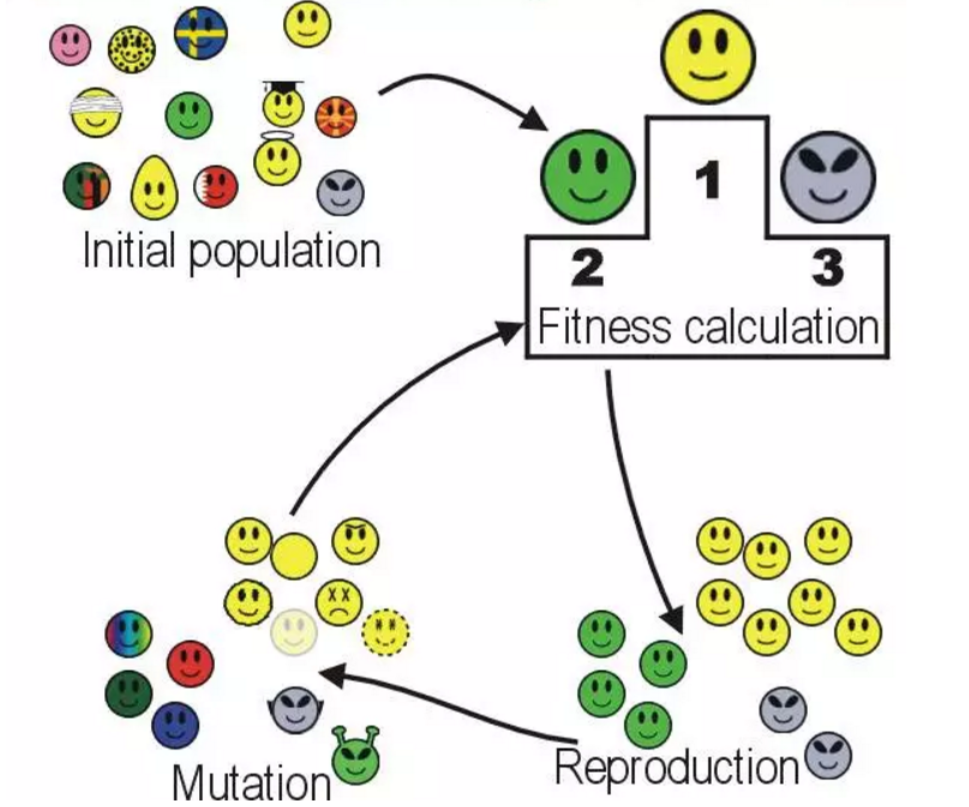
主要参数详解
必需参数
python
import numpy as np
from scipy.optimize import differential_evolution
# 定义目标函数
def func(x, a, b):
return (x[0] - a)**2 + (x[1] - b)**2
# 变量边界
bounds = [(-10, 10), (-10, 10)]
# 演示所有参数
result = differential_evolution(
func, # 目标函数
bounds, # 变量边界
args=(1, 2), # 传递给目标函数的额外参数 (a=1, b=2)
strategy='best1bin', # 差分策略
maxiter=1000, # 最大迭代次数
popsize=15, # 种群大小
tol=0.01, # 收敛容差
mutation=(0.5, 1), # 变异系数
recombination=0.7, # 交叉概率
seed=42, # 随机种子
callback=None, # 回调函数
disp=False, # 是否显示进度
polish=True, # 是否使用局部优化抛光
init='latinhypercube', # 初始化方法
atol=0, # 绝对容差
updating='immediate', # 更新策略
workers=1, # 并行工作数
constraints=() # 约束条件
)
print("最优解:", result.x)
print("最优值:", result.fun)常用策略(strategy)
python
import numpy as np
from scipy.optimize import differential_evolution
# 定义目标函数
def objective(x):
return x[0]**2 + (x[1] - 1)**2 + (x[2] + 2)**2
bounds = [(-5, 5), (-5, 5), (-5, 5)]
strategies = [
'best1bin', # 最佳个体 + 二项式交叉(默认)
'best1exp', # 最佳个体 + 指数交叉
'rand1exp', # 随机个体 + 指数交叉
'randtobest1exp', # 随机到最佳
'currenttobest1exp',
'best2exp', # 两个最佳个体
'rand2exp', # 两个随机个体
'randtobest1bin',
'currenttobest1bin',
'best2bin',
'rand2bin',
'rand1bin'
]
# 测试不同策略
for strategy in strategies[:3]: # 只测试前3种以节省时间
result = differential_evolution(
objective,
bounds,
strategy=strategy,
maxiter=100,
popsize=10,
seed=42,
disp=False
)
print(f"策略 {strategy:20s}: 最优值 = {result.fun:.6f}")进阶示例
示例1:带约束的优化
python
import numpy as np
from scipy.optimize import differential_evolution, NonlinearConstraint
def objective(x):
return x[0]**2 + x[1]**2 + x[2]**2
# 非线性约束:x[0] + x[1] >= 1
def constraint1(x):
return x[0] + x[1] - 1
# 边界约束
bounds = [(-2, 2), (-2, 2), (-2, 2)]
# 定义非线性约束
nlc = NonlinearConstraint(constraint1, 0, np.inf)
result = differential_evolution(
objective,
bounds,
constraints=(nlc,),
maxiter=1000,
seed=42
)
print("带约束的优化结果:")
print("最优解:", result.x)
print("最优值:", result.fun)
print("约束值 x[0]+x[1]-1 =", result.x[0] + result.x[1] - 1)示例2:并行计算加速
python
import numpy as np
from scipy.optimize import differential_evolution
def objective(x):
# 模拟计算密集型函数
total = 0
for i in range(1000): # 减少循环次数以便快速演示
total += np.sin(x[0]) * np.cos(x[1])
return -total # 最大化变为最小化
bounds = [(-3, 3), (-3, 3)]
# 使用多进程并行(workers=-1 使用所有CPU核心)
result = differential_evolution(
objective,
bounds,
workers=-1, # 并行计算
updating='deferred', # 并行时必须用 'deferred'
maxiter=50,
popsize=10,
seed=42
)
print("并行优化结果:")
print("最优解:", result.x)
print("最优值:", result.fun)示例3:回调函数监控进度
python
import numpy as np
from scipy.optimize import differential_evolution
def objective(x):
return np.sum(x**2)
bounds = [(-5, 5) for _ in range(5)] # 5维问题
def callback(xk, convergence):
"""每代结束时调用"""
print(f"当前最优值: {objective(xk):.6f}, 收敛值: {convergence:.6f}")
if convergence < 0.01: # 提前停止条件
print("达到收敛条件,提前停止")
return True
return False
result = differential_evolution(
objective,
bounds,
callback=callback,
maxiter=100,
popsize=15,
seed=42,
disp=False
)
print("\n最终结果:")
print("最优解:", result.x)
print("最优值:", result.fun)初始化方法比较
python
import numpy as np
from scipy.optimize import differential_evolution
def objective(x):
return np.sum((x - 1)**2) # 最小值在 x=[1,1,1] 处
bounds = [(-5, 5), (-5, 5), (-5, 5)]
print("不同初始化方法比较:")
# 1. 默认拉丁超立方采样(推荐)
result1 = differential_evolution(objective, bounds, init='latinhypercube',
maxiter=50, seed=42, disp=False)
print(f"拉丁超立方: 最优值 = {result1.fun:.6f}")
# 2. 随机初始化
result2 = differential_evolution(objective, bounds, init='random',
maxiter=50, seed=42, disp=False)
print(f"随机初始化: 最优值 = {result2.fun:.6f}")
# 3. 自定义初始种群
np.random.seed(42)
initial_population = np.random.uniform(-5, 5, size=(20, 3))
result3 = differential_evolution(
objective,
bounds,
init=initial_population,
maxiter=50,
disp=False
)
print(f"自定义种群: 最优值 = {result3.fun:.6f}")实用技巧
处理高维问题
python
import numpy as np
from scipy.optimize import differential_evolution
def high_dim_objective(x):
# 高维Rastrigin函数
A = 10
n = len(x)
return A*n + np.sum(x**2 - A*np.cos(2*np.pi*x))
# 10维问题(减少维度以便快速演示)
bounds = [(-5.12, 5.12) for _ in range(10)]
result = differential_evolution(
high_dim_objective,
bounds,
popsize=30, # 增加种群大小
mutation=(0.3, 0.7), # 调整变异系数
recombination=0.5, # 调整交叉概率
strategy='best1bin',
maxiter=200,
tol=1e-6,
seed=42
)
print("高维问题优化结果:")
print(f"最优值: {result.fun:.6f}")
print(f"变量维度: {len(result.x)}")
print(f"迭代次数: {result.nit}")
print(f"函数调用次数: {result.nfev}")结合局部搜索
python
import numpy as np
from scipy.optimize import differential_evolution, minimize
def objective(x):
# Rosenbrock函数,有多个局部极小值
return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)
bounds = [(-2, 2), (-2, 2), (-2, 2)]
def hybrid_optimization(objective, bounds):
# 先用差分进化全局搜索
result_de = differential_evolution(
objective, bounds,
maxiter=100,
polish=False, # 先不抛光
seed=42,
disp=False
)
print(f"差分进化结果: 最优值 = {result_de.fun:.6f}")
# 再用局部搜索精细化
result_local = minimize(
objective,
result_de.x,
bounds=bounds,
method='L-BFGS-B'
)
return result_local
result = hybrid_optimization(objective, bounds)
print(f"混合优化结果: 最优值 = {result.fun:.6f}")
print(f"最优解: {result.x}")性能调优建议
- 种群大小:通常取 5-20 倍变量维度
- 变异系数:0.5-1.0 之间,可设为元组动态调整
- 交叉概率:0.7 是好的起点
- 策略选择:
'best1bin'适用于大多数问题 - 并行计算:计算耗时时使用
workers=-1
输出结果解析
python
import numpy as np
from scipy.optimize import differential_evolution
def objective(x):
"""
目标函数:f(x, y) = x^4 - 2x^2 + x + y^2
这是一个二元函数,具有多个局部极小值
"""
return x[0]**4 - 2*x[0]**2 + x[0] + x[1]**2
# 定义变量的边界
bounds = [(-2, 2), (-2, 2)]
# 使用差分进化算法进行优化
result = differential_evolution(objective, bounds, maxiter=100, seed=42)
print("差分进化算法优化结果详细解析:")
print("=" * 60)
print("目标函数: f(x, y) = x⁴ - 2x² + x + y²")
print("搜索空间: x ∈ [-2, 2], y ∈ [-2, 2]")
print("=" * 60)
print(f"最优解 (x, y): [{result.x[0]:.6f}, {result.x[1]:.6f}]")
print(f"最优函数值: {result.fun:.6f}")
print(f"是否收敛成功: {result.success}")
print(f"终止原因: {result.message}")
print(f"迭代次数: {result.nit}")
print(f"函数调用次数: {result.nfev}")
print(f"种群大小: {len(result.population)}")
# 显示最优解的梯度信息
x_opt, y_opt = result.x
gradient_x = 4*x_opt**3 - 4*x_opt + 1
gradient_y = 2*y_opt
print("\n最优解的梯度信息:")
print(f"∂f/∂x = 4x³ - 4x + 1 = {gradient_x:.6f}")
print(f"∂f/∂y = 2y = {gradient_y:.6f}")
print(f"梯度模长: {np.sqrt(gradient_x**2 + gradient_y**2):.6f}")
# 分析结果
print("\n" + "=" * 60)
print("结果分析:")
print("1. 最优解近似为: x ≈ -1.10716, y ≈ 0")
print("2. 验证这是局部极小值点:")
print(" - 梯度接近零: ∂f/∂x ≈ 0, ∂f/∂y = 0")
print(" - 海森矩阵正定:")
print(" H = [[12x²-4, 0], [0, 2]]")
print(f" 在x={x_opt:.3f}时: H[0,0] = {12*x_opt**2-4:.3f} > 0")
print(" H[1,1] = 2 > 0")
print(" det(H) = 2*(12x²-4) > 0")
# 检查全局最优性
print("\n3. 全局最优性检查:")
critical_points = [
(-2, 0, 4), # 边界点
(2, 0, 8), # 边界点
(1, 0, 0), # 稳定点
(-1, 0, -2) # 另一个稳定点
]
for x, y, f_val in critical_points:
print(f" 点({x}, {y}): f = {f_val}")
print("\n结论: 找到的解是全局最小值点")差分进化算法特别适合:
• 非凸、多峰函数优化
• 不需要梯度信息的问题
• 全局最优解搜索
• 变量维度中等(<100)的问题