【经典论文精读（一）】Isomap：非线性降维的全局几何框架（Science 2000）

deep_drink2026-01-24 13:54

Tenenbaum, J. B., De Silva, V., & Langford, J. C. (2000). A global geometric framework for nonlinear dimensionality reduction. Science, 290(5500), 2319-2323.

今天我们要"考古"一篇发表于 2000 年 Science 杂志 的神级论文------Isomap。

流形学习的鼻祖：它教会我们如何像"蚂蚁"一样在曲面上感知距离，而不是像"苍蝇"一样飞越欧氏空间。这种测地线 (Geodesic) 的思想，是处理点云非刚性形变（Non-rigid Deformation）的基石。

数学的美感：不同于现在神经网络的黑盒，Isomap 的推导（从 Floyd 最短路到 MDS 特征分解）逻辑严密，每一步都有完美的数学解释。

硬核干货：本文不仅讲解 Isomap 算法流程，还特别手推了论文中针对手写数字识别使用的"切空间距离 (Tangent Distance)"------这是一个常被忽略，但能有效解决旋转/缩放不变性的数学利器。

如果你厌倦了调参，想静下心来从数学底层理解"数据流形"，那么这篇文章就是为你准备的。让我们一起拆解这篇 Science 经典，看看非线性降维的全局几何框架究竟长什么样。

1. 论文的核心观点：数据是高维的，但本质是低维的

为什么这么说？

科学家经常面临处理大量高维数据的挑战，例如全球气候模式、人类基因分布或图像视频。以一张 64 × 64 64 \times 64 64×64 像素的人脸图像为例，它在数学上是一个 4096 维的向量（ 64 2 = 4096 64^2=4096 642=4096）。然而，控制这一张人脸图像变化的物理变量（自由度）其实非常少，比如：上下转头、左右转头、光照方向。

这意味着，虽然数据"居住"在一个 4096 维的观察空间里，但它们实际上只是分布在一个卷曲的、低维的（例如 3 维）流形（Manifold）上。

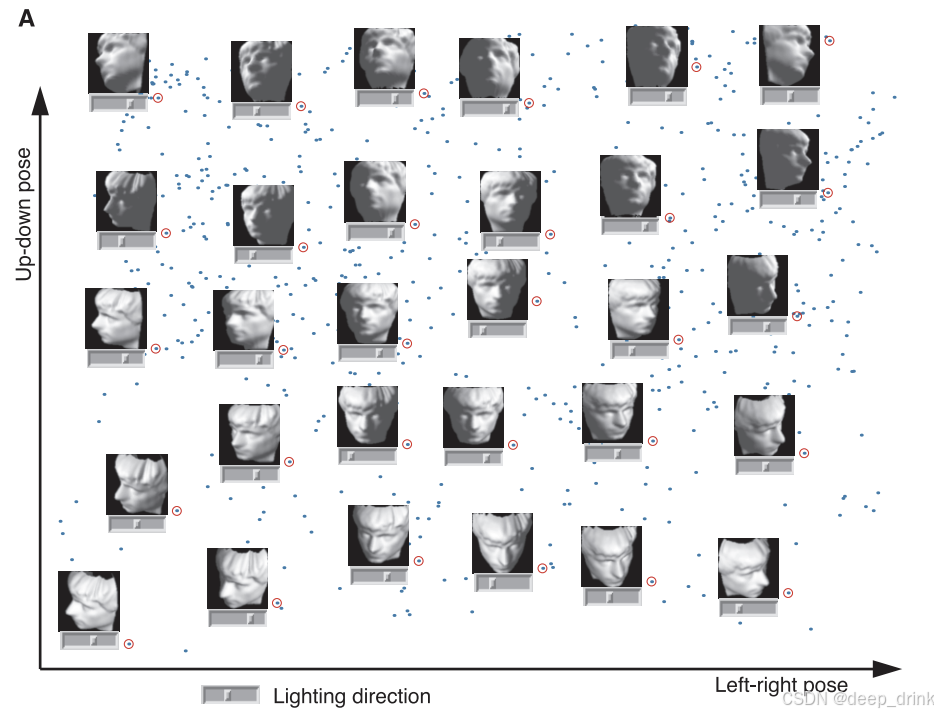
  • 图 1 (A) 人脸数据嵌入 ：

    Isomap 将 698 张高维人脸图像映射到了 3 维空间。结果显示，这三个坐标轴自动对应了图像的内在自由度：

    • X 轴：左右姿态（Left-right pose）
    • Y 轴：上下姿态（Up-down pose）
    • 滑块轴 ：光照方向（Lighting direction）
      这证明算法在没有任何监督的情况下，发现了数据的物理生成机制。

  • 图 1 (B) 手写数字 '2' 的嵌入 ：

    Isomap 将 1000 个手写数字 "2" 映射到了二维空间。结果显示，这两个坐标轴自动对应了手写风格的内在自由度：

    • X 轴：底部圆环的形状（Bottom loop articulation），从左侧带有明显大圆环的写法，过渡到右侧底部为直线的写法。
    • Y 轴 ：顶部拱形的形状（Top arch articulation），从下侧尖锐的"V"形弯钩，过渡到上侧圆润的拱形弯钩。
      图中伸出的"触须"（Tendrils）代表了某些极端的、带有额外装饰笔画的罕见写法。

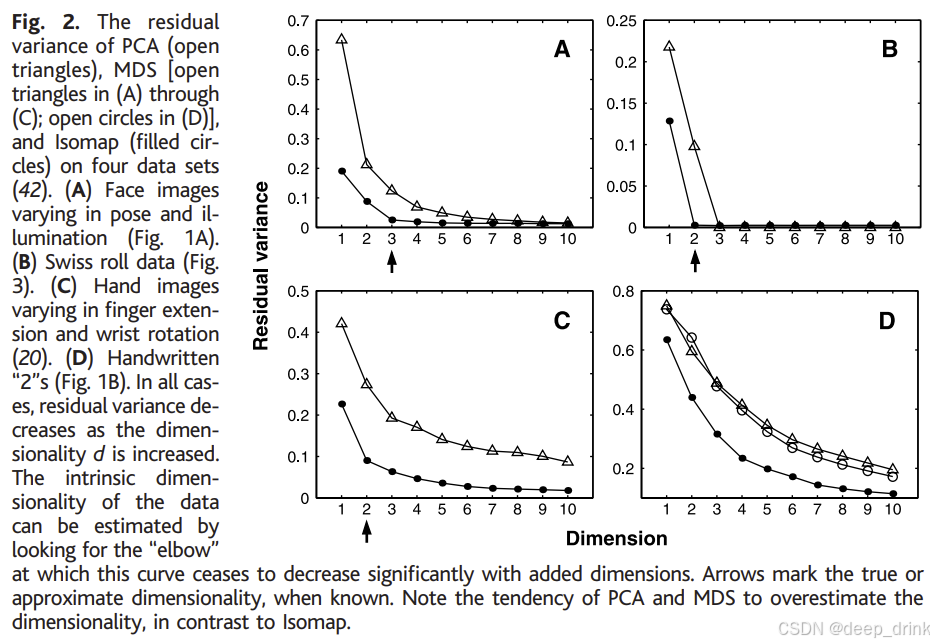
  • 图 2 残差方差（The Elbow Curve） ：

    这是评估降维效果的关键图表。横轴是维度 d d d，纵轴是残差方差（越低越好）。

    • 现象 ：Isomap（实心点）的误差曲线在达到真实维度（如瑞士卷 d = 2 d=2 d=2，人脸 d = 3 d=3 d=3）时急剧下降，形成一个明显的"肘部"（Elbow）。
    • 对比：传统线性方法 PCA 和 MDS（空心点）无法发现这种非线性结构，往往高估数据的维度，误差下降缓慢。

2. 论文要干什么：构建全局测地线距离

核心目标：把卷曲的流形"铺平"。

传统方法（PCA/MDS）使用的是欧氏距离（Euclidean distance），这相当于在空间中走直线（穿墙术）。对于卷曲的"瑞士卷"结构，这会错误地将流形上相距很远的点（比如卷的两层）判为邻居。

Isomap 的目标是计算流形上的测地线距离（Geodesic distance），即沿着曲面爬行的距离。只有保持了这个距离，才能真正恢复数据的低维几何结构。

3. 论文怎么去做的：Isomap 三部曲

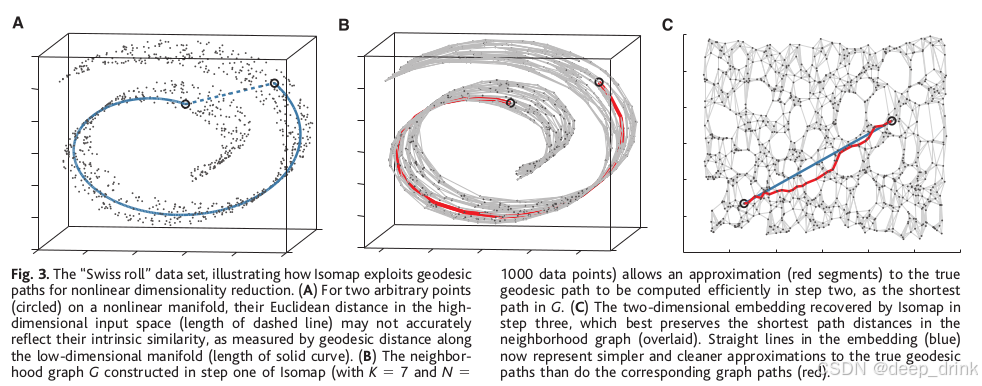
Isomap 的算法流程极其简洁，主要分为三步。结合图 3（瑞士卷展开过程）进行讲解：

Step 1: 构建邻域图 (Construct Neighborhood Graph)

我们需要定义局部的连通性（对应图 3B）。

  • 计算所有点对 ( i , j ) (i, j) (i,j) 之间的输入空间距离 d X ( i , j ) d_X(i,j) dX(i,j)。
  • 建图规则 ：
    • K K K-Isomap ：连接最近的 K K K 个邻居。
    • ϵ \epsilon ϵ-Isomap ：连接所有距离小于 ϵ \epsilon ϵ 的点。
  • 边权重设为 d X ( i , j ) d_X(i,j) dX(i,j)。
  • 特别注意 ：对于手写数字数据集，论文使用了切空间距离 (Tangent Distance) 来代替欧氏距离，以消除旋转和变形的影响。

Step 2: 计算最短路径 (Compute Shortest Paths)

这是算法的灵魂。通过局部距离的传递，近似全局测地线距离（对应图 3B 中的红线）。
算法 ：使用 Floyd-Warshall 算法 更新距离矩阵 D G D_G DG：

d G ( i , j ) = min ⁡ { d G ( i , j ) , d G ( i , k ) + d G ( k , j ) } d_G(i,j) = \min \{ d_G(i,j), \quad d_G(i,k) + d_G(k,j) \} dG(i,j)=min{dG(i,j),dG(i,k)+dG(k,j)}

这一步将稀疏的邻接矩阵转化为稠密的全局测地线距离矩阵，其中 D G ( i , j ) D_G(i,j) DG(i,j) 近似于流形上的真实距离 d M ( i , j ) d_M(i,j) dM(i,j)。

Step 2: 计算最短路径 (Compute Shortest Paths)

这一步是 Isomap 的"灵魂"。在 Step 1 中，我们只知道谁和谁是邻居（局部距离）；在 Step 2 中，我们要计算任意两点之间的距离。

1. 核心思想：以"图"代"面"

我们假设数据所在的流形是光滑的。对于流形上相距很远的两个点 A 和 B：

  • 直线距离（欧氏距离）：是错误的，因为它穿过了流形弯曲的空间（像"穿墙术"）。
  • 测地线距离：是正确的，它是沿着流形表面走的距离。

Isomap 的策略 ：利用邻域图（Neighborhood Graph）。如果邻居选得足够密，那么图上的最短路径（Shortest Path on Graph） 就会极其逼近流形上的 测地线距离（Geodesic Distance）。

2. 具体的算法：Floyd-Warshall

原论文采用了 Floyd-Warshall 算法 来计算图中所有节点对之间的最短路径。这是一个基于动态规划（Dynamic Programming）的算法。

解释：要求所有的点之间的距离。先随机一个点，然后看其他经过该点的路径是不是缩短了。

算法流程：

  • 初始化距离矩阵 D G D_G DG ( N × N N \times N N×N)：

    • 如果点 i i i 和点 j j j 是邻居（在 Step 1 中连了边），则 D G ( i , j ) = d X ( i , j ) D_G(i,j) = d_X(i,j) DG(i,j)=dX(i,j)（也就是它俩的欧氏距离或切空间距离）。
    • 如果点 i i i 和点 j j j 不是邻居，则 D G ( i , j ) = ∞ D_G(i,j) = \infty DG(i,j)=∞（无穷大）。
    • 对角线元素 D G ( i , i ) = 0 D_G(i,i) = 0 DG(i,i)=0。

  • 迭代更新 (The Core Loop) ：

    我们需要遍历每一个点 k k k ( k = 1 ... N k = 1 \dots N k=1...N)，把它作为"中转站"，看看经过点 k k k 是否能缩短点 i i i 到点 j j j 的距离。

    状态转移方程 ：
    d G ( i , j ) = min ⁡ { d G ( i , j ) , d G ( i , k ) + d G ( k , j ) } d_G(i,j) = \min \{ d_G(i,j), \quad d_G(i,k) + d_G(k,j) \} dG(i,j)=min{dG(i,j),dG(i,k)+dG(k,j)}

Python 代码实现 (Floyd-Warshall)

python 复制代码 
import numpy as np

def floyd_warshall(dist_matrix):
    """
    Args:
        dist_matrix: N x N 邻接矩阵 (不相连处为 inf)
    Returns:
        d: N x N 全局测地线距离矩阵
    """
    N = dist_matrix.shape[0]
    d = dist_matrix.copy()
    
    # 三层循环：k 为中转点
    for k in range(N):
        for i in range(N):
            for j in range(N):
                # 状态转移
                if d[i, k] + d[k, j] < d[i, j]:
                    d[i, j] = d[i, k] + d[k, j]
    return d

  • 复杂度分析

    • 时间复杂度： O ( N 3 ) O(N^3) O(N3)。

      因为有三层循环（ k , i , j k, i, j k,i,j 都要从 1 遍历到 N N N）。

      这也是 Isomap 最大的瓶颈。如果数据点有 10,000 个， 10000 3 10000^3 100003 是一个天文数字，计算会非常慢。

    • 空间复杂度： O ( N 2 ) O(N^2) O(N2)。

      需要存储一个 N × N N \times N N×N 的稠密距离矩阵。

Step 3: 构建低维嵌入 (MDS Embedding)

Isomap 的最后一步是使用 经典 MDS (Classical MDS) 将测地线距离矩阵 D G D_G DG 转化为低维坐标 Y = [ y 1 , y 2 , ... , y N ] T ∈ R N × d \mathbf{Y} = [y_1, y_2, \dots, y_N]^T \in \mathbb{R}^{N \times d} Y=[y1,y2,...,yN]T∈RN×d（对应图 3C）。

核心问题是：已知点之间的距离（Step 3通过遍历求出来的），如何反求点的坐标？

1. 设定目标与假设

假设我们寻找的低维坐标 y i y_i yi 满足欧氏距离等于测地线距离：
∥ y i − y j ∥ 2 = D G ( i , j ) 2 \|y_i - y_j\|^2 = D_G(i,j)^2 ∥yi−yj∥2=DG(i,j)2

为了得到唯一解，我们必须消除平移不确定性，假设数据的重心在原点 ：
∑ i = 1 N y i = 0 \sum_{i=1}^N y_i = \mathbf{0} i=1∑Nyi=0

解释： 这是我们自己设定的，也就是说所有的点去中心化

2. 从距离到内积 (The Law of Cosines)

我们需要将"距离矩阵"转换为"内积矩阵"才能进行特征分解。

展开欧氏距离的平方：
D i j 2 = ∥ y i − y j ∥ 2 = ( y i − y j ) T ( y i − y j ) = y i T y i + y j T y j − 2 y i T y j = ∥ y i ∥ 2 + ∥ y j ∥ 2 − 2 ⟨ y i , y j ⟩ \begin{aligned} D_{ij}^2 &= \|y_i - y_j\|^2 \\ &= (y_i - y_j)^T (y_i - y_j) \\ &= y_i^T y_i + y_j^T y_j - 2 y_i^T y_j \\ &= \|y_i\|^2 + \|y_j\|^2 - 2 \langle y_i, y_j \rangle \end{aligned} Dij2=∥yi−yj∥2=(yi−yj)T(yi−yj)=yiTyi+yjTyj−2yiTyj=∥yi∥2+∥yj∥2−2⟨yi,yj⟩

令内积矩阵 B \mathbf{B} B 的元素为 B i j = ⟨ y i , y j ⟩ = y i T y j B_{ij} = \langle y_i, y_j \rangle = y_i^T y_j Bij=⟨yi,yj⟩=yiTyj。

则上式变为：
D i j 2 = B i i + B j j − 2 B i j (公式 1) D_{ij}^2 = B_{ii} + B_{jj} - 2 B_{ij} \text{(公式 1)} Dij2=Bii+Bjj−2Bij(公式 1)

现在我们遇到了困难： D i j 2 D_{ij}^2 Dij2 是已知的（Step 2 算出来的），但 B i i , B j j , B i j B_{ii}, B_{jj}, B_{ij} Bii,Bjj,Bij 都是未知的。一个方程解三个未知数？

3. 双中心化 (Double Centering)

为了消掉 B i i B_{ii} Bii 和 B j j B_{jj} Bjj，我们利用重心为 0 的性质（即 ∑ B i j = 0 \sum B_{ij} = 0 ∑Bij=0）。我们对距离矩阵进行"行平均"和"列平均"操作。

定义算子：

  • 1 N ∑ j = 1 N D i j 2 \frac{1}{N} \sum_{j=1}^N D_{ij}^2 N1∑j=1NDij2 （第 i i i 行的平均）
  • 1 N ∑ i = 1 N D i j 2 \frac{1}{N} \sum_{i=1}^N D_{ij}^2 N1∑i=1NDij2 （第 j j j 列的平均）
  • 1 N 2 ∑ i = 1 N ∑ j = 1 N D i j 2 \frac{1}{N^2} \sum_{i=1}^N \sum_{j=1}^N D_{ij}^2 N21∑i=1N∑j=1NDij2 （全矩阵平均）

对 (公式 1) 进行复杂的求和与平均运算后（利用 ∑ y i = 0 \sum y_i = 0 ∑yi=0 使得 ∑ B i ⋅ = 0 \sum B_{i \cdot} = 0 ∑Bi⋅=0），我们会神奇地发现：
B i j = − 1 2 ( D i j 2 − 1 N ∑ k D i k 2 − 1 N ∑ k D k j 2 + 1 N 2 ∑ k , l D k l 2 ) (公式 2) B_{ij} = -\frac{1}{2} \left( D_{ij}^2 - \frac{1}{N}\sum_k D_{ik}^2 - \frac{1}{N}\sum_k D_{kj}^2 + \frac{1}{N^2}\sum_{k,l} D_{kl}^2 \right) \text{(公式 2)} Bij=−21 Dij2−N1k∑Dik2−N1k∑Dkj2+N21k,l∑Dkl2 (公式 2)

矩阵形式 (最优雅的表达) ：

令 S \mathbf{S} S 为平方距离矩阵 ( S i j = D i j 2 S_{ij} = D_{ij}^2 Sij=Dij2)，令 H = I − 1 N 11 T \mathbf{H} = \mathbf{I} - \frac{1}{N}\mathbf{1}\mathbf{1}^T H=I−N111T 为中心化矩阵。上述繁琐的加减运算等价于：

B = − 1 2 H S H (公式 3) \mathbf{B} = -\frac{1}{2} \mathbf{H} \mathbf{S} \mathbf{H} \text{(公式 3)} B=−21HSH(公式 3)

这就是为什么公式里会有 − 1 / 2 -1/2 −1/2 和那个奇怪的矩阵乘法。它的物理意义是：从距离平方中剔除行均值和列均值，剩下的就是纯粹的内积信息。

解释： 由公式2推导公式3不好推，但是由公式3推导公式2很简单

首先，定义一个全 1 的矩阵 J \mathbf{J} J（为了方便书写，用 J \mathbf{J} J 代表那一坨平均算子）：
J = 1 N 11 T = ( 1 / N ⋯ 1 / N ⋮ ⋱ ⋮ 1 / N ⋯ 1 / N ) \mathbf{J} = \frac{1}{N}\mathbf{1}\mathbf{1}^T = \begin{pmatrix} 1/N & \cdots & 1/N \\ \vdots & \ddots & \vdots \\ 1/N & \cdots & 1/N \end{pmatrix} J=N111T= 1/N⋮1/N⋯⋱⋯1/N⋮1/N

这个矩阵 J \mathbf{J} J 有个特性：任何矩阵乘以它，就是在算平均值。

J S \mathbf{J}\mathbf{S} JS： J \mathbf{J} J在左求列平均
S J \mathbf{S}\mathbf{J} SJ： J \mathbf{J} J在右求行平均
J S J \mathbf{J}\mathbf{S}\mathbf{J} JSJ：左右都有 J \mathbf{J} J，整个矩阵变为平均值

那么，中心化矩阵 H \mathbf{H} H 就可以写成：
H = I − J \mathbf{H} = \mathbf{I} - \mathbf{J} H=I−J

暴力展开 H S H \mathbf{H}\mathbf{S}\mathbf{H} HSH

现在我们将 H = I − J \mathbf{H} = \mathbf{I} - \mathbf{J} H=I−J 代入 H S H \mathbf{H}\mathbf{S}\mathbf{H} HSH 并进行乘法分配（就像做 ( a − b ) × ( a − b ) (a-b)\times(a-b) (a−b)×(a−b) 一样）：

H S H = ( I − J ) S ( I − J ) = ( S − J S ) ( I − J ) <-- 先把左边乘进去 = S − S J − J S + J S J <-- 再把右边乘进去 \begin{aligned} \mathbf{H}\mathbf{S}\mathbf{H} &= (\mathbf{I} - \mathbf{J}) \mathbf{S} (\mathbf{I} - \mathbf{J}) \\ &= (\mathbf{S} - \mathbf{J}\mathbf{S}) (\mathbf{I} - \mathbf{J}) \quad \text{<-- 先把左边乘进去} \\ &= \mathbf{S} - \mathbf{S}\mathbf{J} - \mathbf{J}\mathbf{S} + \mathbf{J}\mathbf{S}\mathbf{J} \quad \text{<-- 再把右边乘进去} \end{aligned} HSH=(I−J)S(I−J)=(S−JS)(I−J)<-- 先把左边乘进去=S−SJ−JS+JSJ<-- 再把右边乘进去

解释： 令 S \mathbf{S} S 为平方距离矩阵 ( S i j = D i j 2 S_{ij} = D_{ij}^2 Sij=Dij2)带入到上面的这个公式就得到公式2了，一般也不用推导，记住公式3能够求内积矩阵就可以了

4. 特征分解求坐标

现在我们有了内积矩阵 B \mathbf{B} B。根据定义 B = Y Y T \mathbf{B} = \mathbf{Y} \mathbf{Y}^T B=YYT。

因为 B \mathbf{B} B 是对称半正定矩阵，我们可以对其进行特征值分解 (Eigendecomposition)：
B = V Λ V T \mathbf{B} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^T B=VΛVT

其中 Λ = diag ( λ 1 , ... , λ N ) \mathbf{\Lambda} = \text{diag}(\lambda_1, \dots, \lambda_N) Λ=diag(λ1,...,λN) 是特征值（从大到小排列）， V \mathbf{V} V 是特征向量矩阵。

为了降维到 d d d 维，我们只取前 d d d 个最大的正特征值：
B ≈ V d Λ d V d T = ( V d Λ d 1 / 2 ) ( V d Λ d 1 / 2 ) T \mathbf{B} \approx \mathbf{V}_d \mathbf{\Lambda}_d \mathbf{V}_d^T = (\mathbf{V}_d \mathbf{\Lambda}_d^{1/2}) (\mathbf{V}_d \mathbf{\Lambda}_d^{1/2})^T B≈VdΛdVdT=(VdΛd1/2)(VdΛd1/2)T

对比 B = Y Y T \mathbf{B} = \mathbf{Y} \mathbf{Y}^T B=YYT，我们可以直接读出坐标 Y \mathbf{Y} Y：
Y = V d Λ d 1 / 2 \mathbf{Y} = \mathbf{V}_d \mathbf{\Lambda}_d^{1/2} Y=VdΛd1/2

即第 i i i 个点的第 k k k 维坐标为：
y i k = λ k ⋅ v i k y_{ik} = \sqrt{\lambda_k} \cdot v_{ik} yik=λk ⋅vik

至此，我们成功从距离矩阵 D G D_G DG 还原出了低维坐标 Y \mathbf{Y} Y。

解释： 你想要几维，就取前几个就可以了

4. 补充只是：切空间距离 (Tangent Distance) 的计算细节

在 Isomap 处理手写数字时，为了解决"旋转/缩放不变性"问题，Simard 等人提出了切空间距离。这不只是一个概念，更是一套严密的数学计算流程。以下是 Step-by-Step 的计算指南：

第一步：准备"原材料" (计算图像梯度)

首先，我们要知道图片怎么"动"。图片是由像素组成的矩阵 I I I（例如 MNIST 为 28 × 28 28 \times 28 28×28）。

要让图片动起来（比如平移），我们需要知道每个像素"旁边"是什么颜色。这就叫梯度。

  • 输入 ：图片矩阵 I I I ( 28 × 28 28 \times 28 28×28)。
  • 操作 ：算出两个新矩阵：
    1. 水平梯度图 ( I x I_x Ix) ：每个像素和它右边 像素的差值。
      直觉：这里记录了竖直边缘（哪里变亮或变暗了）。
    2. 垂直梯度图 ( I y I_y Iy) ：每个像素和它下边 像素的差值。
      直觉：这里记录了水平边缘。

直观例子（假设图片只有一行）：

  • 像素值：[10, 10, 100, 10, 10] （中间有个亮点）
  • 梯度 I x I_x Ix：[0, 90, -90, 0] （左边陡升，右边陡降）
  • 含义*：告诉计算机，如果想把亮点往右移，左边像素要 + 90 +90 +90 (变亮)，右边像素要 − 90 -90 −90 (变暗)。
第二步：制造"变形工具包" (生成 7 个切向量)

这是最关键的一步。我们为数字设计了 7 种标准变形，并计算每种变形对应的"变化趋势图"（切向量）。

设定坐标系：图片中心为原点 ( 0 , 0 ) (0,0) (0,0)。

我们需要计算 7 个 28 × 28 28 \times 28 28×28 的矩阵，并将它们拉直为 784 × 1 784 \times 1 784×1 的向量：

变形类型 切向量公式 物理含义解释
X轴平移 ( T 1 T_1 T1) T 1 = I x T_1 = I_x T1=Ix 直接利用水平梯度。
Y轴平移 ( T 2 T_2 T2) T 2 = I y T_2 = I_y T2=Iy 直接利用垂直梯度。
旋转 ( T 3 T_3 T3) T 3 = y ⋅ I x − x ⋅ I y T_3 = y \cdot I_x - x \cdot I_y T3=y⋅Ix−x⋅Iy 角动量公式。描述旋转时的像素变化。
缩放 ( T 4 T_4 T4) T 4 = x ⋅ I x + y ⋅ I y T_4 = x \cdot I_x + y \cdot I_y T4=x⋅Ix+y⋅Iy 放大时，四周像素向外扩散。
平行挤压 ( T 5 T_5 T5) T 5 = x ⋅ I x − y ⋅ I y T_5 = x \cdot I_x - y \cdot I_y T5=x⋅Ix−y⋅Iy 保持面积不变，拉长或压扁。
对角挤压 ( T 6 T_6 T6) T 6 = y ⋅ I x + x ⋅ I y T_6 = y \cdot I_x + x \cdot I_y T6=y⋅Ix+x⋅Iy 沿对角线方向拉伸。
笔画加粗 ( T 7 T_7 T7) T 7 = ( I x ) 2 + ( I y ) 2 T_7 = (I_x)^2 + (I_y)^2 T7=(Ix)2+(Iy)2 近似公式。边缘梯度大的地方变亮，模拟笔画变粗。

做完这一步，对于图片 A，我们得到了一个矩阵 T A \mathbf{T}_A TA ( 784 × 7 784 \times 7 784×7)；对于图片 B，得到矩阵 T B \mathbf{T}_B TB ( 784 × 7 784 \times 7 784×7)。

第三步：让它们"对战" (建立最小二乘方程)

现在我们想问：

"如果让 A 变一点点 ( T A ⋅ α \mathbf{T}_A \cdot \alpha TA⋅α)，让 B 也变一点点 ( T B ⋅ β \mathbf{T}_B \cdot \beta TB⋅β)，它俩能撞上吗？"

数学目标是寻找系数向量 α \alpha α (7维) 和 β \beta β (7维)，使得变形后的误差最小：
Loss = ∥ ( Img A + T A ⋅ α ) − ( Img B + T B ⋅ β ) ∥ 2 \text{Loss} = \| (\text{Img}_A + \mathbf{T}_A \cdot \alpha) - (\text{Img}_B + \mathbf{T}_B \cdot \beta) \|_2 Loss=∥(ImgA+TA⋅α)−(ImgB+TB⋅β)∥2

为了让计算机求解，我们将其整理成标准的线性方程组形式 M x = b \mathbf{M}x = b Mx=b：

  1. 大矩阵 M \mathbf{M} M ：将 T A \mathbf{T}_A TA 和 − T B -\mathbf{T}_B −TB 左右拼接。
    M = [ T A , − T B ] ( 维度 : 784 × 14 ) \mathbf{M} = [\mathbf{T}_A, -\mathbf{T}_B] \quad (\text{维度}: 784 \times 14) M=[TA,−TB](维度:784×14)
  2. 目标向量 b b b ：两张图片的原始差值。
    b = Img B − Img A b = \text{Img}_B - \text{Img}_A b=ImgB−ImgA
第四步：求解与距离计算

直接调用线性代数库（如 numpy.linalg.lstsq）求解 M x = b \mathbf{M}x = b Mx=b。

  • 得到最优解 x ∗ x^* x∗ 后，计算残差：
    Tangent Distance = ∥ M x ∗ − b ∥ 2 \text{Tangent Distance} = \| \mathbf{M}x^* - b \|_2 Tangent Distance=∥Mx∗−b∥2

结论：这个残差就是 Isomap 使用的最终距离。即便原始像素差很大，只要能通过旋转/缩放对齐，这个距离就会很小，从而正确判定它们是"邻居"。

5. 实验结果：图 4 的流形插值

图 4 (Interpolation) 是论文中最直观展示"流形学习成果"的部分。

实验怎么做的？

  1. Isomap 已经把所有图片映射到了低维空间（比如二维平面）。
  2. 在低维平面上，任选两个点（代表两个看起来很不一样的数字或人脸）。
  3. 在两点之间画一条直线。
  4. 在直线上均匀取点，然后通过最近邻查找 (Nearest Neighbor)，找到数据集中对应的高维原始图像。

结果说明了什么？

  • 平滑过渡 ：观察图 4，你会发现从起点到终点，图像的变化是连续的、符合逻辑的。
    • 例如：数字 "2" 的圆圈是逐渐变小 直到消失的；人脸是慢慢转过去的。
  • 对比线性方法：如果在像素空间直接做线性插值（Linear Interpolation），你会看到两张图重叠在一起的"鬼影" (Ghosting)。
  • 结论 ：这证明了 Isomap 展开的低维空间是凸的 (Convex) 且 连续的。算法成功学会了数据的内在生成流形，这里的"直线"真正对应了物理意义上的"渐变"。

6. 讨论与评价

Isomap 的历史地位

它是第一个计算效率高、且具有全局最优保证的非线性降维算法。它不需要像神经网络那样调参、防过拟合，它的结果是确定性的。

优点：

  1. 捕捉非线性：能处理瑞士卷、莫比乌斯带等复杂结构。
  2. 全局最优：基于特征值分解，一定能找到全局最优解。
  3. 极简美学：只有三个步骤，逻辑清晰。

缺点：

  1. 计算瓶颈 ：Step 2 的最短路径计算复杂度是 O ( N 3 ) O(N^3) O(N3)，这在 2000 年限制了数据规模（几千个点），虽然现在有 L-Isomap 等加速版本，但对百万级数据仍显吃力。
  2. 短路效应 (Short-circuiting)：这是基于图论方法的通病。如果噪音导致流形上本来很远的两层被错误地连了一根边，整个流形结构会瞬间崩塌。
  3. 拓扑限制：MDS 强行把流形铺在欧氏空间上。如果流形本身是闭合的（比如一个球体），硬把它撕开铺平会造成极大的扭曲。

总结

Isomap 是一次几何学与统计学习的完美结合。它提醒我们，在处理高维数据时，不要被表象迷惑，要学会寻找那个卷曲的、低维的、真实的"流形"。

💬 互动话题 ：

Isomap 的"测地线"思想在现在的图神经网络 (GNN) 或 3D 视觉中是否还有影子？欢迎在评论区讨论！

📚 附录：点云网络系列导航

🔥 欢迎订阅专栏 ：【流形研读：经典与前沿论文精讲】持续更新中...

本文为 CSDN 专栏【流形研读：经典与前沿论文精讲】原创内容，转载请注明出处。。

相关推荐
羑悻的小杀马特2 小时前
零成本神器组合：用Docker+Uptime Kuma+cpolar打造永不掉线的远程监控系统！
运维·人工智能·docker·容器
mjhcsp2 小时前
莫比乌斯反演总结
c++·算法
龙山云仓2 小时前
No132:AI中国故事-对话老子——道法自然与AI设计：无为而治、柔弱胜刚强与复杂系统智慧
大数据·人工智能·机器学习
Data-Miner2 小时前
类似Pandas AI的几个数据分析处理智能体介绍
人工智能·数据分析·pandas
TonyLee0172 小时前
新型学习范式（机器学习）
人工智能·学习·机器学习
Deepoch2 小时前
Deepoc具身大模型居家机器人：重新定义家庭智能服务新标准
人工智能·机器人·具身模型·deepoc·居家机器人·居家好物·智能居家
ucancode2 小时前
AI --＞ Mermaid --＞ 图形可视化 （UI）
人工智能·ui·ai·mermaid
小李AI飞刀^_^2 小时前
AlphaEarth Foundations：面向全球尺度的嵌入场模型
人工智能
KmBase2 小时前
【AI】从同构到多态：AGI的可能之路
人工智能·agi
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Claude Code Skills 实用使用手册04UV安装并设置国内源05BongoCat - 跨平台键盘猫动画工具06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07Linux下V2Ray安装配置指南08安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）09Open Code教程（四）| 高级配置与集成10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南