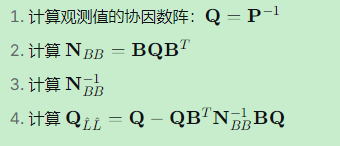条件平差中的精度评定详解
一、精度评定的总体框架
在条件平差中，精度评定是平差过程中至关重要的环节，它回答了一个核心问题：
经过平差处理后，我们得到的平差值
以及由其构成的函数究竟有多可靠？
精度评定的目标是通过数学方法量化平差结果的不确定性，为实际应用提供质量指标。
二、条件平差精度评定的三大任务
任务1：评定单位权观测值的精度
1.1 单位权方差估值的计算
1.3 几何解释
任务2：
几何意义：
任务3：评定平差值函数的精度
3.1 平差值函数的概念
在实际应用中，我们关心的往往不是单个观测量的平差值，而是它们的函数，例如：
-
水准网中某点的高程（是高差的函数）
-
三角网中某边的边长（是角度的函数）
-
GNSS中某点的坐标（是观测值的函数）
设平差值的函数为：
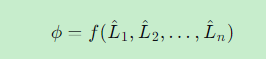
3.2 线性函数情况
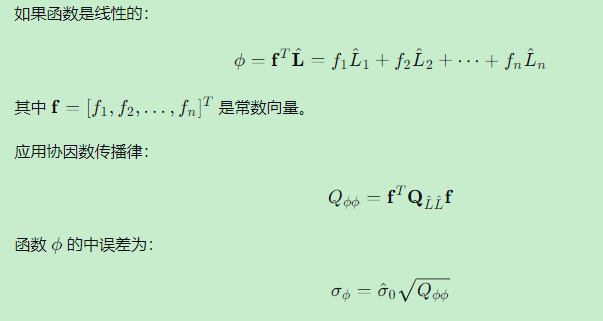
3.3 非线性函数情况
3.4 权函数式的概念
下面是自己学习时的笔记：
下面笔记公式来源参考：https://blog.csdn.net/zx642288904/article/details/156730854?spm=1011.2415.3001.5331
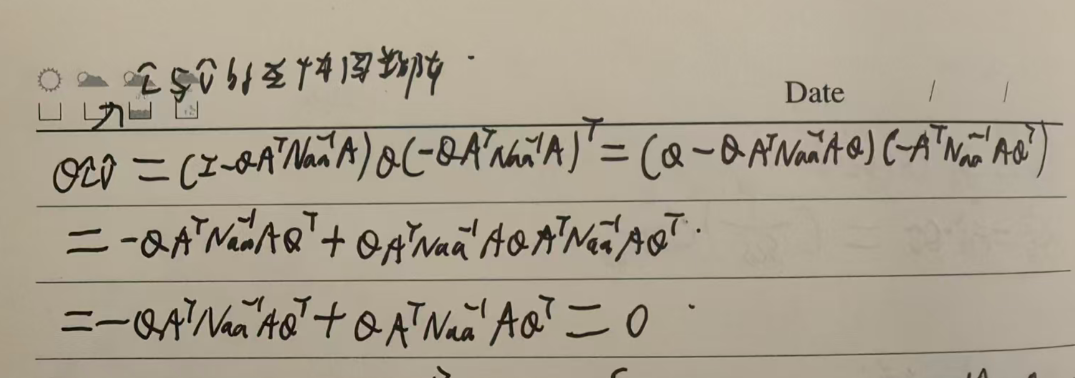
三、条件平差精度评定的完整流程
步骤1：计算单位权中误差
步骤2：计算平差值的协因数阵
步骤3：计算平差值的中误差
步骤4：评定平差值函数的精度
四、示例：水准网条件平差的精度评定
4.1 问题描述
已知水准网如图所示，A为已知点，H_A = 10.000mHA=10.000m，观测了3条路线的高差：
-
路线1：A→B，h_1 = +2.500mh1=+2.500m，路线长 S_1 = 2kmS1=2km
-
路线2：B→C，h_2 = +1.000mh2=+1.000m，路线长 S_2 = 1kmS2=1km
-
路线3：A→C，h_3 = +3.498mh3=+3.498m，路线长 S_3 = 3kmS3=3km
4.2 条件平差计算回顾
4.3 精度评定计算
1. 单位权中误差
2. 平差值 \hat{\mathbf{h}}h^ 的协因数阵
4. C点高程的精度评定
C点高程可以通过两条路线计算：
函数的协因数：
C点高程的中误差：
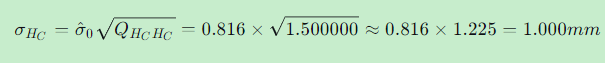
五、条件平差精度评定的特点
5.1 与间接平差精度评定的比较
5.2 精度评定的几何意义
在条件平差中，精度评定的几何意义可以理解为：
-
单位权中误差：反映了观测系列的整体质量
-
平差值协因数阵：描述了平差值的不确定性"椭球"
-
函数的中误差：给出了特定量的可靠性指标
5.3 精度评定的实际意义
-
质量控制 ：通过
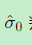判断观测质量 -
可靠性评估：为测量结果提供可信度指标
-
工程决策：根据精度决定测量成果是否满足要求
-
优化设计：指导后续测量工作的布设
六、总结与要点
6.1 条件平差精度评定的核心公式
6.2 关键理解点
-
精度评定必须在平差计算完成后进行
-
单位权中误差是基准，所有其他精度都以此为参照
-
平差值的精度一定不低于原始观测值的精度
-
函数精度的评定需要正确的权函数式
-
精度评定结果是统计意义上的，不是绝对保证
6.3 对AGNSS开发者的意义
虽然现代GNSS数据处理主要采用间接平差，但理解条件平差的精度评定有助于：
-
深入理解精度传播的本质
-
掌握不同平差方法间的内在联系
-
在特定情况下（如已知几何条件强烈时）选择合适方法
-
为算法验证提供交叉检查的手段
精度评定是测量平差的灵魂，它让测量成果从"一个数值"变成了"带有质量信息的可靠数据"。掌握条件平差的精度评定，是全面理解测量数据处理理论的重要一步。
单位权中误差作为精度评定基准的原因及其估值公式的推导
一、为什么单位权中误差是精度评定的基准？
1.1 权的相对性与基准的必要性
1.2 平差结果精度的统一表达
1.3 在条件平差中的具体体现
在条件平差中：
二、单位权方差估值公式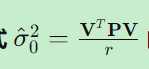 
的推导与理解
2.1 基本假设与模型
考虑一般平差问题（以条件平差为例）：
2.2 改正数 V 的统计性质
2.3 二次型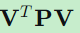 
的期望
2.4 单位权方差的无偏估计
2.5 自由度的直观解释
分母 r 是多余观测数（条件方程个数），它代表了：
-
用于检核和控制误差的"多余信息"的数量
-
可以自由变动的残差分量的个数
从线性代数角度看：
三、公式的进一步讨论与注意事项
3.1 与间接平差的统一性
在间接平差（参数平差）中，有完全类似的公式：
3.2 公式的统计分布
3.3 实际应用中的意义
3.4 示例验证
四、总结
4.1 单位权中误差作为基准的原因
-
权的相对性：权只表示相对精度，需要绝对基准才能得到实际精度。
-
统一表达 ：所有平差量的精度都通过
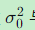与各自的协因数阵相乘得到。 -
可传递性 ：通过
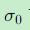可以将观测值的精度传递给平差值及其函数。
4.2 单位权方差估值公式的理论依据
-
无偏性 ：在观测误差无偏、权阵正确的假设下，
-
自由度匹配：分母 rr 是多余观测数，代表了用于估计误差的自由度。
-
统计最优性：在正态误差假设下，该估计量具有良好的统计性质。
4.3 对AGNSS开发的指导意义
在GNSS数据处理中：
-
单位权中误差的估值可用于判断当前观测时段的质量。
-
通过分析
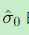的变化，可以检测观测条件的变化（如多路径效应、电离层扰动等）。 -
该公式是各种精度指标（如DOP值、定位精度）计算的基础。
理解单位权中误差的基准作用和估值公式的推导，不仅有助于深入掌握测量平差理论，也为在实际GNSS系统开发中设计合理的精度评定算法提供了理论基础。