Batched Matrix Multiplication

图中前面的 (b1,b2b_1, b_2b1,b2) 表示 批次维度(batch dimensions) ,也就是"有多少个矩阵同时在做乘法"。在 batched matrix multiplication 中,最后两维 (n,m) 与 (m,p) 按普通矩阵乘法规则相乘,而前面所有维度 (这里是 b1,b2b_1, b_2b1,b2)并不参与数值运算,只用于索引不同的矩阵批次;它们必须相等或满足广播规则,结果中这些维度会被原样保留下来.
Broadcasting
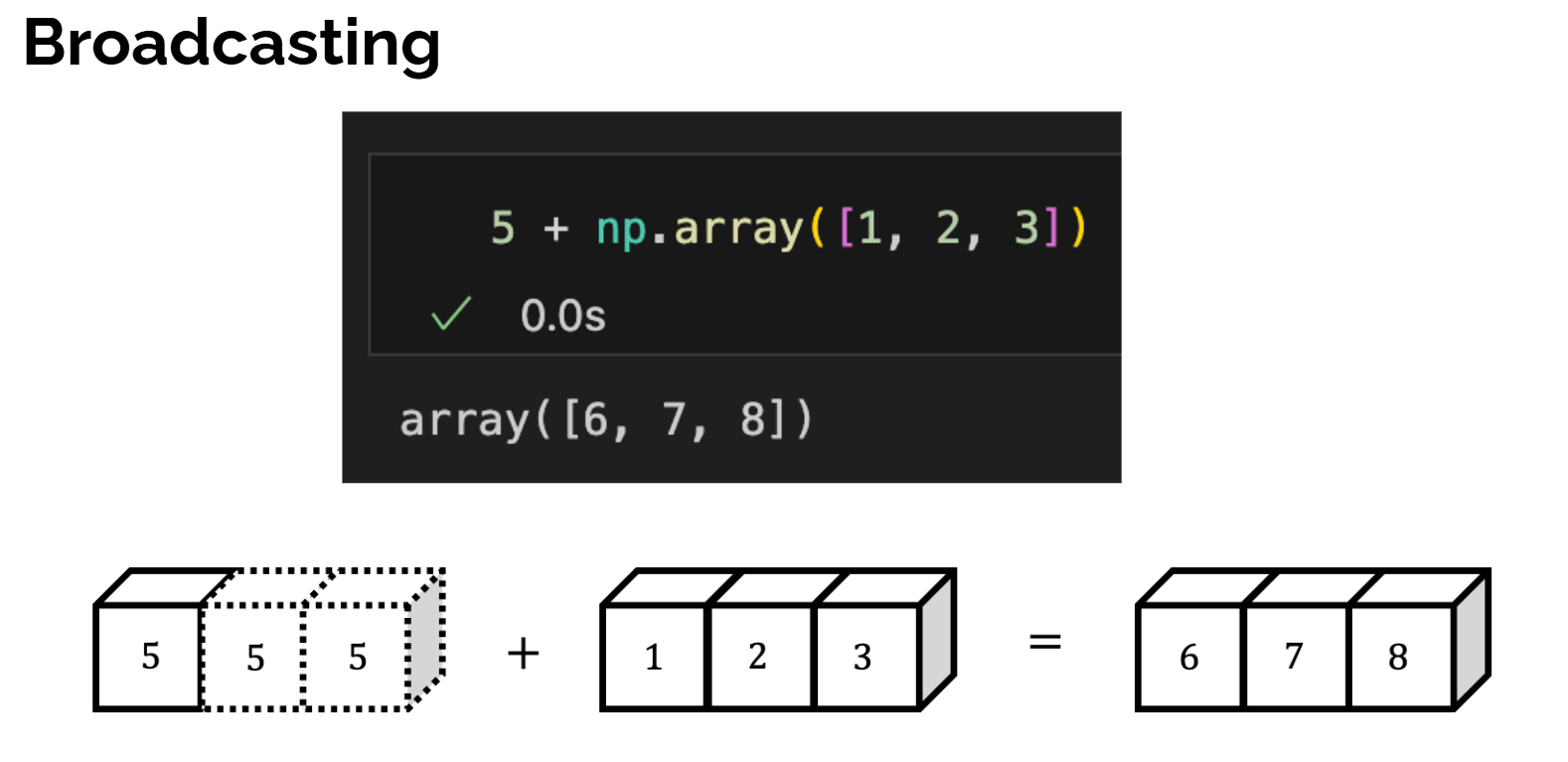
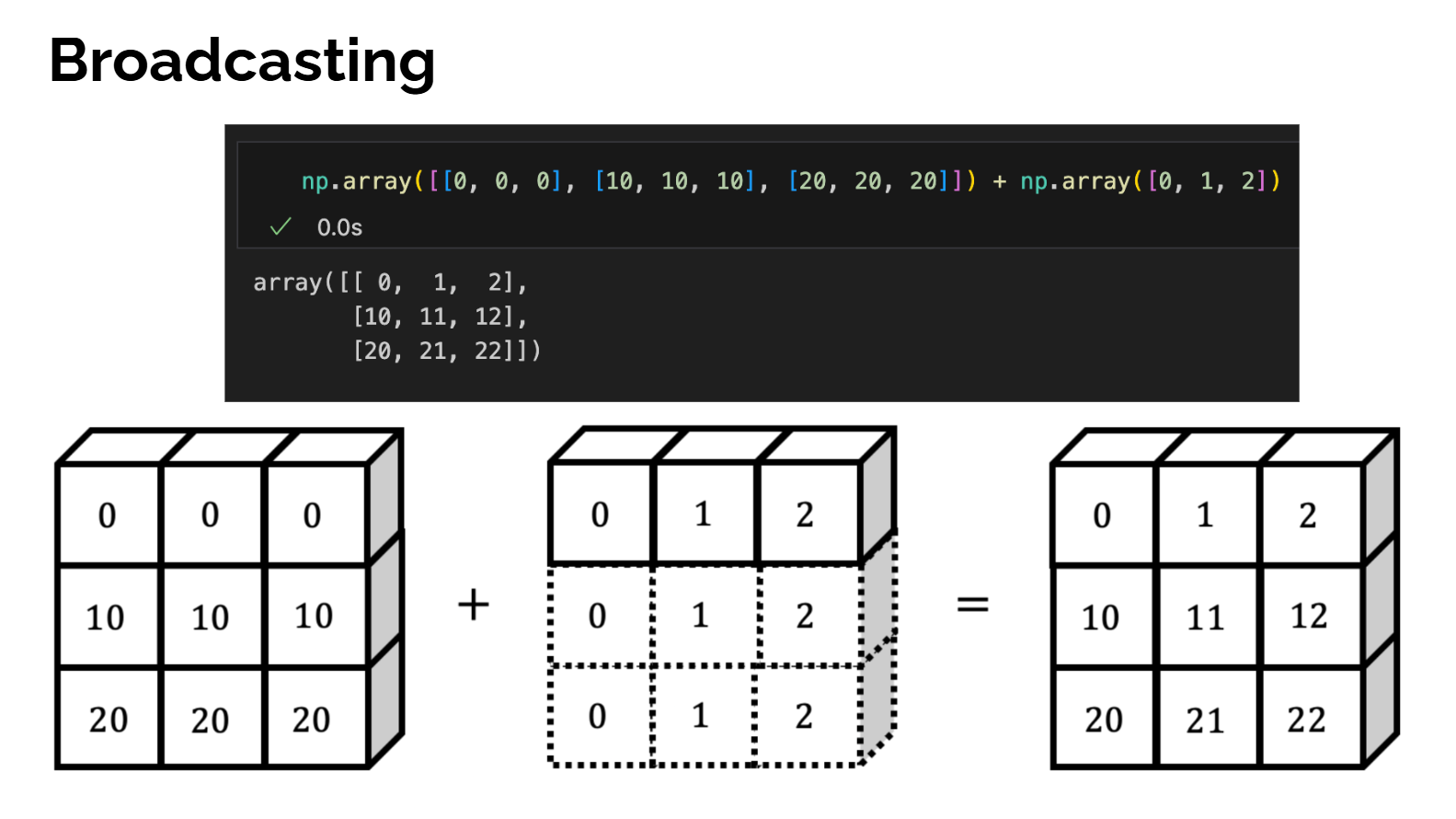
我们允许矩阵与向量直接相加 ,虽然在线性代数的严格定义里这本来是未定义的操作;具体做法是规定结果矩阵 C 的每个元素满足 Cx,y=Ax,y+byC_{x,y}=A_{x,y}+b_yCx,y=Ax,y+by,也就是说向量 b 被当作在行方向上复制,加到矩阵 A 的每一行上,从而得到一个同形状的矩阵,而无需显式构造一个"每一行都等于 b"的大矩阵
规则

第 1 条(右到左比较维度)
If the two arrays differ in their number of dimensions, the shape of the one with fewer dimensions is padded with ones on its leading (left) side.
意思是:如果两个数组的维度数不同 ,就先把"维度少的那个"在左边补 1 ,直到两个数组的维度数一样;注意这是概念上的补 1,不是实际创建新数据。例如形状 (n,) 和 (b,n) 比较时,把 (n,) 看成 (1,n)。
第 2 条(维度为1的拉伸)
If the shape of the two arrays does not match in any dimension, the array with shape equal to 1 in that dimension is stretched to match the other shape.
意思是:在某一个维度上,如果两个数组大小不同,但其中一个等于 1,那么这个等于 1 的维度会被**拉伸(复制)**到和另一个一样大;这就是"广播"的核心。例如 (1,n) 和 (b,n) 运算时,前者会在第一个维度被复制 (b) 次。
第 3 条
If in any dimension the sizes disagree and neither is equal to 1, an error is raised.
意思是:如果在某个维度上两个大小不相等 ,而且都不等于 1,那就没法广播,运算直接报错;例如 (2,n) 和 (3,n) 在第一维上既不相等又都不为 1,因此是非法的。
举例子(维度循环有点问题)
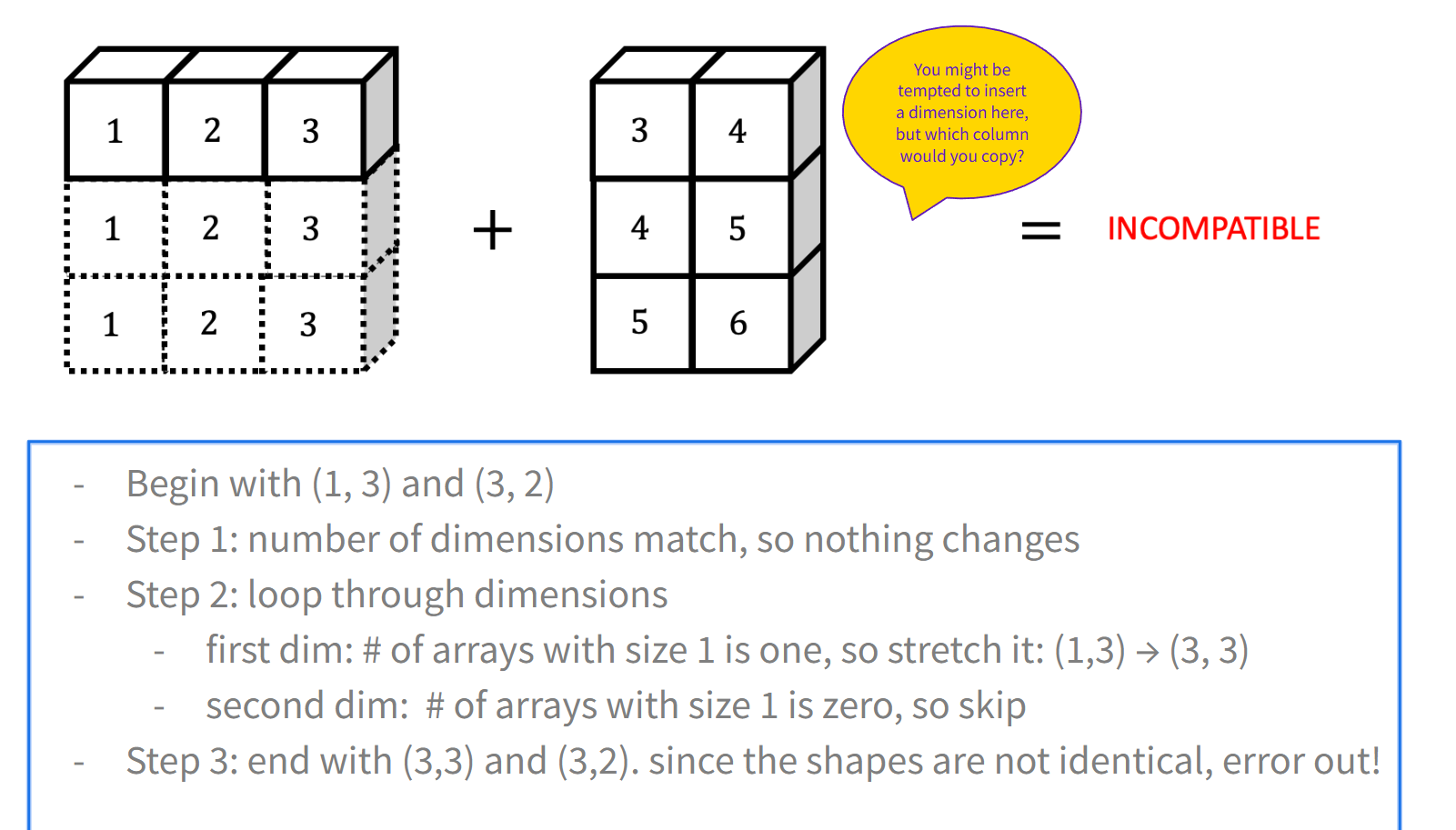
右对齐 → 逐轴检查 → 有 1 就拉伸 → 否则报错
例题

