Abastract
生成建模可以表述为学习一个映射 (f),使得其对输入分布的推前(pushforward)分布 能够匹配真实数据分布。在推理阶段,这种推前过程通常需要迭代执行,例如扩散模型或基于流的模型。本文提出一种新的范式,称为漂移模型(Drifting Models) :它在训练过程中不断演化推前分布,并天然支持一步推理(one-step inference)。我们引入一个漂移场(drifting field)来控制样本的移动,当生成分布与数据分布一致时系统达到平衡。由此得到一个训练目标,使得神经网络优化器能够在训练期间推动分布逐步演化。实验结果表明,我们的一步生成器在 ImageNet 256×256 上取得了当前最优的效果:在潜空间(latent space)中 FID 达到 1.54,在像素空间(pixel space)中 FID 达到 1.61。我们希望这项工作能为高质量的一步生成开辟新的可能性。
1. Introduction
生成模型通常被认为比判别模型更具挑战性。判别模型通常侧重于将单个样本映射到其对应的标签,而生成模型则关注从一个分布到另一个分布的映射。这可以表述为学习一个映射函数 \( f \),使得先验分布的推前分布与数据分布相匹配,即
。从概念上讲,生成模型学习的是一个将函数(此处为分布)映射到另一个函数的泛函(此处为
)。
"推前"行为可以在推理阶段以迭代方式实现,例如在扩散模型(Sohl-Dickstein 等人,2015)和流匹配(Lipman 等人,2022)等主流范式中。在生成过程中,这些模型将含噪声较多的样本映射至略微干净的样本,使样本分布逐步向数据分布演化。这种建模理念可被视为将一个复杂的推前映射(即)分解为一系列更易实现的变换,并在推理阶段逐步应用。
在本文中,我们提出了一种新的生成建模范式------漂移模型。该模型的核心特点是学习一个在**训练期间**动态演化的推前映射,从而避免了迭代式推理过程的需求。映射 f 通过一个单步前向、非迭代的网络实现。由于深度学习优化过程本质上是迭代的,我们可以很自然地将训练过程视为通过不断更新 f 来推动其推前分布 逐步演化(见图1)。
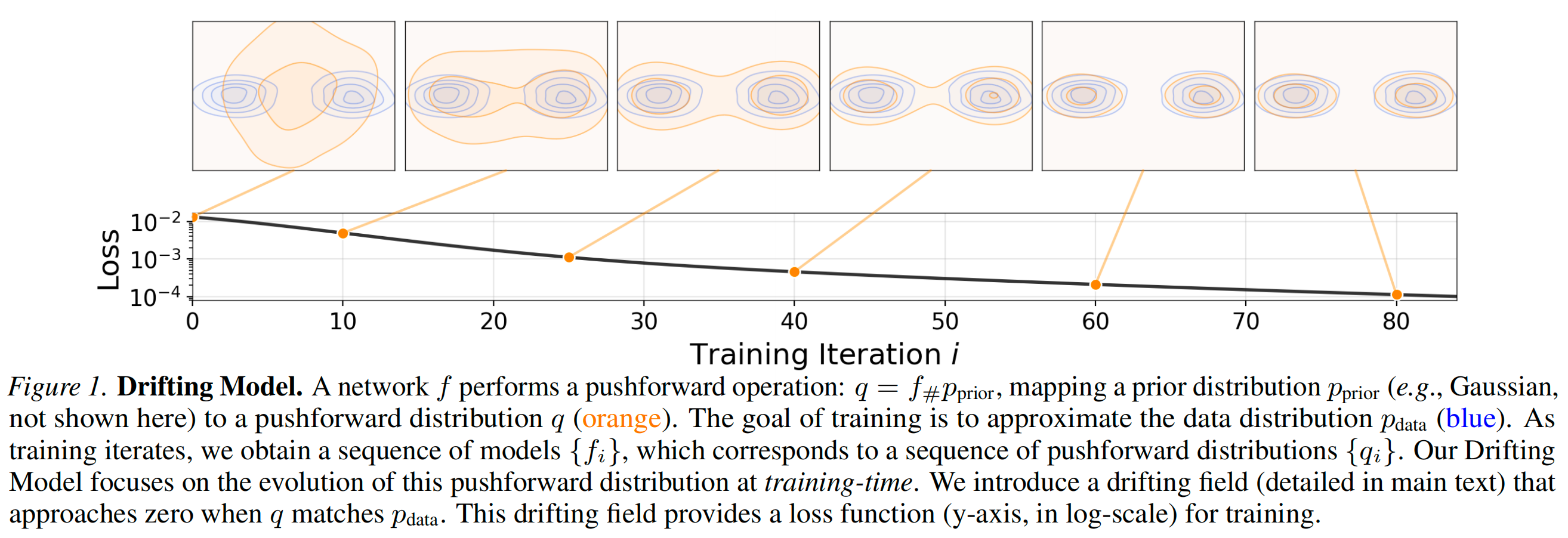
为驱动训练时推前分布的演化,我们引入了一个漂移场来控制样本的运动。该漂移场依赖于生成分布与数据分布。根据定义,当这两个分布匹配时,该场将趋于零,从而达成一种**均衡状态**------此时样本不再发生漂移。
基于这一理论框架,我们提出了一种简单的训练目标------**最小化生成样本的漂移量**。该目标通过诱导样本运动,从而在迭代优化(例如随机梯度下降)过程中推动底层的推前分布持续演化。我们进一步阐述了漂移场的设计、神经网络模型的结构以及完整的训练算法。
漂移模型天然地实现了单步("1-NFE")生成,并取得了强劲的实验性能。在ImageNet 256×256数据集上,我们采用标准的隐空间生成协议,获得了1.54的1-NFE FID分数 ,在所有单步生成方法中达到了新的最优水平 。即便与多步的扩散模型或基于流匹配的模型相比,这一结果依然具备竞争力。此外,在更具挑战性的像素空间生成协议(即不使用隐空间)下,我们实现了1.61的1-NFE FID ,显著超越了以往的像素空间方法。这些结果表明,漂移模型为高质量、高效率的生成建模提供了一个富有前景的新范式。
2. Related Work
基于扩散/流的模型。 扩散模型(例如Sohl-Dickstein等人2015年;Ho等人2020年;Song等人2020年)及其基于流的对应模型(例如Lipman等人2022年;Liu等人2022年;Albergo等人2023年)通过微分方程(SDE或ODE)来形式化从噪声到数据的映射。其推理时计算的核心是迭代更新,例如采用欧拉求解器等形式:。其中更新量
依赖于神经网络 f,因此生成过程涉及多次网络评估。
已有大量研究工作致力于减少基于扩散/流的模型的生成步数。基于**蒸馏的方法**(例如Salimans & Ho 2022年;Luo等人2023年;Yin等人2024年;Zhou等人2024年)将预训练的多步模型蒸馏为单步模型。另一研究方向旨在**从头训练单步扩散/流模型**(例如Song等人2023年;Frans等人2024年;Boffi等人2025年;Geng等人2025a年)。为实现这一目标,这些方法通过近似诱导轨迹,将SDE/ODE动力学融入训练过程。相比之下,我们的工作提出了一种**概念上不同的新范式**,且不依赖于扩散/流模型所基于的SDE/ODE形式化框架。
**标准化流。**NFs(Rezende & Mohamed,2015;Dinh 等人,2016;Zhai 等人,2024)学习从数据到噪声的映射,并优化样本的对数似然。这些方法要求网络架构可逆且雅可比矩阵可计算。从概念上讲,NFs在推理时作为单步生成器运行,其计算通过网络的逆映射完成。
**矩匹配。**矩匹配方法(Dziugaite 等人,2015;Li 等人,2015)旨在最小化生成分布与数据分布之间的**最大均值差异**。近期,矩匹配已被扩展到单步/少步扩散模型中(Zhou 等人,2025)。与MMD相关,我们的方法也利用了核函数以及正负样本的概念。然而,我们的方法侧重于一个**漂移场**,该场显式地在训练时控制样本的漂移。更多讨论见附录C.2。
**对比学习。**我们的漂移场由来自数据分布的正样本和来自生成分布的负样本驱动。这在概念上与对比表示学习(Hadsell 等人,2006;Oord 等人,2018)中的正负样本相关。对比学习的思想也被扩展到生成模型中,例如应用于GANs(Unterthiner 等人,2017;Kang & Park,2020)或流匹配(Stoica 等人,2025)。
3. Drifting Models for Generation
我们提出漂移模型(Drifting Models),该模型将生成建模表述为通过漂移场对推前分布进行训练时的演化。我们的模型在推理时自然地执行一步生成。
3.1. Pushforward at Training Time


3.2. Drifting Field for Training


3.3. Designing the Drifting Field


公式解释



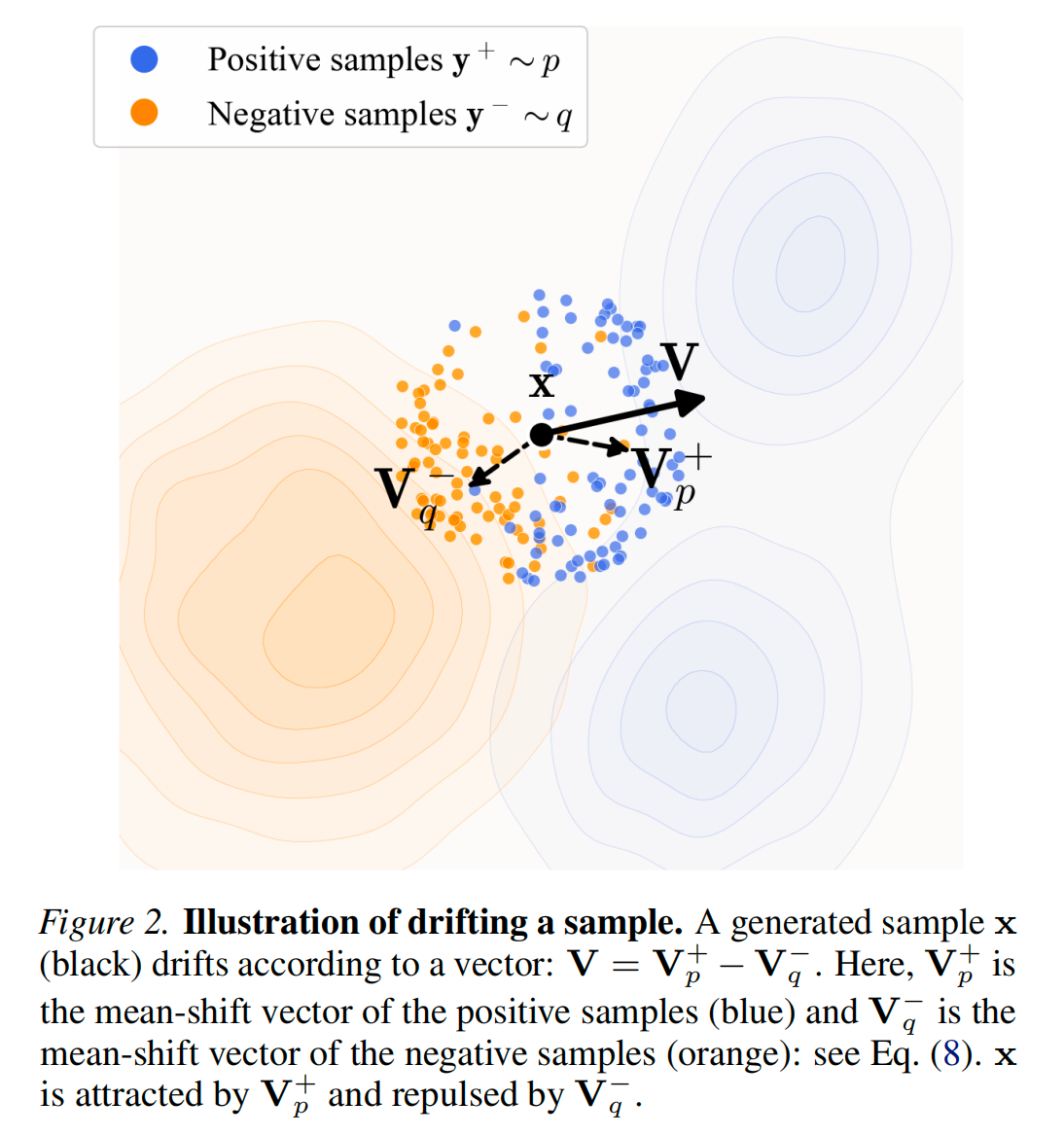
3.4. Drifting in Feature Space




3.5. Classifier-Free Guidance

4. Implementation for Image Generation
