CanMV K230 波形识别——数据分析（2）

说明

收集ADC采集到的数据，通过Python进行数据分析，采用DFT算法

1 准备工作

采集数据的csv文件
jupyter notebook/lab numpy matplotlib

2 导入数据

导入csv文件

python 复制代码

import numpy as np
FB = np.genfromtxt('***.csv', delimiter=',', dtype=float)  # 换成保存的变量名

例如，csv仅保留ADC数据列，代码如下

python 复制代码

Square = np.genfromtxt('Square.csv', delimiter=',', dtype=float)  
Triangular = np.genfromtxt('Triangular.csv', delimiter=',', dtype=float)  点数
Sine = np.genfromtxt('Sine.csv', delimiter=',', dtype=float)

绘制波形

python 复制代码

# 绘制波形 生成数据集
import matplotlib.pyplot as plt 
plt.subplot(3, 1, 1) 
plt.plot(Triangular[0:100])
plt.title('Triangular wave')    # 添加标题
plt.show()                      # 显示图形
plt.subplot(3, 1, 2) 
plt.plot(Square[0:100])
plt.title('Square wave')        # 添加标题
plt.show()                      # 显示图形
plt.subplot(3, 1, 3) 
plt.plot(Sine[0:100])
plt.title('Sine wave')          # 添加标题
plt.show()                      # 显示图形

输入结果如下

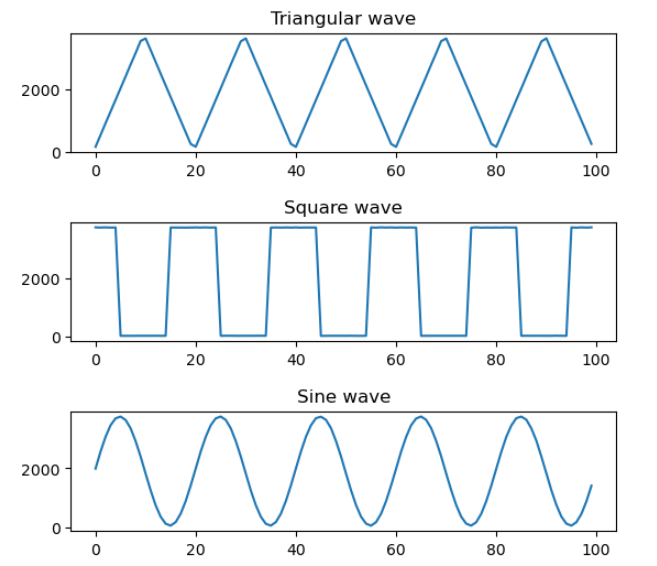
DFT处理

这里可以采用与MicroPython近似的定义

python 复制代码

import math
def DFT(x):
    Hw=[] # Hw H(w) 频域分布
    xl=len(x)
    for m in range(xl):
        ww=[]
        for n in range(xl):
            W=x[n]*np.exp(-1j*2*math.pi*n*m/xl)
            ww.append(W)
        Hw.append(sum(ww))
    Hw=np.array(Hw,dtype=np.complex64)
    return Hw
# 调用 DFT

调用DFT，绘制DFT结果

python 复制代码

# 绘制波形 生成数据集
# 计算实际幅值
Triangular_DFT=abs(DFT(Triangular[0:20]))*2/20
Square_DFT=abs(DFT(Square[0:20]))*2/20
Sine_DFT=abs(DFT(Sine[0:20]))*2/20
import matplotlib.pyplot as plt 
plt.subplot(3, 1, 1) 
plt.plot(Triangular_DFT)
plt.title('Triangular wave DFT')  # 添加标题
plt.show()                      # 显示图形
plt.subplot(3, 1, 2) 
plt.plot(Square_DFT)
plt.title('Square wave DFT')  # 添加标题
plt.show()                      # 显示图形
plt.subplot(3, 1, 3) 
plt.plot(Sine_DFT)
plt.title('Sine wave DFT')  # 添加标题
plt.show()                      # 显示图形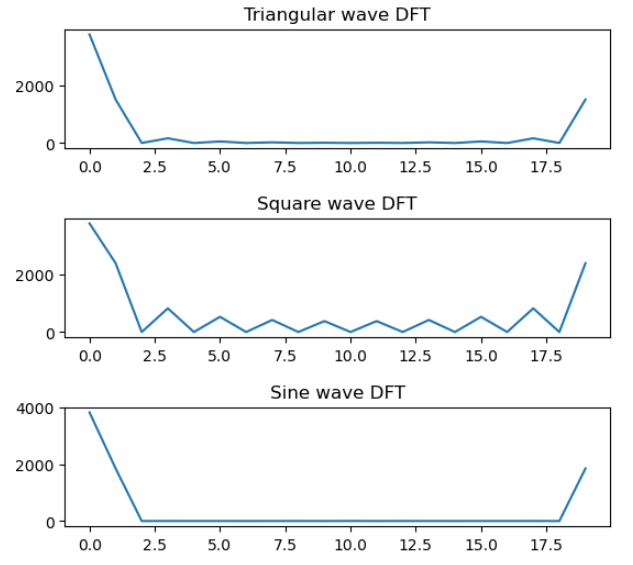

从DFT结果可以看出，除了第一个直流分量外，参数对称。

数据降维

原始信号长度为20 ，去除直流分量与幅值重复部分，取DFT $1-11$ 个参数，重新绘制如下

python 复制代码

# 绘制波形 特征数据
import matplotlib.pyplot as plt 
plt.subplot(3, 1, 1) 
plt.plot(Triangular_DFT[1:11])
plt.title('Triangular wave DFT')  # 添加标题
plt.show()                      # 显示图形
plt.subplot(3, 1, 2) 
plt.plot(Square_DFT[1:11])
plt.title('Square wave DFT')  # 添加标题
plt.show()                      # 显示图形
plt.subplot(3, 1, 3) 
plt.plot(Sine_DFT[1:11])
plt.title('Sine wave DFT')  # 添加标题
plt.show()                      # 显示图形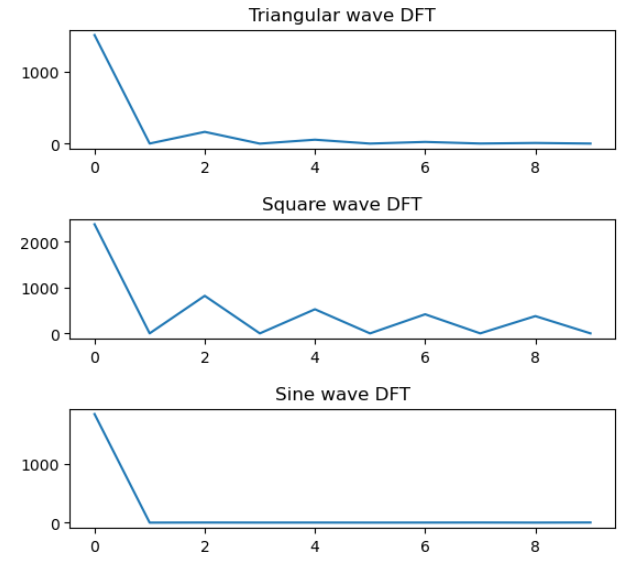

从DFT结果可以看出，频谱的幅值存在差异，后续设计分类器进行识别