核心定义
标准差 是衡量一组数据离散程度 或波动大小的最常用、最重要的指标。它描述的是数据点相对于其平均值的平均偏离距离。
简单来说:
-
标准差小 → 数据点紧密围绕在平均值周围,波动小,更稳定。
-
标准差大 → 数据点分散得离平均值远,波动大,变异性强。
为什么需要标准差?(与平均值的对比)
平均值告诉我们数据的"中心"在哪里,但它掩盖了数据的分布情况。
例如:两个班级的数学平均分都是75分。
-
A班分数:
[74, 75, 76, 75, 75]→ 非常集中。 -
B班分数:
[90, 60, 100, 50, 55]→ 非常分散。
它们的平均值相同 ,但离散程度天差地别。标准差就是用来量化这种"离散程度"的。
计算公式与符号
-
总体标准差:当你的数据是整个研究群体时使用。
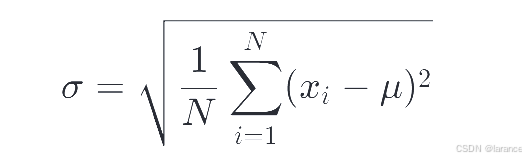
-
σ:总体标准差(读作"西格玛")
-
N:总体中数据的个数
-
xix:每个数据点
-
μ:总体平均值
-
样本标准差:当你的数据只是从总体中抽取的一个样本时使用(更常见)。
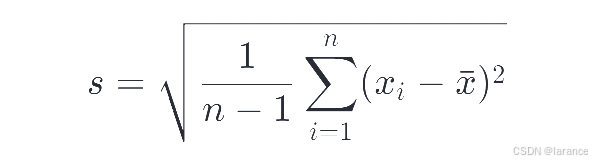
-
s:样本标准差
-
n:样本中数据的个数
-
xˉ:样本平均值
-
关键区别 :分母是 n−1 而不是 n,这称为"贝塞尔校正",目的是用样本标准差来无偏估计总体标准差。
-
计算步骤(以样本标准差为例):
-
计算样本平均值 xˉ。
-
计算每个数据点与平均值的差:xi−xˉ。
-
将每个差值平方:(xi−xˉ)2为了消除负号并放大较大偏差)。
-
求这些平方差的和:∑(xi−xˉ)2∑(xi−xˉ)2。
-
除以 n−1,得到方差 s2s2。
-
对方差 开平方根,即得到标准差 s。
关键点与解释
-
单位 :标准差的单位和原始数据的单位相同(因为方差开了平方根),这使其比方差更易于解释。
-
经验法则(正态分布) :
对于一个近似正态分布的数据集:
-
约68%的数据落在均值 ±1 个标准差范围内。
-
约95%的数据落在均值 ±2 个标准差范围内。
-
约99.7%的数据落在均值 ±3 个标准差范围内
-