1. 适合场景
单调栈适合解决 ------ 求当前元素左边或者右边,第一个比当前元素大或者小的元素,找到这个元素,就可以找到这个数值或者下标,再做相关的计算。
2. 作用
单调栈的作用 ------ 存放遍历过后的元素,这样可以和当前遍历元素做一个对比。
3. 特性
具有单调性,要么单调递增,要么单调递减,通过当前元素与栈顶元素作比较,决定是否放入栈中,实现单调递减/单调递增。
相关题目:
题目:向左看齐(单调递减)
cpp描述 给定一个长度为n的数组a 1,a[2],....,a[n],输出每个位置i上,左边最近的小于a[i]的位置,如果不存在则输出0。 如n=4时 a = {4,7,6,10} 应该按顺序输出0 1 1 3 解释: i=1时,4左边没有比它小的,输出0 i=2时,7左侧最近比它小的,在下标为1的位置 i=3时,6左侧最近比它小的,在下标为1的位置 i=4时,10左侧最近比它小的,在下标为3的位置 输入描述 第一行一个整数n,代表元素个数,n<=1e5 第二行n个数,代表每个a[i],空格隔开, a[i]<=1e9 输出描述 n个数l[1],l[2],...l[n],每个l[i]代表在原数组第i个位置上,左侧最近的小于a[i]的位置。 用例输入 1 4 4 7 6 10 用例输出 1 0 1 1 3代码:
cpp#include<bits/stdc++.h> using namespace std; int n,a[100005]; int main(){ cin>>n; a[0]=0; stack<int> s; for(int i=1;i<=n;i++){ cin>>a[i]; while(s.size() && a[s.top()]>=a[i]){ s.pop(); } if(s.size())cout<<s.top()<<' '; else cout<<0<<' '; s.push(i); } return 0; }
题目:洛谷 P5788【模板】单调栈(单调递增)
cpp# P5788 【模板】单调栈 ## 题目背景 模板题,无背景。 2019.12.12 更新数据,放宽时限,现在不再卡常了。 ## 题目描述 给出项数为 n 的整数数列 a_{1 dots n}。 定义函数 f(i) 代表数列中第 i 个元素之后第一个大于 a[i] 的元素的**下标**,即 f(i)=min_{i<j<=q n, a[j] > a[i]} {j}。若不存在,则 f(i)=0。 试求出 f(1dots n)。 ## 输入格式 第一行一个正整数 n。 第二行 n 个正整数 a[1]...a[n]。 ## 输出格式 一行 n 个整数表示 f(1), f(2) ...... f(n) 的值。 ## 输入输出样例 #1 ### 输入 #1 ``` 5 1 4 2 3 5 ``` ### 输出 #1 ``` 2 5 4 5 0 ``` ## 说明/提示 【数据规模与约定】 对于 30% 的数据,n<=100; 对于 60% 的数据,n<=5*10^3 ; 对于 100% 的数据,1<=n<=3*10^6,1<=a[i]<=10^9。代码:
cpp#include<bits/stdc++.h> using namespace std; const int MAXN=3e6+10; int a[MAXN],ans[MAXN]; int main(){ int n; cin>>n; for(int i=1;i<=n;i++)cin>>a[i]; stack<int> s; for(int i=n;i>=1;i--){ while(s.size() && a[s.top()]<=a[i]) s.pop(); ans[i]=!s.size()?0:s.top(); s.push(i); } for(int i=1;i<=n;i++)cout<<ans[i]<<" "; return 0; } //和上一个题目单调递减仅需更改循环从从小到大变成从大到小, //while里面的判断循环条件栈顶从>=变成<=
题目:Aki的能量防护墙(需要同时进行单调递增和单调递减求最大值)
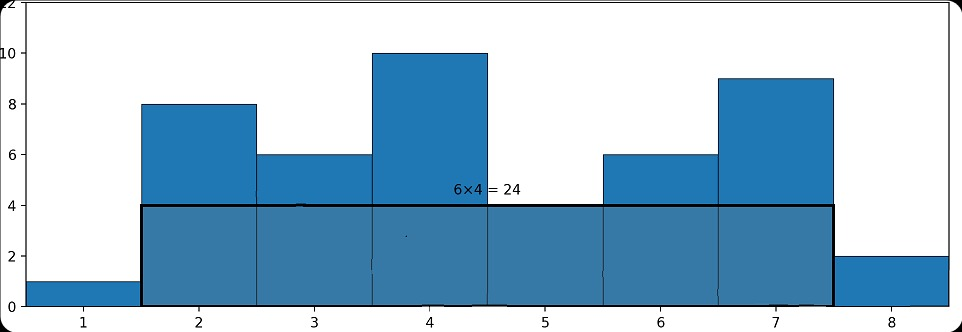
cpp描述 在"方块城"的主干道上,工程师Aki正在搭建一排 能量防护墙模块。 第 i 个模块的 宽度恒为 1,高度为 h i 。所有模块底部都在同一条水平基线上。 Aki想从这排模块中选出一段 连续 的模块,把它们拼成一个矩形防护墙。 很显然,一个有效的矩形防护墙的高度取决于拼成它的矩形中的最小高度。 你的任务是:求能拼出的 最大矩形防护墙面积(面积 = 高度 × 宽度)。 例如: 8 1 8 6 10 4 6 9 2 会选择第2个到第7个模块组成矩形防护墙,此时组成的面积最大,为6x4=24。 输入描述 第一行输入一个整数 n,表示模块数量。 1 ≤ n ≤ 100000 第二行输入 n 个整数 h1 ... hn,表示每个模块高度: 0 ≤ hi ≤ 1000000000 每个模块宽度均为 1。 输出描述 输出一行一个整数,表示最大矩形面积。 用例输入 1 8 1 8 6 10 4 6 9 2 用例输出 1 24
代码:
cpp#include<bits/stdc++.h> using namespace std; const int N=1e5+10; long long a[N],n,r[N],l[N],sum; int main(){ cin>>n; for(int i=1;i<=n;i++)cin>>a[i]; stack<int> s; for(int i=n;i>=1;i--){ while(s.size() && a[s.top()]>=a[i])s.pop(); r[i]=!s.size()?n+1:s.top(); s.push(i); } while(s.size())s.pop(); for(int i=1;i<=n;i++){ while(s.size() && a[s.top()]>=a[i])s.pop(); l[i]=!s.size()?0:s.top(); s.push(i); } for(int i=1;i<=n;i++){ sum=max(sum,a[i]*(r[i]-l[i]-1)); } cout<<sum; return 0; }
题目:洛谷 P2422 良好的感觉(结合单调栈(和上一个题目相同,都需要递增和递减,代码几乎不用变,还要加上一个前缀和求区间和)
cpp# P2422 良好的感觉 ## 题目描述 kkk 做了一个人体感觉分析器。每一天,人都有一个感受值A[i],A[i] 越大,表示人感觉越舒适。在一段时间[i,j]内,人的舒适程度定义为left[i,j]中最不舒服的那一天的感受值*[i,j]中每一天感受值的和。现在给出 kkk 在连续 N 天中的感受值,请问,在哪一段时间,kkk 感觉最舒适? ## 输入格式 第一行为 N,代表数据记录的天数。 第二行 N 个整数,代表每一天的感受值。 ## 输出格式 一行,表示在最舒适的一段时间中的感受值。 ## 输入输出样例 #1 ### 输入 #1 ``` 6 3 1 6 4 5 2 ``` ### 输出 #1 ``` 60 ``` ## 说明/提示 kkk 最开心的一段时间是第 3 天到第 5 天,开心值:$(6+4+5)*4=60。 对于 30% 的数据,1<=N<=100。 对于 70% 的数据,1<=N<=2000。 对于 100% 的数据,1<=N<=10^5,1<=感受值<=10^6。代码:
cpp#include<bits/stdc++.h> using namespace std; const int N=1e5+10; long long a[N],n,r[N],l[N],sum,num[N]; int main(){ cin>>n; for(int i=1;i<=n;i++)cin>>a[i]; stack<int> s; for(int i=n;i>=1;i--){ while(s.size() && a[s.top()]>=a[i])s.pop(); r[i]=!s.size()?n+1:s.top(); s.push(i); } while(s.size())s.pop(); for(int i=1;i<=n;i++){ while(s.size() && a[s.top()]>=a[i])s.pop(); l[i]=!s.size()?0:s.top(); s.push(i); } /* a 1 2 3 4 num 1 3 6 10 */ // [2,3] num[3] - num[1] num[0]=0; for(int i=1;i<=n;i++){ num[i]=a[i]+num[i-1]; } for(int i=1;i<=n;i++){ sum=max(sum,a[i]*(num[r[i]-1]-num[l[i]])); } cout<<sum; return 0; }
题目:洛谷 P2947 [USACO09MAR] Look Up S(单调递增 )
cpp# P2947 [USACO09MAR] Look Up S ## 题目描述 约翰的 N(1<=N<=10^5) 头奶牛站成一排,奶牛 i 的身高是 H[i](1<=H[i]<=10^6)。现在,每只奶牛都在向右看。对于奶牛 i,如果奶牛 j 满足 i<j 且 H[i]<H[j],我们可以说奶牛 i 可以仰望奶牛 j。 求出每只奶牛离她最近的仰望对象。 ## 输入格式 第 1 行输入 N,之后 N 行第 i+1 行输入一个身高 H_i。 ## 输出格式 共 N 行,按顺序每行输出一只奶牛的最近仰望对象,如果没有仰望对象,输出 0。 ## 输入输出样例 #1 ### 输入 #1 ``` 6 3 2 6 1 1 2 ``` ### 输出 #1 ``` 3 3 0 6 6 0 ``` ## 说明/提示 **【输入说明】** 6 头奶牛的身高分别为 3, 2, 6, 1, 1, 2。 **【输出说明】** 奶牛 1,2 仰望奶牛 3,奶牛 4,5 仰望奶牛 6,奶牛 3 和 6 没有仰望对象。 **【数据规模】** 对于 20% 的数据:1<=N<=10; 对于 50% 的数据:1<=N<=10^3; 对于 100% 的数据:1<=N<=10^5,1<=H_i<=10^6。代码:
cpp#include<bits/stdc++.h> using namespace std; const int N=1e5+10; int n,a[N],ans[N]; int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; } stack<int> s; for(int i=n;i>=1;i--){ while(s.size() && a[s.top()]<=a[i]) s.pop(); ans[i]=!s.size()?0:s.top(); s.push(i); } for(int i=1;i<=n;i++)cout<<ans[i]<<endl; return 0; }