本文参考Pozar的微波工程。仅供学习使用
2.3 端接负载的无耗传输线
图2.4端接负载阻抗的传输线
图 2.4 画出了一个端接任意负载阻抗 ZLZ_{L}ZL 的无耗传输线。这个问题将说明传输线中的波反射,这是分布系统的一个基本特性。这里设向右为Z正方向,负载接在Z=0处
反射波产生由来,特性阻抗负载阻抗失配导致不满足同一个电压电流关系。
假定有形式为 Vo+e−jβzV_{o}^{+} e^{-j \beta z}Vo+e−jβz 的入射波,它产生于 z<0z < 0z<0 处的源。我们已经知道,这一行波的电压和电流之比就是特征阻抗 Z0Z_{0}Z0。但是,当该传输线端接任意负载 ZL≠Z0Z_{L} \neq Z_{0}ZL=Z0 时,负载上的电压和电流之比应是 ZLZ_{L}ZL。
因此,要满足这个条件,必定会产生具有适当振幅的反射波。传输线上的总电压可以作为入射波与反射波之和写成2.1节中式(2.14a)的形式:
V(z)=Vo+e−jβz+Vo−ejβz(2.34a) V(z)=V_{o}^{+} e^{-j \beta z}+V_{o}^{-} e^{j \beta z} \quad (2.34 \text{a}) V(z)=Vo+e−jβz+Vo−ejβz(2.34a)
类似地,传输线上的总电流可以由式(2.14b)描述:
I(z)=Vo+Z0e−jβz−Vo−Z0ejβz(2.34b) I(z)=\frac{V_{o}^{+}}{Z_{0}} e^{-j \beta z}-\frac{V_{o}^{-}}{Z_{0}} e^{j \beta z} \quad (2.34 \text{b}) I(z)=Z0Vo+e−jβz−Z0Vo−ejβz(2.34b)
我们想要将上述俩方程用入射波Vo+V_{o}^{+}Vo+表示。
利用边界条件:负载总电压和总电流通过ZLZ_{L}ZL联系起来,因此在 z=0z = 0z=0 处必定有
ZL=V(0)I(0)=Vo++Vo−Vo+−Vo−Z0 Z_{L}=\frac{V(0)}{I(0)}=\frac{V_{o}^{+}+V_{o}^{-}}{V_{o}^{+}-V_{o}^{-}} Z_{0} ZL=I(0)V(0)=Vo+−Vo−Vo++Vo−Z0
求得 Vo−V_{o}^{-}Vo− 为
Vo−=ZL−Z0ZL+Z0Vo+ V_{o}^{-}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}} V_{o}^{+} Vo−=ZL+Z0ZL−Z0Vo+
这本表达式将反射波用入射波表示,定义电压反射系数 Γ\GammaΓ:Vo−=ΓVo+V_{o}^{-}=\Gamma V_{o}^{+}Vo−=ΓVo+
Γ=Vo−Vo+=ZL−Z0ZL+Z0(2.35) \Gamma=\frac{V_{o}^{-}}{V_{o}^{+}}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}} \quad{(2.35)} Γ=Vo+Vo−=ZL+Z0ZL−Z0(2.35)
利用电压反射系数 Γ\GammaΓ消去反射波传输线上的总电压和总电流可以写为
V(z)=Vo+(e−jβz+Γejβz)(2.36a) V(z)=V_{o}^{+}\left(e^{-j \beta z}+\Gamma e^{j \beta z}\right) \quad{(2.36a)} V(z)=Vo+(e−jβz+Γejβz)(2.36a)
I(z)=Vo+Z0(e−jβz−Γejβz)(2.36b) I(z)=\frac{V_{o}^{+}}{Z_{0}}\left(e^{-j \beta z}-\Gamma e^{j \beta z}\right) \quad{(2.36b)} I(z)=Z0Vo+(e−jβz−Γejβz)(2.36b)
从这些表达式可以看出,线上的电压和电流是入射波和反射波的叠加;这样的波称为驻波。只有当 Γ=0\Gamma=0Γ=0 时,才不会有反射波。为了得到 Γ=0\Gamma=0Γ=0,负载阻抗 ZLZ_{L}ZL 必须等于该传输线的特征阻抗 Z0Z_{0}Z0,这可以由式(2.35)看出。因为入射波没有反射,这样的负载称为传输线的匹配负载。
现在考虑传输线上 zzz 点的时间平均功率流:
Pavg=12Re{V(z)I(z)∗}=12∣Vo+∣2Z0Re{1−Γ∗e−2jβz+Γe2jβz−∣Γ∣2} P_{\text{avg}}=\frac{1}{2} \operatorname{Re}\left\{V(z) I(z)^{*}\right\}=\frac{1}{2} \frac{\left|V_{o}^{+}\right|^{2}}{Z_{0}} \operatorname{Re}\left\{1-\Gamma^{*} e^{-2 j \beta z}+\Gamma e^{2 j \beta z}-|\Gamma|^{2}\right\} Pavg=21Re{V(z)I(z)∗}=21Z0∣Vo+∣2Re{1−Γ∗e−2jβz+Γe2jβz−∣Γ∣2}
上式中应用了式(2.36)。括号中的中间两项有形式 A−A∗=2jIm(A)A-A^{*}=2 j \operatorname{Im}(A)A−A∗=2jIm(A),是纯虚数,因此可以简化为
Pavg=12∣Vo+∣2Z0(1−∣Γ∣2)(2.37) P_{\text{avg}}=\frac{1}{2} \frac{\left|V_{o}^{+}\right|^{2}}{Z_{0}}\left(1-|\Gamma|^{2}\right) \quad{(2.37)} Pavg=21Z0∣Vo+∣2(1−∣Γ∣2)(2.37)
这表明线上任意一点的平均功率流是常数,而且传送到负载的总功率流(PavgP_{avg}Pavg)等于入射功率(∣Vo+∣2/2Z0\left|V_{o}^{+}\right|^{2}/2Z_{0}∣Vo+∣2/2Z0)减去反射功率(∣Vo∣2∣Γ∣2/2Z0\left|V_{o}\right|^{2}\left|\Gamma\right|^{2}/2Z_{0}∣Vo∣2∣Γ∣2/2Z0)。若 Γ=0\Gamma=0Γ=0,则传送到负载的功率最大;若 Γ=1\Gamma=1Γ=1,则没有功率到达负载。上述讨论假定源是匹配的,因而没有来自 z<0z<0z<0 的区域的反射波的再反射。
当负载失配时,不是所有来自源的可用功率都传给了负载。这种"损耗"称为回波损耗(Return Loss, RL),它定义(以dB为单位)为
RL=−20lg∣Γ∣ dB(2.38) RL=-20\lg|\Gamma| \text{ dB} \qquad (2.38) RL=−20lg∣Γ∣ dB(2.38)
因此,匹配负载(Γ=0\Gamma=0Γ=0)具有 ∞\infty∞ dB的回波损耗(无反射功率),而全反射(∣Γ∣=1|\Gamma|=1∣Γ∣=1)具有0 dB的回波损耗(所有的入射功率都被反射回来)。
若负载与线是匹配的,则 Γ=0\Gamma=0Γ=0,而且线上的电压幅值 ∣V(z)∣=∣Vo+∣\left|V(z)\right|=\left|V_{o}^{+}\right|∣V(z)∣=∣Vo+∣ 为常数。这样的传输线有时称为是平坦的(幅度是恒定的,不随测量位置z的变化而变化 )。然而,当负载失配时,反射波的存在会导致驻波,这时线上的电压幅值不是常数。因此,由式(2.36a)提取公因子e−jβze^{-j\beta z}e−jβz:
V(z)=Vo+e−jβz(1+Γejβz/e−jβz)V(z)=Vo+e−jβz(1+Γej2βz) V(z) = V_o^+ e^{-j\beta z} (1 + \Gamma e^{j\beta z} / e^{-j\beta z}) V(z) = V_o^+ e^{-j\beta z} (1 + \Gamma e^{j2\beta z}) V(z)=Vo+e−jβz(1+Γejβz/e−jβz)V(z)=Vo+e−jβz(1+Γej2βz)
电压的幅度 ∣V(z)∣|V(z)|∣V(z)∣ 是其复模。根据复数模的性质∣A⋅B∣=∣A∣⋅∣B∣|A \cdot B| = |A| \cdot |B|∣A⋅B∣=∣A∣⋅∣B∣,有:
∣V(z)∣=∣Vo+∣⋅∣e−jβz∣⋅∣1+Γej2βz∣ |V(z)| = |V_o^+| \cdot |e^{-j\beta z}| \cdot |1 + \Gamma e^{j2\beta z}| ∣V(z)∣=∣Vo+∣⋅∣e−jβz∣⋅∣1+Γej2βz∣
对任意实数θ\thetaθ,有∣ejθ∣=1|e^{j\theta}| = 1∣ejθ∣=1,所以 ∣e−jβz∣=1|e^{-j\beta z}| = 1∣e−jβz∣=1。因此:
∣V(z)∣=∣Vo+∣⋅∣1+Γej2βz∣ |V(z)| = |V_o^+| \cdot |1 + \Gamma e^{j2\beta z}| ∣V(z)∣=∣Vo+∣⋅∣1+Γej2βz∣
从负载端看向源方向 的距离定义设为ℓ\ellℓ:
ℓ=−z \ell = -z ℓ=−z
将z=−ℓz = -\ellz=−ℓ代入幅度公式:
∣V(z)∣=∣Vo+∣⋅∣1+Γe−j2βℓ∣ |V(z)| = |V_o^+| \cdot |1 + \Gamma e^{-j2\beta \ell}| \quad \ ∣V(z)∣=∣Vo+∣⋅∣1+Γe−j2βℓ∣
反射系数 Γ\GammaΓ是一个复数,描述了反射波的幅度和相位相对于入射波的变化。我们将其写为极坐标形式:
Γ=∣Γ∣ejθ \Gamma = |\Gamma| e^{j\theta} Γ=∣Γ∣ejθ
其中:
∣Γ∣|\Gamma|∣Γ∣是反射系数的幅度 (0≤∣Γ∣≤10 \leq |\Gamma| \leq 10≤∣Γ∣≤1)。
θ\thetaθ是反射系数的相位角 (通常在负载处z=0z=0z=0或ℓ=0\ell=0ℓ=0定义)。
将Γ=∣Γ∣ejθ\Gamma = |\Gamma| e^{j\theta}Γ=∣Γ∣ejθ代入上一步的公式:
∣V(z)∣=∣Vo+∣⋅∣1+∣Γ∣ejθ⋅e−j2βℓ∣ |V(z)| = |V_o^+| \cdot |1 + |\Gamma| e^{j\theta} \cdot e^{-j2\beta \ell}| ∣V(z)∣=∣Vo+∣⋅∣1+∣Γ∣ejθ⋅e−j2βℓ∣
将指数项合并:
∣V(z)∣=∣Vo+∣⋅∣1+∣Γ∣ej(θ−2βℓ)∣(2.39) |V(z)| = |V_o^+| \cdot |1 + |\Gamma| e^{j(\theta - 2\beta \ell)}| \quad (2.39) ∣V(z)∣=∣Vo+∣⋅∣1+∣Γ∣ej(θ−2βℓ)∣(2.39)
式中,ℓ=−z\ell=-zℓ=−z 是从 z=0z=0z=0 的负载处开始测量的正距离,θ\thetaθ 是反射系数的相位(Γ=∣Γ∣ejθ\Gamma=|\Gamma|e^{j\theta}Γ=∣Γ∣ejθ只取决于负载和特性阻抗)。这个结果表明,电压幅值沿传输线随 zzz 起伏。当相位项 ej(θ−2βℓ)=1e^{j(\theta-2\beta\ell)}=1ej(θ−2βℓ)=1 时出现最大值如下式:
Vmax=∣Vo+∣(1+∣Γ∣)(2.40a) V_{\text{max}}=|V_{o}^{+}|(1+|\Gamma|) \qquad (2.40a) Vmax=∣Vo+∣(1+∣Γ∣)(2.40a)
给出。当相位项 ej(θ−2βℓ)=−1e^{j(\theta-2\beta\ell)}=-1ej(θ−2βℓ)=−1 时出现最小值如下式:
Vmin=∣Vo+∣(1−∣Γ∣)(2.40b) V_{\text{min}}=|V_{o}^{+}|(1-|\Gamma|) \qquad (2.40b) Vmin=∣Vo+∣(1−∣Γ∣)(2.40b)
给出。**当 ∣Γ∣|\Gamma|∣Γ∣ 增加时,VmaxV_{\max}Vmax 与 VminV_{\min}Vmin即最大最小电压之比增加,因此度量传输线的失配量,**称为驻波比(Standing Wave Ratio, SWR),可以定义为
SWR=VmaxVmin=1+∣Γ∣1−∣Γ∣(2.41) S W R=\frac{V_{\max }}{V_{\min }}=\frac{1+|\Gamma|}{1-|\Gamma|} \qquad (2.41) SWR=VminVmax=1−∣Γ∣1+∣Γ∣(2.41)
这个量也称电压驻波比(Voltage Standing Wave Ratio, VSWR)。由式(2.41)可以看出,SWR是一个实数,且 1⩽SWR⩽∞1\leqslant S W R\leqslant\infty1⩽SWR⩽∞,其中 SWR=1S W R=1SWR=1 意味着反射系数为零负载匹配。
λ=2πβ=2πωLC(2.15) \lambda = \frac{2\pi}{\beta} = \frac{2\pi}{\omega \sqrt{LC}} \quad (2.15) λ=β2π=ωLC 2π(2.15)
∣V(z)∣=∣Vo+∣⋅∣1+∣Γ∣ej(θ−2βℓ)∣(2.39) |V(z)| = |V_o^+| \cdot |1 + |\Gamma| e^{j(\theta - 2\beta \ell)}| \quad (2.39) ∣V(z)∣=∣Vo+∣⋅∣1+∣Γ∣ej(θ−2βℓ)∣(2.39)
由式(2.39)看出,两个连续电压最大值(或最小值)之间的距离是 ℓ=2π/(2β)=πλ/2π=λ/2\ell=2\pi /(2\beta)=\pi\lambda /2\pi=\lambda/2ℓ=2π/(2β)=πλ/2π=λ/2,而最大值和相邻最小值之间的距离是 ℓ=π/(2β)=λ/4\ell=\pi /(2\beta)=\lambda/4ℓ=π/(2β)=λ/4,其中 λ\lambdaλ 是传输线上的波长。
反射系数式(2.35)定义为负载处(ℓ=0\ell=0ℓ=0)反射波与入射波电压的振幅之比,但这个量也可以像下面那样推广为线上任意点 ℓ\ellℓ 处的值。由式(2.34a),当 z=−ℓz=-\ellz=−ℓ 时,反射分量与入射分量之比为
Γ=Vo−Vo+=ZL−Z0ZL+Z0=Γ(0)(2.35)ℓ=0处 \Gamma=\frac{V_{o}^{-}}{V_{o}^{+}}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=\Gamma(0) \quad{(2.35)\ell=0处} Γ=Vo+Vo−=ZL+Z0ZL−Z0=Γ(0)(2.35)ℓ=0处
Γ(ℓ)=Vo−e−jβℓVo+ejβℓ=Γ(0)e−2jβℓ(2.42) \Gamma(\ell)=\frac{V_{o}^{-} e^{-j\beta\ell}}{V_{o}^{+} e^{j\beta\ell}}=\Gamma(0) e^{-2j\beta\ell} \qquad (2.42) Γ(ℓ)=Vo+ejβℓVo−e−jβℓ=Γ(0)e−2jβℓ(2.42)
式中,Γ(0)\Gamma(0)Γ(0) 是 z=0z=0z=0 处的反射系数。当需要将负载的失配效应变换到传输线上时,这种形式是有用的。
我们已经看到,线上的实功率流是常数,但电压的振幅,至少对失配的传输线而言,是随线上的位置而起伏的。因此,读者可能会得出结论:从线上看到的阻抗必定随位置变化。事实的确如此。在距离负载 ℓ=−z\ell=-zℓ=−z 处,向负载看去的输入阻抗是
Zin =V(−ℓ)I(−ℓ)=Vo+(ejβℓ+Γe−jβℓ)Vo+(ejβℓ−Γe−jβℓ)Z0=1+Γe−2jβℓ1−Γe−2jβℓZ0(2.43) Z_{\text {in }}=\frac{V(-\ell)}{I(-\ell)}=\frac{V_{o}^{+}\left(e^{j \beta \ell}+\Gamma e^{-j \beta \ell}\right)}{V_{o}^{+}\left(e^{j \beta \ell}-\Gamma e^{-j \beta \ell}\right)} Z_{0}=\frac{1+\Gamma e^{-2 j \beta \ell}}{1-\Gamma e^{-2 j \beta \ell}} Z_{0} \qquad (2.43) Zin =I(−ℓ)V(−ℓ)=Vo+(ejβℓ−Γe−jβℓ)Vo+(ejβℓ+Γe−jβℓ)Z0=1−Γe−2jβℓ1+Γe−2jβℓZ0(2.43)
式中,V(z)V(z)V(z) 和 I(z)I(z)I(z) 已经用到了式(2.36a, b)。一个更有用的形式可以通过在式(2.43)中应用 Γ\GammaΓ 的表达式(2.35)得到:
Zin =Z0(ZL+Z0)ejβℓ+(ZL−Z0)e−jβℓ(ZL+Z0)ejβℓ−(ZL−Z0)e−jβℓ Z_{\text {in }}=Z_{0} \frac{\left(Z_{L}+Z_{0}\right) \mathrm{e}^{\mathrm{j} \beta \ell}+\left(Z_{L}-Z_{0}\right) \mathrm{e}^{-\mathrm{j} \beta \ell}}{\left(Z_{L}+Z_{0}\right) \mathrm{e}^{\mathrm{j} \beta \ell}-\left(Z_{L}-Z_{0}\right) \mathrm{e}^{-\mathrm{j} \beta \ell}} Zin =Z0(ZL+Z0)ejβℓ−(ZL−Z0)e−jβℓ(ZL+Z0)ejβℓ+(ZL−Z0)e−jβℓ
=Z0ZLcosβℓ+jZ0sinβℓZ0cosβℓ+jZLsinβℓ =Z_{0} \frac{Z_{L} \cos \beta \ell+\mathrm{j} Z_{0} \sin \beta \ell}{Z_{0} \cos \beta \ell+\mathrm{j} Z_{L} \sin \beta \ell} =Z0Z0cosβℓ+jZLsinβℓZLcosβℓ+jZ0sinβℓ
=Z0ZL+jZ0tanβℓZ0+jZLtanβℓ(2.44) =Z_{0} \frac{Z_{L}+\mathrm{j} Z_{0} \tan \beta \ell}{Z_{0}+\mathrm{j} Z_{L} \tan \beta \ell}\quad (2.44) =Z0Z0+jZLtanβℓZL+jZ0tanβℓ(2.44)
这是一个重要的结果,它给出了具有任意负载阻抗的一段传输线在任何位置处看到的的输入阻抗,我们把这一结果称为传输线阻抗方程,。下面将考虑一些特殊情况。
2.3.1 无耗传输线的特殊情况
在工作中,我们经常遇到一些无耗传输线的特殊情况,因此这里有必要考虑这些情况的特性。
SWR=VmaxVmin=1+∣Γ∣1−∣Γ∣(2.41) S W R=\frac{V_{\max }}{V_{\min }}=\frac{1+|\Gamma|}{1-|\Gamma|} \qquad (2.41) SWR=VminVmax=1−∣Γ∣1+∣Γ∣(2.41)
图2.5 终端短路的传输线
首先考虑图2.5所示的传输线电路,其中传输线的一端是短路的,即 ZL=0Z_{L}=0ZL=0。由式(2.35)可以看出,短路负载的反射系数是 Γ=−1\Gamma=-1Γ=−1;然后,由式(2.41)得知驻波比为无穷大。由式(2.36)得出传输线上的电压和电流为
V(z)=Vo+(e−jβz−ejβz)=−2jVo+sinβz(2.45a) V(z)=V_{o}^{+}\left(\mathrm{e}^{-\mathrm{j} \beta z}-\mathrm{e}^{\mathrm{j} \beta z}\right)=-2 \mathrm{j} V_{o}^{+} \sin \beta z \qquad (2.45a) V(z)=Vo+(e−jβz−ejβz)=−2jVo+sinβz(2.45a)
I(z)=Vo+Z0(e−jβz+ejβz)=2Vo+Z0cosβz(2.45b) I(z)=\frac{V_{o}^{+}}{Z_{0}}\left(\mathrm{e}^{-\mathrm{j} \beta z}+\mathrm{e}^{\mathrm{j} \beta z}\right)=\frac{2 V_{o}^{+}}{Z_{0}} \cos \beta z \qquad (2.45b) I(z)=Z0Vo+(e−jβz+ejβz)=Z02Vo+cosβz(2.45b)
它表明,在负载处,V=0V=0V=0(对于短路负载,这是预料之中的),而电流是极大值。由式(2.44)或比值 V(−ℓ)/I(−ℓ)V(-\ell)/I(-\ell)V(−ℓ)/I(−ℓ),得出输入阻抗为
Zin =Z0jZ0sinβℓZ0cosβℓ=jZ0tanβℓ(2.45c) Z_{\text {in }}=Z_{0} \frac{\mathrm{j} Z_{0} \sin \beta \ell}{Z_{0} \cos \beta \ell}=j Z_{0} \tan \beta \ell \qquad (2.45c) Zin =Z0Z0cosβℓjZ0sinβℓ=jZ0tanβℓ(2.45c)
可以看到,对任意长度 lll,它都是纯虚数,而且可取 +j∞+j\infty+j∞ 到 −j∞-j\infty−j∞ 之间的所有值。例如,当 l=0l=0l=0 时,有 Zin=0Z_{\text {in}}=0Zin=0,但当 l=λ/4l=\lambda/4l=λ/4 时有 Zin=∞Z_{\text {in}}=\inftyZin=∞(开路)。式(2.45c)还表明,阻抗是 lll 的周期函数,对 l/2l/2l/2 的整数倍重复。短路传输线的电压、电流和输入阻抗已绘于图2.6中。
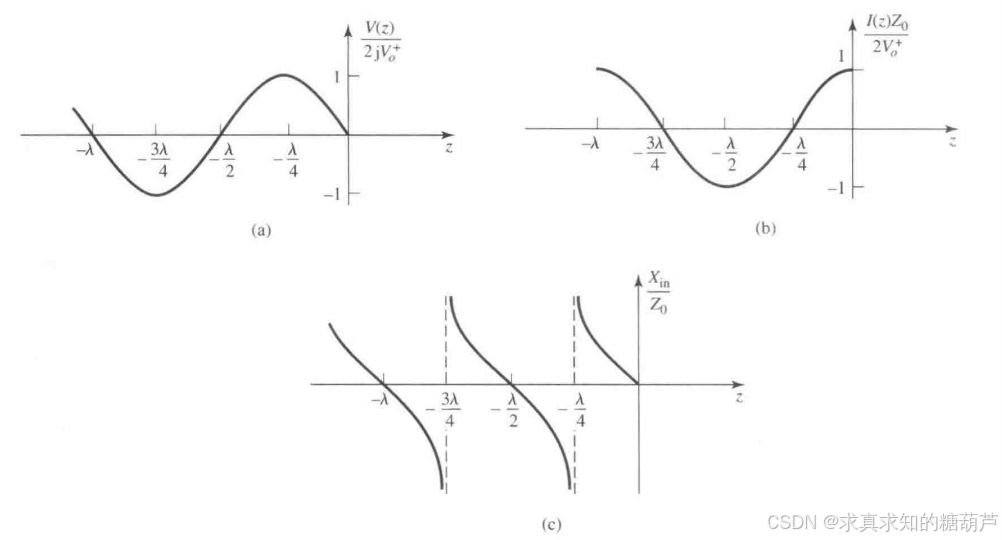
图2.6 (a)电压、(b)电流和©阻抗(Rin=0R_{in}=0Rin=0 或 ∞\infty∞)沿短路传输线的变化
下面考虑图2.7所示的开路线,其中 ZL=∞Z_{L}=\inftyZL=∞。将式(2.35)的分子和分母除以 ZLZ_{L}ZL 并令 ZL→∞Z_{L}\to\inftyZL→∞,可以证明,这种情况下的反射系数 Γ=1\Gamma=1Γ=1,驻波比也是无穷大的。由式(2.36)得出线上的电压和电流为
V(z)=Vo+(e−jβz+ejβz)=2Vo+cosβz(2.46a) V(z)=V_{o}^{+}\left(e^{-j\beta z}+e^{j\beta z}\right)=2 V_{o}^{+}\cos\beta z \quad(2.46a) V(z)=Vo+(e−jβz+ejβz)=2Vo+cosβz(2.46a)
图2.7 终端开路的传输线
I(z)=Vo+Z0(e−jβz−ejβz)=−2jVo+Z0sinβz(2.46b) I(z)=\frac{V_{o}^{+}}{Z_{0}}\left(e^{-j\beta z}-e^{j\beta z}\right)=\frac{-2 j V_{o}^{+}}{Z_{0}}\sin\beta z \quad(2.46b) I(z)=Z0Vo+(e−jβz−ejβz)=Z0−2jVo+sinβz(2.46b)
它表明在负载处 I=0I=0I=0,而正如对开路所预料的那样,电压取极大值。利用(2.44)求输入阻抗为
Zin=−jZ0cotβℓ(2.46c) Z_{\text{in}}=-j Z_{0} \cot \beta \ell \quad(2.46c) Zin=−jZ0cotβℓ(2.46c)
对任意长度 ℓ\ellℓ,它也是纯虚数。开路线的电压、电流和输入阻抗已绘于图2.8中。
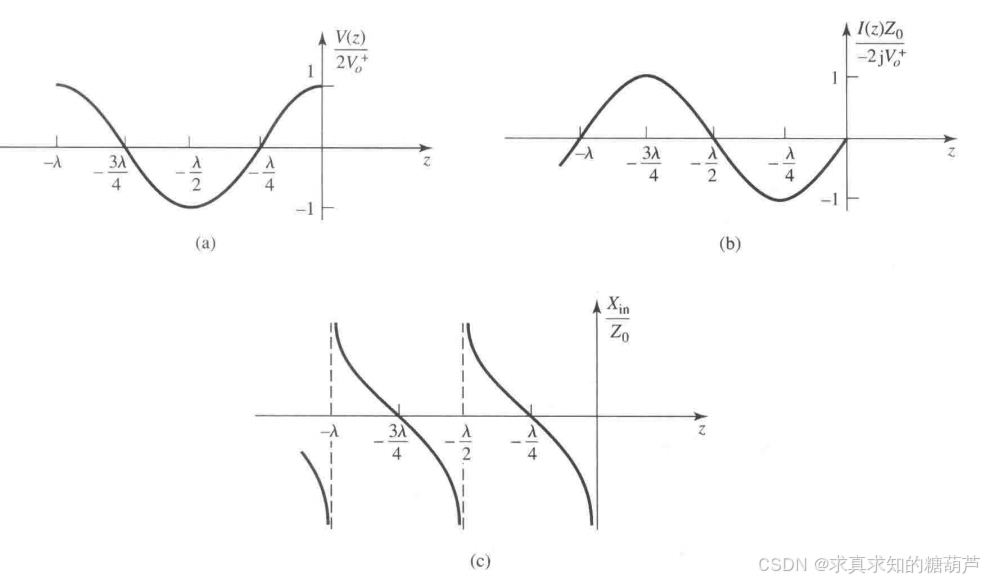
图2.8 (a)电压、(b)电流和(c)阻抗(Rin=0或∞)沿开路传输线的变化
现在考虑一些特定长度的端接传输线。若 ℓ=λ/2\ell=\lambda/2ℓ=λ/2,则式(2.44)表明
Zin=ZL(2.47) Z_{\text{in}}=Z_{L} \quad(2.47) Zin=ZL(2.47)
这意味着半波长(或 λ/2\lambda/2λ/2 的任意整数倍)线不改变或不变换负载阻抗,无论该传输线的特征阻抗是多少。
若线的长度是 1/41/41/4 波长,或更一般地有 ℓ=λ/4+nλ/2\ell=\lambda/4+n\lambda/2ℓ=λ/4+nλ/2,n=1,2,3,...n=1, 2, 3, \ldotsn=1,2,3,...,则式(2.44)表明,输入阻抗由下式给出:
Zin =Z02ZL(2.48) Z_{\text {in }}=\frac{Z_{0}^{2}}{Z_{L}} \qquad (2.48) Zin =ZLZ02(2.48)
这样的传输线称为1/41/41/4 波长变换器,它具有以倒数方式变换负载阻抗的作用,当然也依赖于传输线的特征阻抗。2.5节将更深入地研究这种情况。
现在考虑特征阻抗为 Z0Z_{0}Z0 的传输线馈接到具有不同特征阻抗 Z1Z_{1}Z1 的传输线上的情形,如图2.9所示。若负载线无穷长,或者说它端接到自身的特征阻抗的线上,则没有反射来自其终端,于是由馈线看到的输入阻抗是 Z1Z_{1}Z1,因而反射系数 Γ\GammaΓ 是
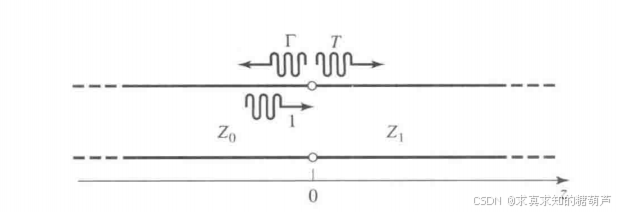
图2.9 具有不同特征阻抗的两段传输线的交接处的反射和传输
Γ=Z1−Z0Z1+Z0(2.49) \Gamma=\frac{Z_{1}-Z_{0}}{Z_{1}+Z_{0}} \qquad (2.49) Γ=Z1+Z0Z1−Z0(2.49)
当一段特性阻抗为 (Z0Z_0Z0) 的无耗传输线连接到另一段特性阻抗为 Z1Z_1Z1 的无耗传输线时,在交接处(z=0z=0z=0)会发生波的反射和传输。设从左侧(z<0z<0z<0)入射的电压波为Vi(z)=Vo+e−jβzV_i(z)=V_o^+ e^{-j\beta z}Vi(z)=Vo+e−jβz,其中Vo+V_o^+Vo+是入射波振幅,β\betaβ 为相位常数(假设两段线具有相同的β\betaβ)。在交接处,部分波被反射,部分波传入第二段线。
在z<0z<0z<0 区域(第一段线),总电压为入射波与反射波之和:
V1(z)=Vo+e−jβz+ΓVo+ejβz=Vo+(e−jβz+Γejβz)(2.50a) V_1(z) = V_o^+ e^{-j\beta z} + \Gamma V_o^+ e^{j\beta z} = V_o^+ \left(e^{-j\beta z} + \Gamma e^{j\beta z}\right) \tag{2.50a} V1(z)=Vo+e−jβz+ΓVo+ejβz=Vo+(e−jβz+Γejβz)(2.50a)
总电流为:
I1(z)=Vo+Z0e−jβz−ΓVo+Z0ejβz=Vo+Z0(e−jβz−Γejβz) I_1(z) = \frac{V_o^+}{Z_0} e^{-j\beta z} - \frac{\Gamma V_o^+}{Z_0} e^{j\beta z} = \frac{V_o^+}{Z_0} \left(e^{-j\beta z} - \Gamma e^{j\beta z}\right) I1(z)=Z0Vo+e−jβz−Z0ΓVo+ejβz=Z0Vo+(e−jβz−Γejβz)
其中 Γ\GammaΓ 是电压反射系数。
在 z>0z>0z>0区域(第二段线),假设只有向右传输的波,无反射(即第二段线无限长或匹配),电压和电流为:
V2(z)=TVo+e−jβz(2.50b) V_2(z) = T V_o^+ e^{-j\beta z} \tag{2.50b} V2(z)=TVo+e−jβz(2.50b)
I2(z)=TVo+Z1e−jβz I_2(z) = \frac{T V_o^+}{Z_1} e^{-j\beta z} I2(z)=Z1TVo+e−jβz
其中T是电压传输系数,表示入射波传到Z1Z_1Z1的幅度与原入射波之比(待求)。
我们有如下边界条件电压电流两个连续性条件
在交接处z=0z=0z=0,电压和电流必须连续:
V1(0)=V2(0),I1(0)=I2(0) V_1(0) = V_2(0), \quad I_1(0) = I_2(0) V1(0)=V2(0),I1(0)=I2(0)
代入表达式得:
Vo+(1+Γ)=TVo+⇒1+Γ=T(A) V_o^+ (1 + \Gamma) = T V_o^+ \quad \Rightarrow \quad 1 + \Gamma = T \tag{A} Vo+(1+Γ)=TVo+⇒1+Γ=T(A)
Vo+Z0(1−Γ)=TVo+Z1⇒1−ΓZ0=TZ1(B) \frac{V_o^+}{Z_0} (1 - \Gamma) = \frac{T V_o^+}{Z_1} \quad \Rightarrow \quad \frac{1 - \Gamma}{Z_0} = \frac{T}{Z_1} \tag{B} Z0Vo+(1−Γ)=Z1TVo+⇒Z01−Γ=Z1T(B)
将式 (A) 代入式 (B):
1−ΓZ0=1+ΓZ1 \frac{1 - \Gamma}{Z_0} = \frac{1 + \Gamma}{Z_1} Z01−Γ=Z11+Γ
这里同样解得反射系数,验证了我们刚刚的分析:
Γ=Z1−Z0Z1+Z0(2.49) \Gamma = \frac{Z_1 - Z_0}{Z_1 + Z_0} \tag{2.49} Γ=Z1+Z0Z1−Z0(2.49)
将 Γ\GammaΓ 代入式 (A) 得传输系数:
T=1+Γ=1+Z1−Z0Z1+Z0=Z1+Z0+Z1−Z0Z1+Z0=2Z1Z1+Z0(2.51) T = 1 + \Gamma = 1 + \frac{Z_1 - Z_0}{Z_1 + Z_0} = \frac{Z_1 + Z_0 + Z_1 - Z_0}{Z_1 + Z_0} = \frac{2Z_1}{Z_1 + Z_0} \tag{2.51} T=1+Γ=1+Z1+Z0Z1−Z0=Z1+Z0Z1+Z0+Z1−Z0=Z1+Z02Z1(2.51)
电路中两点间的传输系数常常用单位 dB 表示成插入损耗(Insertion Loss, IL):
IL=−20lg∣T∣ dB(2.52) IL=-20\lg\left|T\right| \text{ dB} \qquad (2.52) IL=−20lg∣T∣ dB(2.52)
小结一下:**反射系数 Γ\GammaΓ衡量入射波在交接处被反射的比例** 。当Z1=Z0Z_1 = Z_0Z1=Z0时,Γ=0\Gamma=0Γ=0,无反射,全匹配。传输系数TTT 衡量入射波电压传入第二段线的比例 。注意电压传输系数可大于1(当Z1>Z0Z_1 > Z_0Z1>Z0时),但功率传输系数不会大于1 。入射功率 Pinc=∣Vo+∣2/(2Z0)P_{\text{inc}} = |V_o^+|^2/(2Z_0)Pinc=∣Vo+∣2/(2Z0),反射功率 Prefl=∣Γ∣2PincP_{\text{refl}} = |\Gamma|^2 P_{\text{inc}}Prefl=∣Γ∣2Pinc,传输功率 Ptrans=∣T∣2∣Vo+∣2/(2Z1)P_{\text{trans}} = |T|^2 |V_o^+|^2/(2Z_1)Ptrans=∣T∣2∣Vo+∣2/(2Z1)。可验证Pinc=Prefl+PtransP_{\text{inc}} = P_{\text{refl}} + P_{\text{trans}}Pinc=Prefl+Ptrans。
兴趣点:分贝和奈培
在微波系统中两功率电平 P1P_{1}P1 和 P2P_{2}P2 之比经常用分贝(dB)表示为
10lgP1P2 dB 10\lg\frac{P_{1}}{P_{2}}\mathrm{~dB} 10lgP2P1 dB
因此功率比为 2 等效于 3 dB,功率比为 0.1 等效于 -10 dB。用 dB 表示的功率比使得计算通过一系列元件后的功率损耗或增益比较容易,因为对数运算相乘的损耗或增益因子可以通过对每一级用分贝表示的损耗或增益的相加来计算。例如,一个信号经过一个 6 dB 的衰减器和一个 23 dB 的放大器后将具有 23-6=17 dB 的总增益。
分贝仅用来表示功率比,但是若 P1=V12/R1P_{1}=V_{1}^{2}/R_{1}P1=V12/R1,P2=V22/R2P_{2}=V_{2}^{2}/R_{2}P2=V22/R2,则用电压比来表示的功率比是
10lgV12R2V22R1=20lgV1V2R2R1 dB 10\lg\frac{V_{1}^{2}R_{2}}{V_{2}^{2}R_{1}}=20\lg\frac{V_{1}}{V_{2}}\sqrt{\frac{R_{2}}{R_{1}}} \mathrm{~dB} 10lgV22R1V12R2=20lgV2V1R1R2 dB
式中 R1R_{1}R1 和 R2R_{2}R2 为负载电阻,V1V_{1}V1 和 V2V_{2}V2 为这些负载上的电压。若负载电阻相等,则该公式简化为
20lgV1V2 dB 20\lg\frac{V_{1}}{V_{2}}\mathrm{~dB} 20lgV2V1 dB
相等电阻两端的电压之比也可用奈培(Np)表示为
lnV1V2Np \ln\frac{V_{1}}{V_{2}}\mathrm{Np} lnV2V1Np
用功率表示的对应表达式是
12lnP1P2Np \frac{1}{2}\ln\frac{P_{1}}{P_{2}}\mathrm{Np} 21lnP2P1Np
因为电压正比于功率的平方根。传输线的衰减有时用奈培表示。因为 1 Np 对应于功率比 e2\mathrm{e}^{2}e2,所以奈培和分贝之间的转换关系是
分贝(dB)和奈培(Np)都是用于表示比值的对数单位,常用于描述信号幅度、功率等的相对变化。它们之间的换算关系可以通过电压比或功率比的定义推导得到。
分贝定义:
LdB=10lg(P1P2) dB L_{\text{dB}} = 10 \lg\left(\frac{P_1}{P_2}\right) \ \text{dB} LdB=10lg(P2P1) dB
其中lg\lglg表示以 10 为底的对数。对于电压比(或电流比),在相同负载电阻条件下根据P∝V2P \propto V^2P∝V2有
LdB=20lg(V1V2) dB L_{\text{dB}} = 20 \lg\left(\frac{V_1}{V_2}\right) \ \text{dB} LdB=20lg(V2V1) dB
奈培定义式为:
LNp=ln(V1V2) Np L_{\text{Np}} = \ln\left(\frac{V_1}{V_2}\right) \ \text{Np} LNp=ln(V2V1) Np
其中ln\lnln表示自然对数。对于功率比,则有
LNp=12ln(P1P2) Np L_{\text{Np}} = \frac{1}{2} \ln\left(\frac{P_1}{P_2}\right) \ \text{Np} LNp=21ln(P2P1) Np
设电压比 A=V1/V2A = V_1 / V_2A=V1/V2,则根据定义:
- 奈培数:N=lnAN = \ln AN=lnA(单位:Np)
- 分贝数:D=20lgAD = 20 \lg AD=20lgA(单位:dB)
将分贝表达式中的转化为自然对数:
D=20lgA=20⋅lnAln10=20ln10⋅lnA=20ln10⋅N D = 20 \lg A = 20 \cdot \frac{\ln A}{\ln 10} = \frac{20}{\ln 10} \cdot \ln A = \frac{20}{\ln 10} \cdot N D=20lgA=20⋅ln10lnA=ln1020⋅lnA=ln1020⋅N
因此,
D=20ln10⋅N≈8.685889638⋅N D = \frac{20}{\ln 10} \cdot N \approx 8.685889638 \cdot N D=ln1020⋅N≈8.685889638⋅N
即:
1 Np=20ln10 dB≈8.686 dB 1 \ \text{Np} = \frac{20}{\ln 10} \ \text{dB} \approx 8.686 \ \text{dB} 1 Np=ln1020 dB≈8.686 dB
所以
1 奈培 (Np) ≈ 8.686 分贝 (dB)
1 分贝 (dB) ≈ 0.1151 奈培 (Np)
若一个参考功率电平是已知的,则绝对功率也可以用分贝符号来表示。若令 P2=1mWP_{2}=1\mathrm{mW}P2=1mW,则功率 P1P_{1}P1 可以用 dBm 表示为
10lgP11 mWdBm 10\lg\frac{P_{1}}{1\mathrm{~mW}}\mathrm{dBm} 10lg1 mWP1dBm
因此,1 mW 的功率是 0 dBm,而 1 W 的功率是 30 dBm,等等。