SRGAN 源代码:https://github.com/leftthomas/SRGAN.git
SRGAN 论文:https://arxiv.org/abs/1609.04802
GAN 提供了一个强大的框架,能够生成具有高感知质量、外观逼真的自然图像。其训练机制促使重建结果向搜索空间中更可能包含照片级真实图像的区域移动,从而更接近自然图像流形(如图 3 所示)。
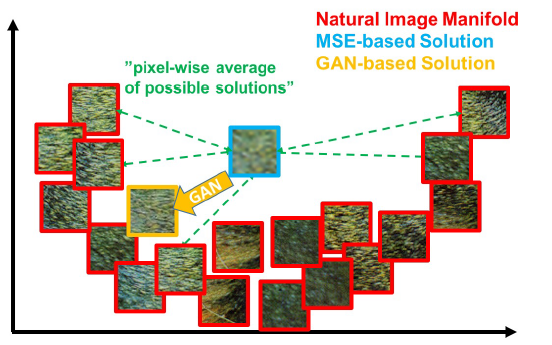
图 3:基于 MSE 超分辨率重建的图像块(蓝色)以及基于 GAN 超分辨率重建的图像块(橙色)示意图。基于 MSE 的解由于在像素空间中对所有可能解进行了像素级平均,导致结果过度平滑;而 GAN 则将重建结果推向自然图像流形,从而生成在感知上更具真实感的解。
本文首次提出一种基于 GAN 概念的极深 ResNet 架构 [29, 30],通过构建一种感知损失函数来实现照片级真实的单图像超分辨率(SISR)。我们的主要贡献如下:
我们提出了一种包含 16 个残差块的深度 ResNet(称为 SRResNet),该网络针对均方误差(MSE)进行优化,在高倍放大因子(4×)下,以 PSNR 和结构相似性(SSIM)为指标,为图像超分辨率任务设立了新的性能标杆。
我们提出了 SRGAN------一种基于 GAN 的网络,其优化目标是一种新型的感知损失。在此方法中,我们摒弃了传统的 MSE 内容损失,转而采用在 VGG 网络 [49] 特征图上计算的损失,该损失对像素空间的变化更具不变性 [38]。
我们在三个公开基准数据集的图像上进行了大规模平均主观意见分(MOS)测试,结果表明:在高倍放大因子(4×)下生成照片级真实超分辨率图像的任务中,SRGAN 以显著优势成为当前最先进的方法。
Method
在单图像超分辨率(SISR)任务中,目标是从低分辨率输入图像 I L R I^{LR} ILR 估计出对应的高分辨率超分辨率图像 I S R I^{SR} ISR。其中, I L R I^{LR} ILR 是其高分辨率对应图像 I H R I^{HR} IHR 的低分辨率版本。高分辨率图像 I H R I^{HR} IHR 仅在训练阶段可用。在训练过程中, I L R I^{LR} ILR 通过对 I H R I^{HR} IHR 应用高斯滤波器,再进行下采样(下采样因子为 r r r)而获得。对于具有 C C C 个颜色通道的图像,我们用一个大小为 W × H × C W \times H \times C W×H×C 的实值张量表示 I L R I^{LR} ILR,而 I H R I^{HR} IHR 和 I S R I^{SR} ISR 则分别由大小为 r W × r H × C rW \times rH \times C rW×rH×C 的张量表示。
我们的最终目标是训练一个生成函数 G G G,使其能够为给定的低分辨率输入图像估计出对应的高分辨率图像。为此,我们将生成器网络建模为一个前馈卷积神经网络 G θ G G_{\theta_G} GθG,其参数为 θ G \theta_G θG。这里, θ G = { W 1 : L , b 1 : L } \theta_G = \{W_{1:L}, b_{1:L}\} θG={W1:L,b1:L} 表示一个 L L L 层深度网络的权重和偏置,通过优化一个面向超分辨率的特定损失函数 ℓ S R \ell^{SR} ℓSR 获得。对于训练图像对 { I n H R , I n L R } \{I^{HR}_n, I^{LR}_n\} {InHR,InLR}(其中 n = 1 , ... , N n = 1, \dots, N n=1,...,N),我们求解如下优化问题:
θ ^ G = arg min θ G 1 N ∑ n = 1 N ℓ S R ( G θ G ( I n L R ) , I n H R ) ( 1 ) \hat{\theta}G = \arg\min{\theta_G} \frac{1}{N} \sum_{n=1}^{N} \ell^{SR}\big(G_{\theta_G}(I^{LR}_n), I^{HR}_n\big) \quad (1) θ^G=argθGminN1n=1∑NℓSR(GθG(InLR),InHR)(1)
在本文中,我们将特别设计一种感知损失 ℓ S R \ell^{SR} ℓSR,将其表示为多个损失分量的加权组合,每个分量分别建模超分辨率重建图像所应具备的不同理想特性。
Adversarial network architecture
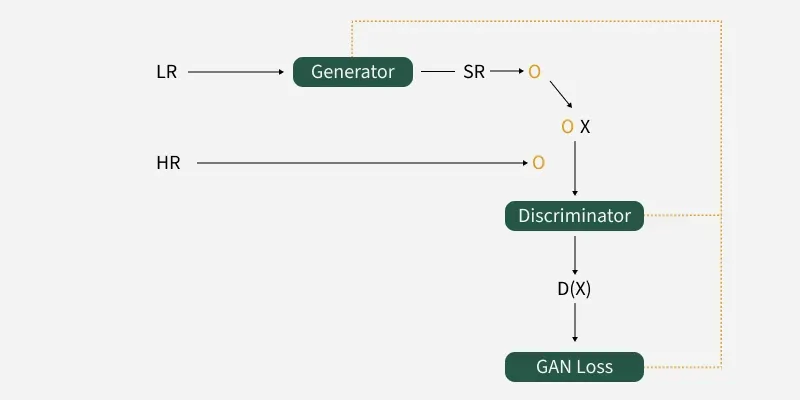
遵循 Goodfellow 等人[22]的方法,我们进一步定义了一个判别器网络 D θ D D_{\theta_D} DθD,并将其与生成器 G θ G G_{\theta_G} GθG以交替优化的方式联合训练,以求解如下对抗性的极小-极大问题:
min θ G max θ D E I H R ∼ p train ( I H R ) [ log D θ D ( I H R ) ] + E I L R ∼ p G ( I L R ) [ log ( 1 − D θ D ( G θ G ( I L R ) ) ) ] ( 2 ) \min_{\theta_G}\max_{\theta_D}\ \mathbb{E}{I^{HR}\sim p{\text{train}}(I^{HR})}[\log D_{\theta_D}(I^{HR})]+\mathbb{E}{I^{LR}\sim p_G(I{LR})}[\log(1-D_{\theta_D}(G_{\theta_G}(I^{LR})))]\quad(2) θGminθDmax EIHR∼ptrain(IHR)[logDθD(IHR)]+EILR∼pG(ILR)[log(1−DθD(GθG(ILR)))](2)
该公式的根本思想在于:通过训练一个可微的判别器 D D D(其目标是区分超分辨率重建图像与真实高分辨率图像),来引导生成模型 G G G学会"欺骗"判别器。借助这一机制,生成器能够学习生成与真实图像高度相似的样本,使得判别器难以将其正确分类。这促使生成结果落入自然图像流形(manifold)所张成的子空间中,从而获得感知质量更优的超分辨率图像。这与通过最小化像素级误差(如均方误差MSE)所得到的超分辨率结果形成鲜明对比------后者往往过度平滑,缺乏真实感。
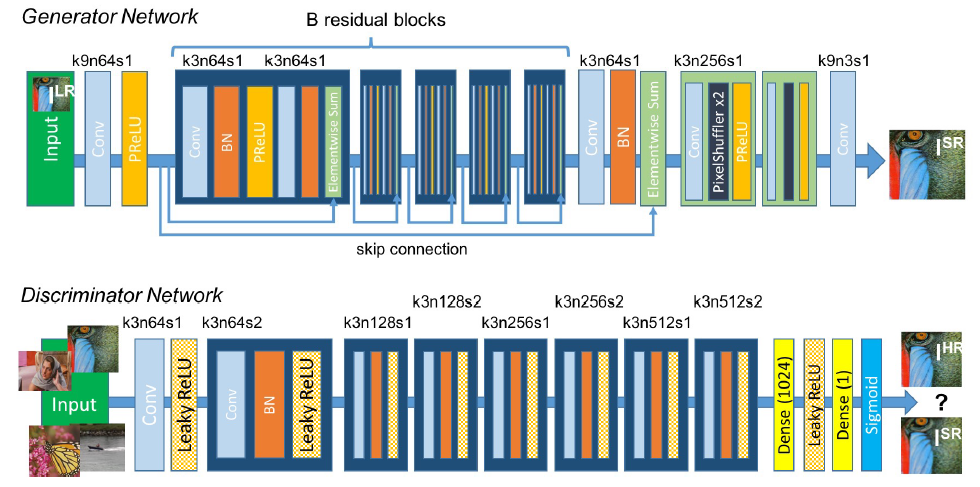
图4:生成器与判别器网络架构,其中每个卷积层均标注了对应的卷积核大小(k)、特征图数量(n)和步长(s)。
如图4所示,我们所采用的极深生成器网络 G G G的核心由 B B B个结构相同的残差块(residual blocks)堆叠而成。受Johnson等人[33]的启发,我们采用了Gross和Wilber[24]提出的残差块设计:每个块包含两个卷积层,使用较小的 3 × 3 3\times3 3×3卷积核和64个特征图,后接批归一化层(Batch Normalization)[32]和ParametricReLU(PReLU)[28]激活函数。为了提升图像分辨率,我们采用Shi等人[48]提出的子像素卷积层(sub-pixel convolution layers),通过两个可训练的上采样层实现分辨率放大。
为区分真实高分辨率图像与生成的超分辨率样本,我们同时训练一个判别器网络,其架构如图4所示。我们遵循Radford等人[44]总结的架构准则:全网络使用LeakyReLU激活函数(斜率 α = 0.2 \alpha=0.2 α=0.2),并避免使用最大池化(max-pooling)。该判别器用于求解公式(2)中的最大化问题,共包含8个卷积层,每层的 3 × 3 3\times3 3×3卷积核数量逐层翻倍(从64增至512,与VGG网络[49]类似)。每当特征图数量翻倍时,便使用带步长的卷积(strided convolution)对图像分辨率进行下采样。最后,512个特征图经过两个全连接层,并通过一个Sigmoid激活函数输出样本属于"真实图像"的概率。
Perceptual loss function
我们感知损失函数 l S R l_{SR} lSR的定义对生成器网络的性能至关重要。虽然 l S R l_{SR} lSR通常基于均方误差(MSE)[10,48]进行建模,但我们改进了Johnson等人[33]和Bruna等人[5]的工作,设计了一种能够从感知相关特性 角度评估重建结果的损失函数。我们将感知损失表示为内容损失( l X S R l_{X}^{SR} lXSR)与对抗损失分量的加权和,形式如下:
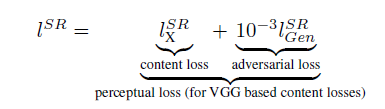
接下来,我们将分别介绍内容损失 l X S R l_{X}^{SR} lXSR和对抗损失 l G e n S R l_{Gen}^{SR} lGenSR的可能设计选择。
内容损失
像素级均方误差(MSE)损失定义如下:
l M S E S R = 1 r 2 W H ∑ x = 1 r W ∑ y = 1 r H ( I H R x , y − G θ G ( I L R ) x , y ) 2 ( 4 ) l_{MSE}^{SR}=\frac{1}{r^2WH}\sum_{x=1}^{rW}\sum_{y=1}^{rH}(I_{HR}^{x,y}-G_{\theta_G}(I_{LR})^{x,y})^2\quad(4) lMSESR=r2WH1x=1∑rWy=1∑rH(IHRx,y−GθG(ILR)x,y)2(4)
这是图像超分辨率任务中最广泛使用的优化目标,许多当前最先进的方法均依赖于此[10,48]。然而,尽管MSE优化方案通常能获得较高的PSNR值,其结果往往缺乏高频细节 ,导致感知质量不佳,纹理过度平滑(参见图2)。

图2:从左至右依次为:双三次插值、针对MSE优化的深度残差网络、针对更符合人类感知的损失函数优化的深度残差生成对抗网络、原始高分辨率(HR)图像。括号中给出了对应的PSNR和SSIM值。[4×放大]
为克服这一问题,我们不再依赖像素级损失,而是借鉴Gatys等人[19]、Bruna等人[5]以及Johnson等人[33]的思想,采用一种更贴近人类感知相似性 的损失函数。我们基于Simonyan和Zisserman[49]提出的预训练19层VGG网络中的ReLU激活层来定义VGG损失。记 ϕ i , j \phi_{i,j} ϕi,j为VGG19网络中第 i i i个最大池化层之前的第 j j j个卷积层(激活后)所得到的特征图(视为已知)。于是,我们将VGG损失定义为重建图像 G θ G ( I L R ) G_{\theta_G}(I_{LR}) GθG(ILR)与参考图像 I H R I_{HR} IHR在特征表示上的欧氏距离:
l V G G : i , j S R = 1 W i , j H i , j ∑ x = 1 W i , j ∑ y = 1 H i , j ( ϕ i , j ( I H R ) x , y − ϕ i , j ( G θ G ( I L R ) ) x , y ) 2 ( 5 ) l_{VGG:i,j}^{SR}=\frac{1}{W_{i,j}H_{i,j}}\sum_{x=1}^{W_{i,j}}\sum_{y=1}^{H_{i,j}}(\phi_{i,j}(I^{HR})^{x,y}-\phi_{i,j}(G_{\theta_G}(I^{LR}))^{x,y})^2\quad(5) lVGG:i,jSR=Wi,jHi,j1x=1∑Wi,jy=1∑Hi,j(ϕi,j(IHR)x,y−ϕi,j(GθG(ILR))x,y)2(5)
其中, W i , j W_{i,j} Wi,j和 H i , j H_{i,j} Hi,j分别表示VGG网络中对应特征图的空间维度。
对抗损失
除了上述内容损失外,我们还将GAN的生成部分引入感知损失中。这促使网络倾向于生成位于自然图像流形上的解,即通过"欺骗"判别器网络来优化生成结果。生成损失 l G e n S R l_{Gen}^{SR} lGenSR基于判别器对所有训练样本的输出概率定义如下:
l G e n S R = ∑ n = 1 N − log D θ D ( G θ G ( I L R ) ) ( 6 ) l_{Gen}^{SR}=\sum_{n=1}^{N}-\log D_{\theta_D}(G_{\theta_G}(I^{LR}))\quad(6) lGenSR=n=1∑N−logDθD(GθG(ILR))(6)
其中, D θ D ( G θ G ( I L R ) ) D_{\theta_D}(G_{\theta_G}(I_{LR})) DθD(GθG(ILR))表示重建图像 G θ G ( I L R ) G_{\theta_G}(I_{LR}) GθG(ILR)被判定为自然高分辨率图像的概率。为获得更稳定的梯度,我们最小化 − log D θ D ( G θ G ( I L R ) ) -\log D_{\theta_D}(G_{\theta_G}(I^{LR})) −logDθD(GθG(ILR)),而非 log [ 1 − D θ D ( G θ G ( I L R ) ) ] \log[1-D_{\theta_D}(G_{\theta_G}(I^{LR}))] log[1−DθD(GθG(ILR))][22]。
实验
数据集与相似性度量
我们在三个广泛使用的基准数据集上进行实验:Set5 [3]、Set14 [69] 和 BSD100(即 BSD300 的测试集)[41]。所有实验均采用 4× 的超分辨率尺度因子,对应图像像素数量减少 16 倍。
为确保公平比较,所有报告的 PSNR [dB] 和 SSIM [58] 指标均基于 中心裁剪后的图像 y 通道 计算,并移除每条边 4 像素宽的边界,使用 daala 工具包¹ 实现。
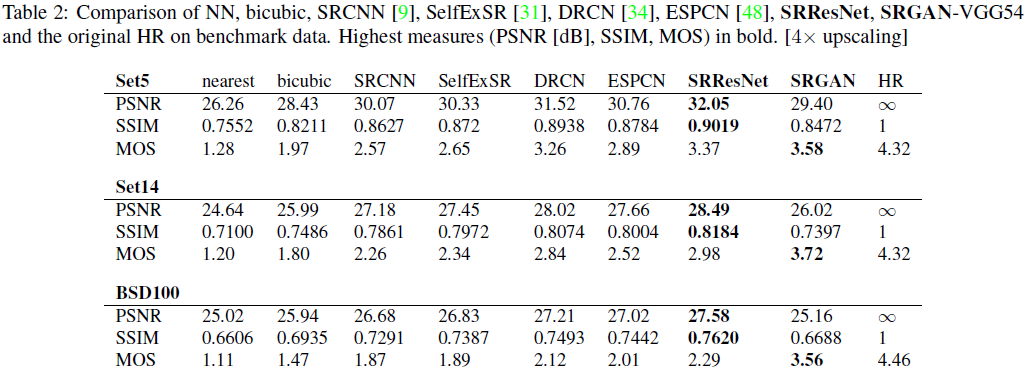
参考方法(包括最近邻、双三次插值、SRCNN [9] 和 SelfExSR [31])的超分辨率结果来自 Huang 等人² [31] 提供的在线补充材料;DRCN 的结果来自 Kim 等人³ [34]。本文提出的 SRResNet(分别使用 l M S E S R l_{MSE}^{SR} lMSESR 和 l V G G : 2 , 2 S R l_{VGG:2,2}^{SR} lVGG:2,2SR 损失)以及 SRGAN 各变体的结果已公开⁴。
统计显著性检验采用配对双侧 Wilcoxon 符号秩检验 ,显著性水平设为 p < 0.05 p < 0.05 p<0.05。
读者可能也会对 GitHub 上一个独立开发的基于 GAN 的方案⁵ 感兴趣。但该方案仅在有限的人脸数据集上提供了实验结果,而人脸超分是一个约束更强、难度更低的任务。
¹ https://github.com/xiph/daala (commit: 8d03668)
² https://github.com/jbhuang0604/SelfExSR
³ http://cv.snu.ac.kr/research/DRCN/
⁴ https://twitter.box.com/s/lcue6vlrd01ljkdtdkhmfvk7vtjhetog
⁵ https://github.com/david-gpu/srez
训练细节与参数
所有网络均在 NVIDIA Tesla M40 GPU 上训练,训练数据来自 ImageNet 数据库 [45] 中随机采样的 35 万张图像 ,且与测试图像无重叠。低分辨率(LR)图像通过对高分辨率(HR)图像(BGR 格式, C = 3 C=3 C=3)使用双三次核下采样(下采样因子 r = 4 r=4 r=4)获得。
每个 mini-batch 随机裁剪 16 张 96×96 的 HR 子图像 ,每张来自不同的训练图像。由于生成器是全卷积网络,可处理任意尺寸的输入图像。
- LR 输入图像的像素值被缩放到 [0, 1];
- HR 图像的像素值被缩放到 [-1, 1];
- 因此,MSE 损失在 [-1, 1] 范围内计算。
为使 VGG 损失与 MSE 损失量级相当,VGG 特征图被额外缩放 1 / 12.75 1/12.75 1/12.75 倍(等价于将公式 (5) 乘以约 0.006 的缩放因子)。
优化器采用 Adam [36]( β 1 = 0.9 \beta_1 = 0.9 β1=0.9):
- SRResNet 使用学习率 10 − 4 10^{-4} 10−4,训练 10 6 10^6 106 次迭代;
- 训练 SRGAN 时,先用 MSE 优化的 SRResNet 初始化生成器,以避免陷入不良局部最优;
- 所有 SRGAN 变体先以 10 − 4 10^{-4} 10−4 学习率训练 10 5 1 0^5 105 次迭代,再以更低的学习率 10 − 5 10^{-5} 10−5 继续训练 10 5 10^5 105 次迭代。
生成器与判别器交替更新 (即 Goodfellow 等人 [22] 中的 k = 1 k=1 k=1 策略)。生成器网络包含 16 个相同的残差块 ( B = 16 B=16 B=16)。
测试阶段关闭批归一化(Batch Normalization)的更新,以确保输出仅由输入决定,具有确定性 [32]。
本实现基于 Theano [53] 和 Lasagne [8]。
MOS测试
我们进行了平均主观意见分(MOS)测试,以量化不同方法在重建感知上逼真图像 方面的能力。具体而言,我们邀请了 26 名评分者 ,对超分辨率重建图像按 1(质量差)到 5(质量优秀) 的整数等级进行打分。
每位评分者需对 Set5、Set14 和 BSD100 数据集中的每张图像的 12 种版本 进行评分,包括:
- 最近邻插值(NN)
- 双三次插值(Bicubic)
- SRCNN [9]
- SelfExSR [31]
- DRCN [34]
- ESPCN [48]
- SRResNet-MSE
- SRResNet-VGG22*(*在 BSD100 上未评分)
- SRGAN-MSE*
- SRGAN-VGG22*
- SRGAN-VGG54
- 原始高分辨率(HR)图像
因此,每位评分者共需评估 1128 个样本 (19 张图像 × 12 种版本 + 100 张图像 × 9 种版本),所有图像以随机顺序呈现。
在正式测试前,评分者使用 BSD300 训练集中的 20 张图像 进行校准:其中 NN 版本固定评为 1 分,HR 版本固定评为 5 分。
在一项预实验中,我们通过在更大测试集中重复加入同一方法的图像两次 ,对 26 名评分者在 BSD100 的 10 张图像子集上的校准流程和重测信度(test-retest reliability)进行了评估。结果表明评分具有良好的一致性,且对相同图像的两次评分无显著差异。
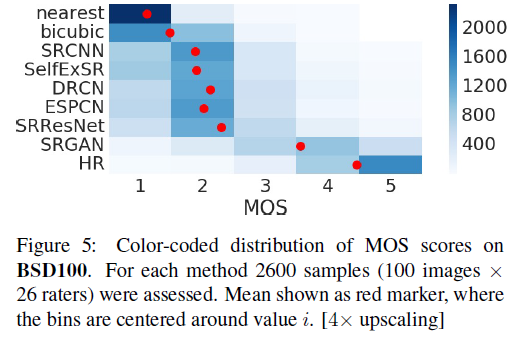
评分者对 NN 插值图像高度一致地评为 1 分 ,对原始 HR 图像高度一致地评为 5 分(参见图 5)。
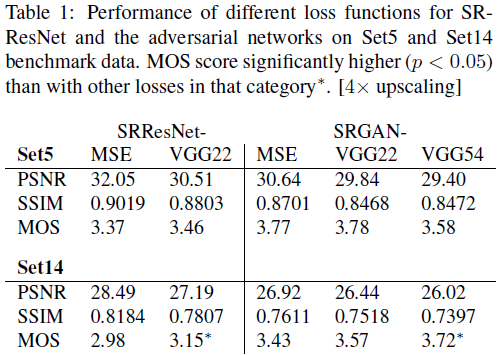
本次 MOS 测试的实验结果汇总于 表 1、表 2 和图 5。
内容损失的消融研究
我们研究了在基于 GAN 的网络中,不同内容损失选择 对感知损失的影响。
具体而言,我们考察以下形式的感知损失:
l S R = l X S R + 10 − 3 l G e n S R l_{SR} = l_X^{SR} + 10^{-3} l_{Gen}^{SR} lSR=lXSR+10−3lGenSR
其中内容损失 l X S R l_X^{SR} lXSR 分别采用以下三种形式:
- SRGAN-MSE :使用 l M S E S R l_{MSE}^{SR} lMSESR 作为内容损失,以验证在标准 MSE 损失下引入对抗训练的效果;
- SRGAN-VGG22 :使用 l V G G : 2 , 2 S R l_{VGG:2,2}^{SR} lVGG:2,2SR,即基于 VGG 网络中较浅层特征图 ϕ 2 , 2 \phi_{2,2} ϕ2,2 的损失,该特征主要反映低层视觉特征 [68];
- SRGAN-VGG54 :使用 l V G G : 5 , 4 S R l_{VGG:5,4}^{SR} lVGG:5,4SR,即基于 VGG 网络深层特征图 ϕ 5 , 4 \phi_{5,4} ϕ5,4 的损失,该特征更能捕捉图像的高层语义内容 [68, 65, 40]。
在下文中,我们将此模型简称为 SRGAN。
此外,我们还评估了无对抗组件的生成器网络性能,分别使用:
- l M S E S R l_{MSE}^{SR} lMSESR(记为 SRResNet-MSE ,后文简称为 SRResNet);
- l V G G : 2 , 2 S R l_{VGG:2,2}^{SR} lVGG:2,2SR(记为 SRResNet-VGG22)。
值得注意的是,在训练 SRResNet-VGG22 时,我们在 l V G G : 2 , 2 S R l_{VGG:2,2}^{SR} lVGG:2,2SR 基础上额外加入了权重为 2 × 10 − 8 2 \times 10^{-8} 2×10−8 的全变分损失(Total Variation Loss)[2, 33]。
定量结果汇总于表 1 ,可视化示例见图 6 。

实验表明:即使结合对抗损失,MSE 仍能获得最高的 PSNR 值 ,但其重建结果在感知上过于平滑、缺乏真实感 ,不如那些采用对视觉感知更敏感的损失所得到的结果。
这一现象源于 MSE 内容损失与对抗损失之间的目标冲突。我们还在少数 SRGAN-MSE 的重建结果中观察到轻微的伪影,也归因于这种目标竞争。
在 Set5 数据集上,我们未能发现某种损失函数在 MOS 评分上显著优于其他方法。
然而,在 Set14 上,SRGAN-VGG54 显著优于其他所有 SRGAN 和 SRResNet 变体 (MOS 评分最高)。
我们观察到一个明显趋势:使用高层 VGG 特征图 ϕ 5 , 4 \phi_{5,4} ϕ5,4 比 ϕ 2 , 2 \phi_{2,2} ϕ2,2 能生成更丰富的纹理细节(参见图 6)。