(leetcode) 力扣100 52腐烂的橘子（BFS）

题目

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；

值 1 代表新鲜橘子；

值 2 代表腐烂的橘子。

每分钟，腐烂的橘子周围 4 个方向上相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

数据范围

m == grid.length

n == grid[i].length

1 <= m, n <= 10

grid[i][j] 仅为 0、1或 2

测试用例

示例1

java 复制代码

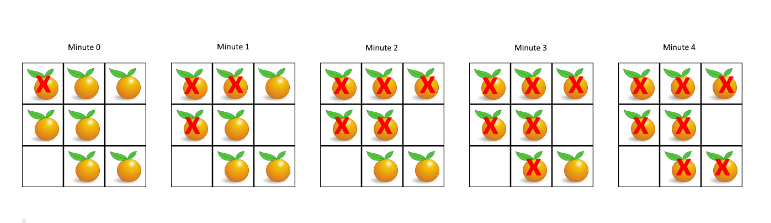
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例2

java 复制代码

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例3

java 复制代码

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

题解（BFS 时空Omn）

java 复制代码

class Solution {
    // 定义位移数组，方便处理上下左右四个方向
    int move[][] = {{0, 1, 0, -1}, {1, 0, -1, 0}};
    int oneNum = 0; // 用于统计新鲜橘子的总数

    public int orangesRotting(int[][] grid) {
        // 边界处理：如果网格为空，直接返回 0
        if (grid == null || grid.length == 0) {
            return 0;
        }

        int c = grid.length;    // 行数
        int l = grid[0].length; // 列数
        Queue<Integer> queue = new LinkedList<>();

        // 1. 初始化扫描：将所有初始腐烂橘子放入队列，统计新鲜橘子数量
        for (int i = 0; i < c; i++) {
            for (int j = 0; j < l; j++) {
                if (grid[i][j] == 2) {
                    // 使用一维索引 (i * l + j) 压缩二维坐标节省空间
                    queue.add(i * l + j);
                }
                if (grid[i][j] == 1) {
                    oneNum++;
                }
            }
        }

        // 特殊情况处理
        if (queue.size() == 0 && oneNum != 0) {
            return -1; // 有新鲜橘子但没有腐烂源，永远无法腐烂
        } else if (oneNum == 0) {
            return 0;  // 没有新鲜橘子，不需要等待时间
        }

        int res = 0; // 记录时间（分钟/层数）
        // 2. 开启 BFS 逐层扩散
        while (!queue.isEmpty()) {
            int num = queue.size(); // 当前层的腐烂橘子数量
            res++; 
            while (num-- != 0) {
                int pos = queue.poll();
                int x = pos / l; // 解码回行坐标
                int y = pos % l; // 解码回列坐标
                
                // 检查四个方向
                for (int k = 0; k < 4; k++) {
                    int tx = x + move[0][k];
                    int ty = y + move[1][k];
                    
                    // 如果邻居在边界内且是新鲜橘子
                    if (tx >= 0 && tx < c && ty >= 0 && ty < l && grid[tx][ty] == 1) {
                        grid[tx][ty] = 2; // 标记为腐烂，防止重复访问
                        queue.add(tx * l + ty); // 加入下一层扩散队列
                        oneNum--; // 新鲜橘子减少
                    }
                }
            }
        }
        
        // 3. 结果判断
        // res-1 是因为最后一层橘子扩散完后，queue 虽然为空，但 res 还是多加了一次
        return oneNum != 0 ? -1 : res - 1;
    }
}

思路

这道题虽然是普通题，但实际上思路很简单，可能是因为橘子这道题太经典了吧，反正用个BFS遍历就行，需要注意的就是无法扩散情况，这种情况下创建一个变量记录新鲜橘子数量即可。