重走力扣hot的矩阵

矩阵置零

螺旋矩阵

矩阵置零

73. 矩阵置零 - 力扣（LeetCode）

法一：

引入两个HashSet容器，分别记录元素为0的横坐标与纵坐标

空：O（M+N）

代码

复制代码

   class Solution_2026_1_26_1 {
        int m;
        int n;
        public void setZeroes(int[][] matrix) {
            Set<Integer> row_zero=new HashSet();
            Set<Integer> col_zero=new HashSet();
            m=matrix.length;
            n=matrix[0].length;
            for(int i=0;i<m;i++){
                for(int j=0;j<n;j++){
                    if(matrix[i][j]==0){
                        row_zero.add(i);
                        col_zero.add(j);
                    }
                }
            }
            for(int i=0;i<m;i++){
                for(int j=0;j<n;j++){
                    //Set无get方法
                    if(row_zero.contains(i)||col_zero.contains(j)){
                        matrix[i][j]=0;
                    }

                }
            }


        }
    }

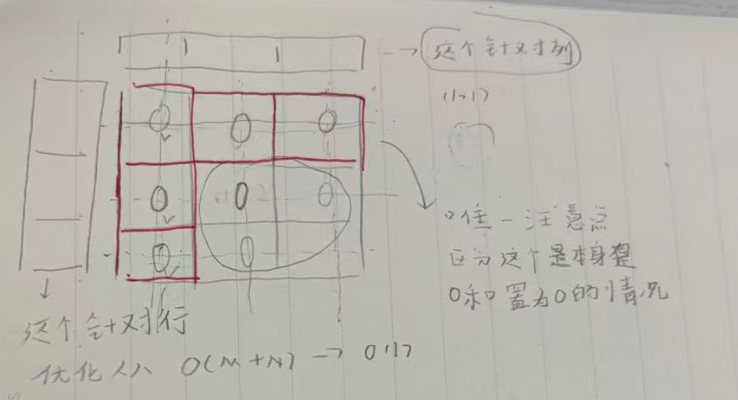
优化：空间复杂度优化为O(1)

重点：区分第一行和第一列的0是本身就是0还是被修改为0的

java 复制代码

class Solution {
    public void setZeroes(int[][] matrix) {
        //进行优化 空间复杂度降低为O(1)
        boolean hasRowZero=false;
        boolean hasColZero=false;
        int m=matrix.length;
        int n=matrix[0].length;
         //检查第一行是否有为0的
         for(int i=0;i<n;i++){
            //检查第一行是否为空 
            //但本质上第一行处理的是列
            if(matrix[0][i]==0){
                hasRowZero=true;
                break;
            }
         }

            for(int i=0;i<m;i++){
            //检查第一列是否为空 
            //但本质上第一列处理的是行
            if(matrix[i][0]==0){
                hasColZero=true;
                break;
            }
         }
         //遍历二维数组 进行标记
         for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(matrix[i][j]==0){
                    matrix[0][j]=0;
                    matrix[i][0]=0;
                }
            }
         }

         for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(matrix[0][j]==0||matrix[i][0]==0){
                    matrix[i][j]=0;
                }
            }
         }
         //单独处理第一行为0的情况
         if(hasRowZero){
            for(int i=0;i<n;i++){
                matrix[0][i]=0;
            }
         }

         if(hasColZero){
            for(int i=0;i<m;i++){
                matrix[i][0]=0;
            }
         }
        
    }
}

螺旋矩阵

54. 螺旋矩阵 - 力扣（LeetCode）

个人认为关键点就是理清除过程，先从左往右处理上边界，然后从上往下处理右边界，然后从右往左处理下边界，最后在从下往上处理左边界即可，理清楚过程即可

java 复制代码

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m=matrix.length;
        int n=matrix[0].length;
        List<Integer> ret=new ArrayList<>();
        int left=0;
        int right=n-1;
        int top=0;
        int bottom=m-1;
        while(left<=right&&top<=bottom){
            for(int i=left;i<=right;i++){
                ret.add(matrix[top][i]); //从左往右处理
            }
            top++; //从上往下
            for(int i=top;i<=bottom;i++){
                ret.add(matrix[i][right]); //从下往上处理
            }
            right--; //从后往前
            if(top<=bottom){
                for(int i=right;i>=left;i--){
                    //从后往前
                    ret.add(matrix[bottom][i]);
                }
                //从下往上
                bottom--;
            }
            if(left<=right){
                for(int i=bottom;i>=top;i--){
                    ret.add(matrix[i][left]);
                }
                //从前往后
                left++;
            }
        }
        return ret;
    
    }
}