设 ADADAD, BFBFBF, CECECE 为 △ABC\triangle ABC△ABC 的边长. QQQ 是 EFEFEF 上的一点, 且满足 QF=DEQF=DEQF=DE, 且 FFF 位于 EEE, QQQ 之间. PPP 是 EFEFEF 上的一点, 且满足 EP=DFEP=DFEP=DF, 且 EEE 位于 PPP, FFF 之间. DQDQDQ 的垂直平分线与 ABABAB 在 XXX 点相交, DPDPDP 的垂直平分线与 ACACAC 在 YYY 点相交. 证明 BCBCBC 的中点位于 XYXYXY 上. (2016, 伊朗数学奥林匹克国家队选拔赛)
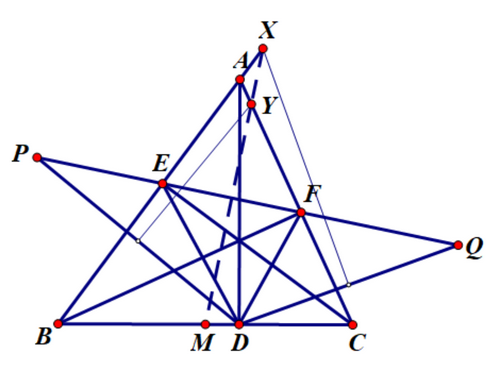
证明:
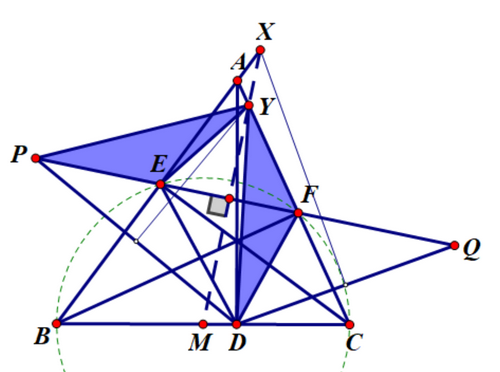
设 BCBCBC 的中点为 MMM, MMM 在 EFEFEF 的中垂线上, 设 EFEFEF 的中垂线交 ABABAB 于 X′X'X′, 交 ACACAC 于 Y′Y'Y′.
EY′=FY′EY'=FY'EY′=FY′, ∠Y′EP=∠Y′FE=π−B=∠Y′FD\angle Y'EP=\angle Y'FE=\pi-B=\angle Y'FD∠Y′EP=∠Y′FE=π−B=∠Y′FD, PE=DFPE=DFPE=DF, 所以 △PEY′≃△DFY′\triangle PEY' \simeq \triangle DFY'△PEY′≃△DFY′.
YYY 在 PDPDPD 的中垂线上, 所以 Y′Y'Y′ 即为 YYY.
同理, X′X'X′ 即为 XXX.
证毕.