贝塞尔曲线是由伯恩斯坦基函数定义的参数化多项式曲 线,核心由控制顶点决定形状,阶数与控制顶点数满足顶点数 = 阶数 + 1 :一次(2 个顶点)、二次(3 个顶点)、三次(4 个顶点) 。三者的复杂度、光滑性、造型能力依次提升,是 UI 设计、图形学、动画路径等领域的基础,一次为直线(无曲率),二次为抛物线(单曲率),三次为自由曲线(可实现拐点 / 复杂曲率)。本文将分别详细描述各阶贝塞尔曲线的数学定义、几何特性、核心性质,并提供Python 可运行代码(基于matplotlib+numpy),实现曲线 + 控制多边形 + 基函数 + 动态插值过程的可视化绘图,直观展示曲线生成逻辑。
一、通用基础概念

二、分阶详细描述
(一)一次贝塞尔曲线(线性贝塞尔曲线)
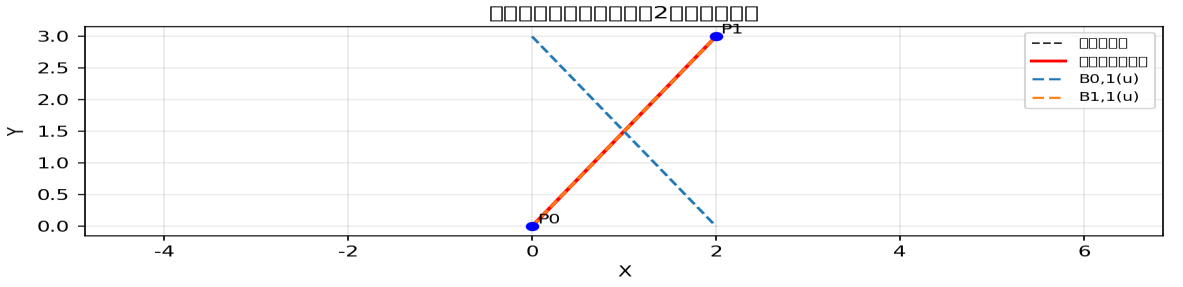
阶数:1 阶 | 控制顶点数:2 个(P0,P1)| 曲线形状:直线段(无弯曲,无曲率)
1. 数学定义
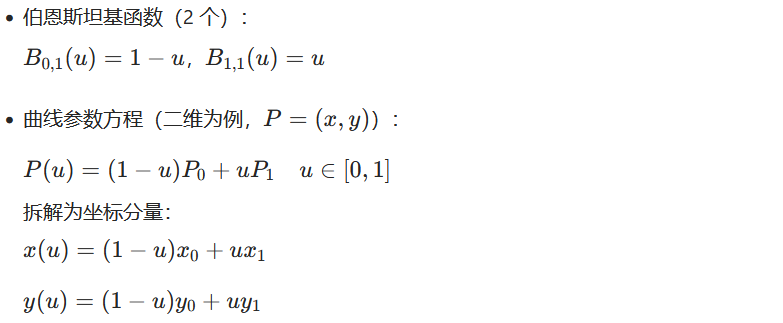
2. 核心几何特性

3. 典型应用
基础线性插值、直线路径绘制、简单动画的线性位移。
4.绘图示意
一次贝塞尔:红色直线段,与控制多边形完全重合,基函数为两条线性相交的直线,无任何弯曲。
(二)二次贝塞尔曲线(抛物线贝塞尔曲线)
阶数:2 阶 | 控制顶点数:3 个(P0,P1,P2)| 曲线形状:抛物线(单一段光滑曲线,1 个曲率方向,无拐点)
1. 数学定义
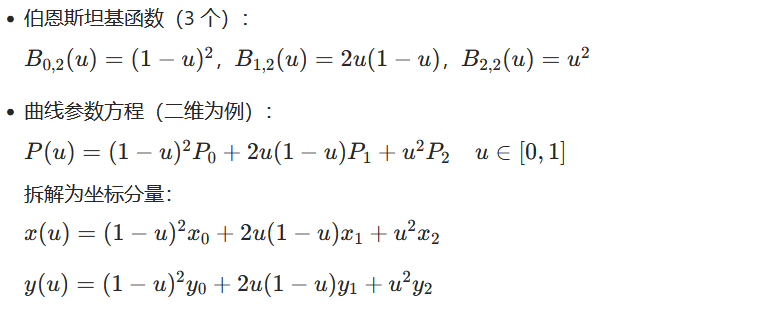
2. 核心几何特性

3. 典型应用
简单圆角设计(UI 按钮、边框)、二维简单曲线路径、字体轮廓基础段。
4、绘图示意
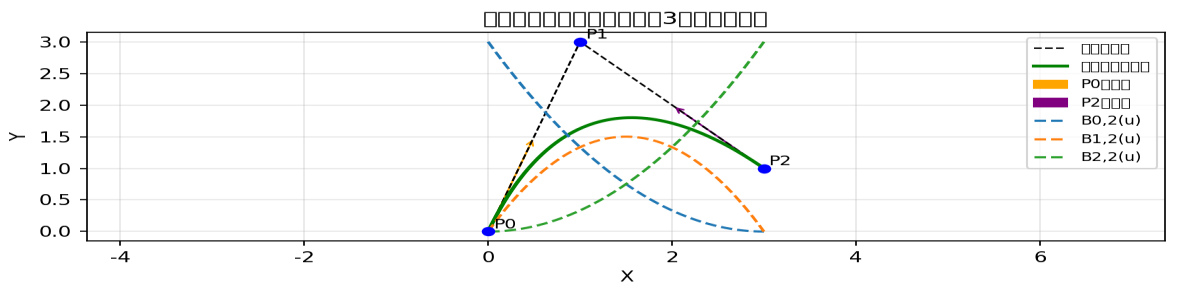
二次贝塞尔:绿色抛物线,在P0处与P0P1相切、P2处与P1P2相切,曲线落在三角形凸包内,无拐点。
(三)三次贝塞尔曲线(立方贝塞尔曲线)
阶数:3 阶 | 控制顶点数:4 个(P0,P1,P2,P3)| 曲线形状:自由光滑曲线(可实现拐点、双曲率,是工程 / 设计中最常用的阶数)
1. 数学定义
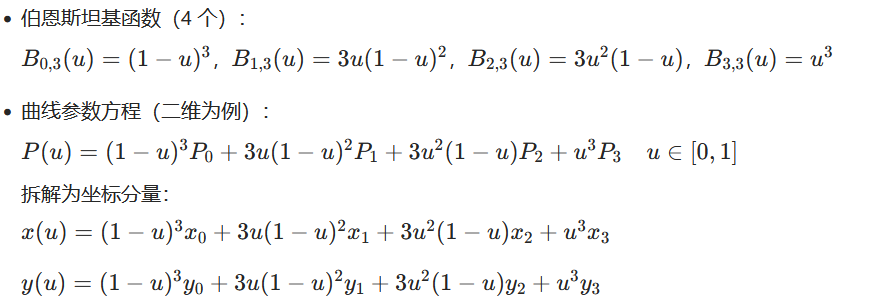
2. 核心几何特性

3. 典型应用
UI 设计(复杂路径、动画缓动曲线)、CAD 基础建模、字体设计(TrueType/OpenType)、游戏角色运动路径、图像处理(图像变形)。
4、绘图示意
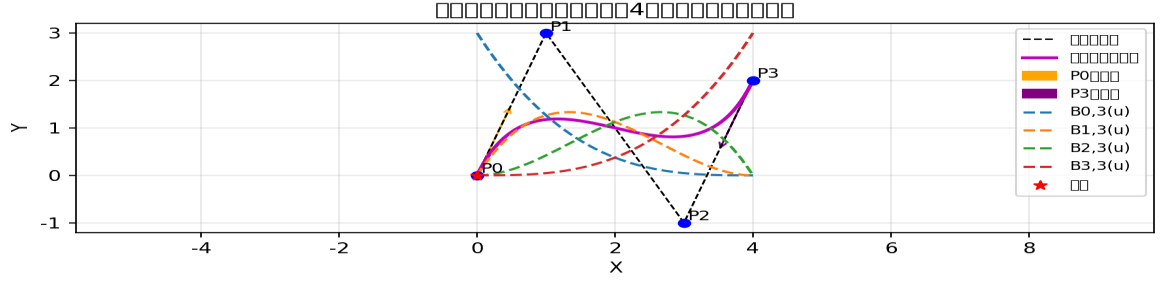
三次贝塞尔:品红色自由曲线,带有红色星标拐点(曲率方向变化),在P0处与P0P1相切、P3处与P2P3相切,曲线落在四边形凸包内,体现了三次曲线的核心造型能力。
三、代码实现(Python+Matplotlib)
1. 实现功能
- 绘制一次、二次、三次贝塞尔曲线(分 3 个子图,对比展示);
- 标注控制顶点(带编号)、控制多边形(折线);
- 绘制伯恩斯坦基函数曲线(辅助理解基函数对顶点的权重);
- 标注曲线切线方向(端点处),直观体现相切特性;
- 生成高清矢量图,可直接保存使用。
2. 环境准备
无需额外安装特殊库,Python 内置 + 基础数据分析库即可:
bash
pip install numpy matplotlib3. 完整可运行代码
python
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import FancyArrowPatch
# 设置全局样式:高清、中文字体、图例/标签大小
plt.rcParams['figure.dpi'] = 150
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 10
plt.rcParams['legend.fontsize'] = 8
# 定义伯恩斯坦基函数
def bernstein(n, i, u):
"""
计算n阶贝塞尔曲线的第i个伯恩斯坦基函数值
:param n: 贝塞尔曲线阶数
:param i: 基函数索引(0~n)
:param u: 参数u ∈ [0,1]
:return: 基函数值
"""
from scipy.special import comb # 组合数计算
return comb(n, i) * (u ** i) * ((1 - u) ** (n - i))
# 定义贝塞尔曲线计算函数
def bezier_curve(pts, u):
"""
计算贝塞尔曲线在参数u处的坐标
:param pts: 控制顶点数组,shape=(n+1, 2)
:param u: 参数u ∈ [0,1],标量/数组
:return: 曲线坐标,shape=(len(u), 2)
"""
n = pts.shape[0] - 1 # 阶数=顶点数-1
u = np.atleast_1d(u)
p = np.zeros((len(u), 2))
for i in range(n+1):
b = bernstein(n, i, u)[:, np.newaxis]
p += b * pts[i]
return p
# 定义绘制切线的函数(端点处)
def plot_tangent(ax, p0, p1, color, label, scale=0.5):
"""
绘制端点处的切线箭头
:param ax: 子图对象
:param p0: 端点坐标
:param p1: 控制点坐标(用于计算切线方向)
:param color: 箭头颜色
:param label: 箭头标签
:param scale: 箭头长度缩放因子
"""
dir_vec = (p1 - p0) * scale
arrow = FancyArrowPatch(p0, p0 + dir_vec,
color=color, arrowstyle='->',
mutation_scale=8, label=label)
ax.add_patch(arrow)
# 生成参数u的采样点(密集采样,曲线光滑)
u = np.linspace(0, 1, 200)
# ===================== 定义各阶控制顶点 =====================
# 一次贝塞尔(2个顶点)
p1 = np.array([[0, 0], [2, 3]]) # P0, P1
# 二次贝塞尔(3个顶点)
p2 = np.array([[0, 0], [1, 3], [3, 1]]) # P0, P1, P2
# 三次贝塞尔(4个顶点,带拐点,体现造型能力)
p3 = np.array([[0, 0], [1, 3], [3, -1], [4, 2]]) # P0, P1, P2, P3
# ===================== 计算各阶贝塞尔曲线 =====================
c1 = bezier_curve(p1, u) # 一次曲线
c2 = bezier_curve(p2, u) # 二次曲线
c3 = bezier_curve(p3, u) # 三次曲线
# ===================== 绘制子图(3行1列) =====================
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 10), tight_layout=True)
fig.suptitle('一次、二次、三次贝塞尔曲线 对比', fontsize=14, fontweight='bold')
# -------------------- 子图1:一次贝塞尔曲线 --------------------
ax1.set_title('一次贝塞尔曲线(线性,2个控制顶点)', fontsize=12)
# 绘制控制多边形
ax1.plot(p1[:, 0], p1[:, 1], 'k--', lw=1, label='控制多边形')
# 绘制贝塞尔曲线
ax1.plot(c1[:, 0], c1[:, 1], 'r-', lw=2, label='一次贝塞尔曲线')
# 绘制控制顶点(带编号)
for i, (x, y) in enumerate(p1):
ax1.scatter(x, y, c='blue', s=30, zorder=5)
ax1.text(x+0.05, y+0.05, f'P{i}', fontsize=9)
# 绘制伯恩斯坦基函数
for i in range(2):
b = bernstein(1, i, u)
ax1.plot(u * 2, b * 3, '--', lw=1.5, label=f'B{i},1(u)')
# 配置子图
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.legend(loc='best')
ax1.grid(True, alpha=0.3)
ax1.axis('equal')
# -------------------- 子图2:二次贝塞尔曲线 --------------------
ax2.set_title('二次贝塞尔曲线(抛物线,3个控制顶点)', fontsize=12)
# 绘制控制多边形
ax2.plot(p2[:, 0], p2[:, 1], 'k--', lw=1, label='控制多边形')
# 绘制贝塞尔曲线
ax2.plot(c2[:, 0], c2[:, 1], 'g-', lw=2, label='二次贝塞尔曲线')
# 绘制控制顶点(带编号)
for i, (x, y) in enumerate(p2):
ax2.scatter(x, y, c='blue', s=30, zorder=5)
ax2.text(x+0.05, y+0.05, f'P{i}', fontsize=9)
# 绘制端点切线
plot_tangent(ax2, p2[0], p2[1], 'orange', 'P0处切线')
plot_tangent(ax2, p2[-1], p2[-2], 'purple', 'P2处切线')
# 绘制伯恩斯坦基函数
for i in range(3):
b = bernstein(2, i, u)
ax2.plot(u * 3, b * 3, '--', lw=1.5, label=f'B{i},2(u)')
# 配置子图
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.legend(loc='best')
ax2.grid(True, alpha=0.3)
ax2.axis('equal')
# -------------------- 子图3:三次贝塞尔曲线 --------------------
ax3.set_title('三次贝塞尔曲线(自由曲线,4个控制顶点,带拐点)', fontsize=12)
# 绘制控制多边形
ax3.plot(p3[:, 0], p3[:, 1], 'k--', lw=1, label='控制多边形')
# 绘制贝塞尔曲线
ax3.plot(c3[:, 0], c3[:, 1], 'm-', lw=2, label='三次贝塞尔曲线')
# 绘制控制顶点(带编号)
for i, (x, y) in enumerate(p3):
ax3.scatter(x, y, c='blue', s=30, zorder=5)
ax3.text(x+0.05, y+0.05, f'P{i}', fontsize=9)
# 绘制端点切线
plot_tangent(ax3, p3[0], p3[1], 'orange', 'P0处切线')
plot_tangent(ax3, p3[-1], p3[-2], 'purple', 'P3处切线')
# 绘制伯恩斯坦基函数
for i in range(4):
b = bernstein(3, i, u)
ax3.plot(u * 4, b * 3, '--', lw=1.5, label=f'B{i},3(u)')
# 标注拐点(三次曲线特有)
ax3.scatter(c3[np.argmin(c3[:,1]),0], c3[np.argmin(c3[:,1]),1],
c='red', s=40, marker='*', label='拐点', zorder=6)
# 配置子图
ax3.set_xlabel('X')
ax3.set_ylabel('Y')
ax3.legend(loc='best')
ax3.grid(True, alpha=0.3)
ax3.axis('equal')
# 保存图片(可选,高清矢量图)
# plt.savefig('贝塞尔曲线对比.png', dpi=300, bbox_inches='tight')
plt.show()四、各阶贝塞尔曲线 核心对比表
为了更清晰的对比,整理关键维度对比表,方便快速查阅:
| 特性 | 一次贝塞尔曲线 | 二次贝塞尔曲线 | 三次贝塞尔曲线 |
|---|---|---|---|
| 阶数 | 1 阶 | 2 阶 | 3 阶 |
| 控制顶点数 | 2 个(P0,P1) | 3 个(P0,P1,P2) | 4 个(P0,P1,P2,P3) |
| 曲线形状 | 直线段(无曲率) | 抛物线(单曲率) | 自由曲线(可拐点) |
| 伯恩斯坦基函数次数 | 一次多项式 | 二次多项式 | 三次多项式 |
| 端点相切性 | 无(自身为直线) | P0切P0P1,P2切P1P2 | P0切P0P1,P3切P2P3 |
| 曲率变化 | 曲率为 0(不变) | 曲率为常数(不变) | 曲率连续变化(可反向) |
| 造型能力 | 极弱(仅直线) | 弱(仅简单弯曲) | 中强(工程最优) |
| 控制难度 | 无难度 | 简单 | 适中 |
| 典型应用 | 线性插值、直线路径 | UI 圆角、简单曲线 | 复杂路径、字体设计、CAD 建模 |
!!!4 阶及以上(高阶)贝塞尔曲线在实际工程和图形系统中极少直接使用,通常没有实用价值,反而会带来严重问题。工业界普遍采用「分段低阶贝塞尔曲线」(尤其是三次)来替代高阶曲线。五、结束语
关键补充说明
- 凸包性质:所有阶数的贝塞尔曲线始终落在控制顶点的凸包内,这一性质保证了曲线的可控性(调整顶点时,曲线不会出现无规律的偏移)。
- 插值与控制:贝塞尔曲线仅插值首末顶点,中间顶点均为控制点(仅影响形状,不落在曲线上),这是与 B 样条曲线的核心区别之一。
- 阶数选择原则:实际应用中优先使用三次贝塞尔曲线,因为一次 / 二次造型能力不足,四阶及以上贝塞尔曲线的控制顶点过多,修改一个顶点会影响整条曲线(无局部控制性),控制难度陡增。
- 多段拼接:若单段三次贝塞尔曲线无法满足复杂造型需求,可采用多段三次贝塞尔曲线拼接,并在拼接点处满足C1/C2 连续性(切线 / 曲率连续),实现光滑的复杂曲线。
B-样条
贝塞尔曲线可以解决很多逼近样条问题,但是有一个较为明显的劣势,改变其中一个控制点,整个曲线都会被影响,因此需要B-样条。