FA_拟合和插值(FI,fitting_and_interpolation)-逼近样条01(贝塞尔、B样条和NURBS曲线)

首先：贝塞尔曲线 ⊂ B - 样条曲线 ⊂ NURBS 曲线，三者是层层包含、逐步泛化的关系，NURBS 曲线是前两者的通用形式，能够兼容表示贝塞尔曲线和 B - 样条曲线。

一、先明确核心定义

逼近样条曲线（Spline）是一组分段光滑、在连接点处满足一定连续性条件（通常是 C¹、C² 连续）的曲线段的集合，最初源于工程绘图中用「样条尺」绘制的光滑曲线，后来被数学建模为参数化曲线，核心目的是用简单的数学表达式拟合复杂的光滑轮廓。

参数化样条曲线的通用形式：

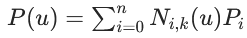
其中：

• u为参数；
• Pi为控制顶点；
• Ni,k(u)为基函数；

三种曲线的核心区别就是基函数的类型和约束条件不同。

1. 贝塞尔曲线（Bezier Curve）

• 核心定义 ：一种无节点（或说节点固定）的参数化多项式曲线，由一组控制顶点P0​,P1​,...,Pn​（n为阶数，通常说的 n 次贝塞尔曲线）定义，基函数为伯恩斯坦多项式（Bernstein Polynomial）。

• 数学表达式 （n 次贝塞尔曲线）：
  

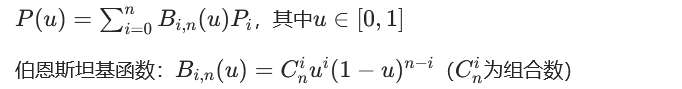
• 关键约束（局限性）：

  • 控制顶点数 = 阶数 + 1，n 次曲线对应 n+1 个控制顶点，阶数过高时曲线难以控制。
  • 无局部控制性：修改任意一个控制顶点，都会影响整条曲线的形状。
  • 参数区间固定为[0,1]，仅能表示单段光滑曲线。
  • 曲线必然经过首末两个控制顶点（P(0)=P0，P(1)=Pn），且与首末控制边相切。

2. B - 样条曲线（B-Spline Curve）

• 核心定义 ：对贝塞尔曲线的泛化，引入节点向量（Knot Vector） ，基函数为B 样条基函数（由德布尔 - 考克斯递推公式定义），支持分段定义曲线，解决了贝塞尔曲线无局部控制性的问题。

• 数学表达式 ：
  

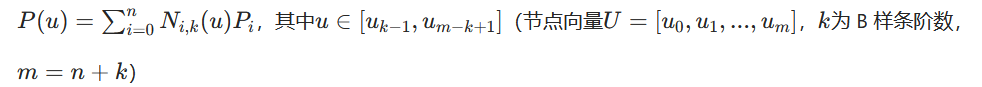
• 关键约束（相对于贝塞尔曲线的改进）：

  • 引入节点向量，节点将参数区间划分为多个子区间，每个子区间对应一段曲线，仅由相邻的k个控制顶点决定。
  • 局部控制性：修改某个控制顶点，仅影响曲线的局部一段（相邻k个节点区间对应的曲线段）。
  • 支持多段光滑拼接，连续性由阶数k和节点重复度决定（节点重复度≤k时，可保证Ck−r−1连续，r为节点重复度）。
  • 可以兼容表示贝塞尔曲线（满足特定节点向量约束即可）。

3. NURBS 曲线（Non-Uniform Rational B-Spline Curve）

• 核心定义 ：对 B - 样条曲线的进一步泛化，引入权因子（Weight），基函数为有理 B 样条基函数，解决了 B 样条曲线无法精确表示圆锥曲线（圆、椭圆、抛物线、双曲线）的问题。
• 数学表达式 ：
• 关键约束 （相对于 B - 样条曲线的改进）：
  • 引入权因子，当所有权因子wi=1时，退化为普通 B - 样条曲线。
  • 可精确表示圆锥曲线和初等曲面（贝塞尔、B - 样条仅能近似表示）。
  • 保持 B - 样条曲线的局部控制性、分段光滑性等所有优点。
  • 是计算机辅助设计（CAD）、图形学中的标准曲线表示方法（如 AutoCAD、UG 等软件均采用）。

二、三者的包含关系与转换（条目化，核心重点）

1. 包含关系（层层泛化，从特殊到一般）

贝塞尔曲线 ⊂ B-样条曲线 ⊂ NURBS曲线

具体对应关系：

曲线类型	能否被后续曲线兼容表示	兼容条件（核心）
贝塞尔曲线	能被 B - 样条曲线表示	1. 节点向量采用「夹紧节点」（首末节点重复k次）；2. 节点数m=n+k（n为贝塞尔控制顶点数 - 1，k为 B 样条阶数 = 贝塞尔阶数）
贝塞尔曲线	能被 NURBS 曲线表示	满足 B - 样条兼容条件 + 所有权因子wi​=1
B - 样条曲线	能被 NURBS 曲线表示	所有权因子wi​=1（有理部分退化为 1，即为普通 B - 样条）

2. 具体转换方法（条目化，可落地）

（1）贝塞尔曲线 → B - 样条曲线

（2）B - 样条曲线 → NURBS 曲线

（3）贝塞尔曲线 → NURBS 曲线

（4）特殊说明：反向转换（NURBS→B - 样条→贝塞尔）

三、代码示例（使用 Python 的geomdl库，专业几何建模库）

1. 环境准备

geomdl是专门用于几何建模（曲线、曲面）的 Python 库，完美支持贝塞尔、B - 样条、NURBS 曲线的定义和转换，先安装：

pip install geomdl

2. 代码示例：三者的定义、转换与可视化

from geomdl import BSpline, NURBS, Bezier
from geomdl import utilities
from geomdl.visualization import VisMPL

# =============================================
# 示例1：定义贝塞尔曲线（3次，4个控制顶点）
# =============================================
print("=== 步骤1：定义3次贝塞尔曲线 ===")
bezier_curve = Bezier.Curve()
# 设置阶数（3次，对应4个控制顶点）
bezier_curve.degree = 3
# 设置控制顶点（二维平面点，可改为三维）
control_points_bezier = [
    (0.0, 0.0),   # P0
    (1.0, 3.0),   # P1
    (3.0, 4.0),   # P2
    (5.0, 2.0)    # P3
]
bezier_curve.ctrlpts = control_points_bezier
# 自动生成参数区间（贝塞尔默认[0,1]）
bezier_curve.knotvector = utilities.generate_knot_vector(bezier_curve.degree, len(bezier_curve.ctrlpts))
# 采样曲线点（用于可视化，增加采样数使曲线更光滑）
bezier_curve.sample_size = 100

# =============================================
# 示例2：贝塞尔曲线 → B-样条曲线（按转换规则）
# =============================================
print("\n=== 步骤2：贝塞尔曲线转换为B-样条曲线 ===")
bspline_curve = BSpline.Curve()
# 1. 复用贝塞尔的阶数
bspline_curve.degree = bezier_curve.degree
# 2. 复用贝塞尔的控制顶点
bspline_curve.ctrlpts = bezier_curve.ctrlpts
# 3. 构造夹紧节点向量（与贝塞尔的knotvector一致，geomdl已自动支持）
bspline_curve.knotvector = bezier_curve.knotvector
# 采样曲线点
bspline_curve.sample_size = 100

# =============================================
# 示例3：B-样条曲线 → NURBS曲线（按转换规则）
# =============================================
print("\n=== 步骤3：B-样条曲线转换为NURBS曲线 ===")
nurbs_curve = NURBS.Curve()
# 1. 复用B-样条的阶数
nurbs_curve.degree = bspline_curve.degree
# 2. 复用B-样条的控制顶点
nurbs_curve.ctrlpts = bspline_curve.ctrlpts
# 3. 复用B-样条的节点向量
nurbs_curve.knotvector = bspline_curve.knotvector
# 4. 分配权因子w_i=1（所有控制顶点权值为1）
nurbs_curve.weights = [1.0 for _ in range(len(nurbs_curve.ctrlpts))]
# 采样曲线点
nurbs_curve.sample_size = 100

# =============================================
# 示例4：验证三者的一致性（输出关键信息）
# =============================================
print("\n=== 步骤4：验证三者的核心参数一致性 ===")
print(f"贝塞尔曲线阶数：{bezier_curve.degree}")
print(f"B-样条曲线阶数：{bspline_curve.degree}")
print(f"NURBS曲线阶数：{nurbs_curve.degree}")
print(f"贝塞尔控制顶点数：{len(bezier_curve.ctrlpts)}")
print(f"B-样条控制顶点数：{len(bspline_curve.ctrlpts)}")
print(f"NURBS控制顶点数：{len(nurbs_curve.ctrlpts)}")
print(f"贝塞尔节点向量：{bezier_curve.knotvector}")
print(f"B-样条节点向量：{bspline_curve.knotvector}")
print(f"NURBS节点向量：{nurbs_curve.knotvector}")
print(f"NURBS权因子：{nurbs_curve.weights}")

# =============================================
# 示例5：可视化三条曲线（重合，验证转换正确性）
# =============================================
print("\n=== 步骤5：可视化三条曲线（将弹出绘图窗口） ===")
# 合并三条曲线用于批量可视化
from geomdl import MultiCurve
multi_curve = MultiCurve()
multi_curve.add(bezier_curve)
multi_curve.add(bspline_curve)
multi_curve.add(nurbs_curve)
# 设置可视化样式
multi_curve.vis = VisMPL.VisCurve2D()
multi_curve.render()

# =============================================
# 示例6：NURBS曲线的扩展（修改权因子，体现其优势）
# =============================================
print("\n=== 步骤6：修改NURBS权因子，展示其灵活性 ===")
# 复制原NURBS曲线，修改第二个控制顶点的权因子
nurbs_curve_modified = NURBS.Curve()
nurbs_curve_modified.degree = nurbs_curve.degree
nurbs_curve_modified.ctrlpts = nurbs_curve.ctrlpts
nurbs_curve_modified.knotvector = nurbs_curve.knotvector
# 修改第二个控制顶点的权因子为5.0（其余保持1.0）
nurbs_curve_modified.weights = [1.0, 5.0, 1.0, 1.0]
nurbs_curve_modified.sample_size = 100

# 可视化修改后的NURBS曲线（与原曲线对比）
multi_curve_modified = MultiCurve()
multi_curve_modified.add(nurbs_curve)
multi_curve_modified.add(nurbs_curve_modified)
multi_curve_modified.vis = VisMPL.VisCurve2D()
multi_curve_modified.render()

3. 代码运行结果说明

四、补充：关键知识点拓展（条目化）

五、结束语

• 三者是特殊到一般的层层泛化关系：贝塞尔曲线⊂B - 样条曲线⊂NURBS 曲线，核心区别在于基函数和约束条件的不同。
• 转换的核心是复用核心参数（阶数、控制顶点、节点向量）+ 满足兼容条件（夹紧节点、权因子全 1），贝塞尔可直接转为 B - 样条，B - 样条可直接转为 NURBS。
• NURBS 曲线是功能最强大的通用形式，兼具局部控制性和精确表示圆锥曲线的能力，是工程和图形学的主流选择，而geomdl库是实现三者定义、转换和可视化的高效工具。