纽结数据分析（KDA）

纽结数据分析（KDA）

原文：Shen, L., Feng, H., Li, F., Lei, F., Wu, J., and Wei, G.-W., "Knot data analysis using multiscale Gauss link integral", Proceedings of the National Academy of Science, vol. 121, no. 42, Art. no. e2408431121, 2024. doi:10.1073/pnas.2408431121.

这篇发表在PNAS上的文章提出了纽结数据分析 （Knot Data Analysis，KDA）的概念，介绍了对于可以用曲线描述的结构，如何借鉴纽结理论和持续同调的思想，进行拓扑分析（如蛋白质数据）。作者已将文中数据集和代码开源至GitHub，链接：https://github.com/WeilabMSU/mGLI-KDA。同样，我只罗列方法学部分，主要介绍作者到底构造了哪些能表征拓扑结构的量。

文章的逻辑是：先介绍如何刻画两条曲线之间的拓扑特征，然后说明很多实际问题都可以化归到计算两条曲线拓扑特征的问题，从而实现应用。
一、两条曲线的拓扑特征

两条曲线可能以比较复杂的形式"纠缠"在一起，借助作者给的多尺度数据分析手段，可以对曲线之间的相互影响进行描述。总体思路：
高斯链环积分 → 高斯链环积分的分割 → 尺度化高斯链环积分 → 局部化尺度化高斯链环积分 → 特征 高斯链环积分\rightarrow 高斯链环积分的分割\rightarrow 尺度化高斯链环积分\rightarrow 局部化尺度化高斯链环积分\rightarrow 特征 高斯链环积分→高斯链环积分的分割→尺度化高斯链环积分→局部化尺度化高斯链环积分→特征

定义1（高斯链环积分，Gauss linking integral）：对于两条不交曲线 l 1 , l 2 l_1,l_2 l1,l2，参数化为 γ 1 ( s ) , γ 2 ( t ) \gamma_1(s),\gamma_2(t) γ1(s),γ2(t)，则高斯链环积分定义为
L ( l 1 , l 2 ) = 1 4 π ∫ [ 0 , 1 ] ∫ [ 0 , 1 ] d e t ( γ ˙ 1 ( s ) , γ ˙ 2 ( t ) , γ 1 ( s ) − γ 2 ( t ) ) ∣ γ 1 ( s ) − γ 2 ( t ) ∣ 3 d s d t L(l_1,l_2)=\frac{1}{4\pi}\int_{[0,1]}\int_{[0,1]}\frac{det(\dot{\gamma}_1(s),\dot{\gamma}_2(t),\gamma_1(s)-\gamma_2(t))}{|\gamma_1(s)-\gamma_2(t)|^3}dsdt L(l1,l2)=4π1∫[0,1]∫[0,1]∣γ1(s)−γ2(t)∣3det(γ˙1(s),γ˙2(t),γ1(s)−γ2(t))dsdt

它表征了 l 1 l_1 l1 和 l 2 l_2 l2 之间的相互缠绕程度。对于闭合曲线，高斯链环积分是整数且为拓扑不变量；对于开放曲线，高斯链环积分是实数且为曲线坐标的连续函数。

定义2（高斯链环积分的分割，Segmentation of Gauss linking integral）：将 l 1 l_1 l1 和 l 2 l_2 l2 分别用有限段不交曲线 P n = { p 1 , p 2 , ⋯   , p n } P_n=\{p_1,p_2,\cdots,p_n\} Pn={p1,p2,⋯,pn} 和 Q m = { q 1 , q 2 , ⋯   , q m } Q_m=\{q_1,q_2,\cdots,q_m\} Qm={q1,q2,⋯,qm} 分割，由这些曲线的分割诱导的高斯链环积分的分割是一个 n × m n\times m n×m 的矩阵
G = ( L ( p 1 , q 1 ) L ( p 1 , q 2 ) ... L ( p 1 , q m ) L ( p 2 , q 1 ) L ( p 2 , q 2 ) ... L ( p 2 , q m ) ⋮ ⋮ ⋱ ⋮ L ( p n , q 1 ) L ( p n , q 2 ) ... L ( p n , q m ) ) G = \begin{pmatrix} L(p_1, q_1) & L(p_1, q_2) & \dots & L(p_1, q_m) \\ L(p_2, q_1) & L(p_2, q_2) & \dots & L(p_2, q_m) \\ \vdots & \vdots & \ddots & \vdots \\ L(p_n, q_1) & L(p_n, q_2) & \dots & L(p_n, q_m) \end{pmatrix} G= L(p1,q1)L(p2,q1)⋮L(pn,q1)L(p1,q2)L(p2,q2)⋮L(pn,q2)......⋱...L(p1,qm)L(p2,qm)⋮L(pn,qm)

定义3（尺度化高斯链环积分，Scaled Gauss linking integral）：给定有限个实数的集合 R = { r 0 , r 1 , ⋯   , r k } R=\{r_0,r_1,\cdots,r_k\} R={r0,r1,⋯,rk}，其中 0 = r 0 < r 1 < ⋯ < r k 0=r_0<r_1<\cdots<r_k 0=r0<r1<⋯<rk，则在尺度 [ r t , r t + 1 ] [r_t,r_{t+1}] [rt,rt+1] 下的高斯链环积分定义成
G r t , r t + 1 = ( χ [ r t , r t + 1 ] ( d ( p 1 , q 1 ) ) L ( p 1 , q 1 ) χ [ r t , r t + 1 ] ( d ( p 1 , q 2 ) ) L ( p 1 , q 2 ) ... χ [ r t , r t + 1 ] ( d ( p 1 , q m ) ) L ( p 1 , q m ) χ [ r t , r t + 1 ] ( d ( p 2 , q 1 ) ) L ( p 2 , q 1 ) χ [ r t , r t + 1 ] ( d ( p 2 , q 2 ) ) L ( p 2 , q 2 ) ... χ [ r t , r t + 1 ] ( d ( p 2 , q m ) ) L ( p 2 , q m ) ⋮ ⋮ ⋱ ⋮ χ [ r t , r t + 1 ] ( d ( p n , q 1 ) ) L ( p n , q 1 ) χ [ r t , r t + 1 ] ( d ( p n , q 2 ) ) L ( p n , q 2 ) ... χ [ r t , r t + 1 ] ( d ( p n , q m ) ) L ( p n , q m ) ) G^{r_t, r_{t+1}} = \begin{pmatrix} \chi_{[r_t, r_{t+1}]}\big(d(p_1, q_1)\big) L(p_1, q_1) & \chi_{[r_t, r_{t+1}]}\big(d(p_1, q_2)\big) L(p_1, q_2) & \dots & \chi_{[r_t, r_{t+1}]}\big(d(p_1, q_m)\big) L(p_1, q_m) \\ \chi_{[r_t, r_{t+1}]}\big(d(p_2, q_1)\big) L(p_2, q_1) & \chi_{[r_t, r_{t+1}]}\big(d(p_2, q_2)\big) L(p_2, q_2) & \dots & \chi_{[r_t, r_{t+1}]}\big(d(p_2, q_m)\big) L(p_2, q_m) \\ \vdots & \vdots & \ddots & \vdots \\ \chi_{[r_t, r_{t+1}]}\big(d(p_n, q_1)\big) L(p_n, q_1) & \chi_{[r_t, r_{t+1}]}\big(d(p_n, q_2)\big) L(p_n, q_2) & \dots & \chi_{[r_t, r_{t+1}]}\big(d(p_n, q_m)\big) L(p_n, q_m) \end{pmatrix} Grt,rt+1= χ[rt,rt+1](d(p1,q1))L(p1,q1)χ[rt,rt+1](d(p2,q1))L(p2,q1)⋮χ[rt,rt+1](d(pn,q1))L(pn,q1)χ[rt,rt+1](d(p1,q2))L(p1,q2)χ[rt,rt+1](d(p2,q2))L(p2,q2)⋮χ[rt,rt+1](d(pn,q2))L(pn,q2)......⋱...χ[rt,rt+1](d(p1,qm))L(p1,qm)χ[rt,rt+1](d(p2,qm))L(p2,qm)⋮χ[rt,rt+1](d(pn,qm))L(pn,qm)

其中
χ [ r t , r t + 1 ] ( x ) = { 1 , if x ∈ [ r t , r t + 1 ] 0 , else \chi_{[r_t, r_{t+1}]}(x) = \begin{cases} 1, & \text{if } x \in [r_t, r_{t+1}] \\ 0, & \text{else} \end{cases} χ[rt,rt+1](x)={1,0,if x∈[rt,rt+1]else

换句话说，它相当于是给 G G G 作用了一个"掩码"，对于那些 p i p_i pi 和 q j q_j qj 之间距离不在 [ r t , r t + 1 ] [r_t,r_{t+1}] [rt,rt+1] 范围内的坐标位置 ( i , j ) (i,j) (i,j)，把 G r t , r t + 1 ( i , j ) G^{r_t,r_{t+1}}(i,j) Grt,rt+1(i,j) 置成0，其他位置保持 G ( i , j ) G(i,j) G(i,j) 不变。可以想象， G r t , r t + 1 G^{r_t, r_{t+1}} Grt,rt+1 是一个非常稀疏的矩阵，绝大部分元素都置成0了。这一步，我们得到了 k k k 个 n × m n\times m n×m 的矩阵。

定义4（局部化尺度化高斯链环积分，Localized scaled Gauss linking integral）：对于给定尺度 [ r t , r t + 1 ] [r_t,r_{t+1}] [rt,rt+1]，定义在 p i p_i pi 或 q j q_j qj 处的局部化尺度化高斯链环积分
J r t , r t + 1 ( p i ) = ∑ s = 1 m G i s r t , r t + 1 , J r t , r t + 1 ( q j ) = ∑ s = 1 n G s j r t , r t + 1 J^{r_t,r_{t+1}}(p_i)=\sum_{s=1}^m G_{is}^{r_t,r_{t+1}},J^{r_t,r_{t+1}}(q_j)=\sum_{s=1}^n G_{sj}^{r_t,r_{t+1}} Jrt,rt+1(pi)=s=1∑mGisrt,rt+1,Jrt,rt+1(qj)=s=1∑nGsjrt,rt+1

这样，对一条曲线段 u u u，就可以把不同尺度整合起来，形成一个向量
F r a t u r e ( u ) = ( J r 1 , r 2 ( u ) , J r 2 , r 3 ( u ) , J r k − 1 , r k ( u ) ) Frature(u)=(J^{r_1,r_2}(u),J^{r_2,r_3}(u),J^{r_{k-1},r_k}(u)) Frature(u)=(Jr1,r2(u),Jr2,r3(u),Jrk−1,rk(u))

这就是我们可以得到的特征。不过，这些定义固然可以给出，但是怎么进行实际应用？如果只能应用在两条曲线，那应用范围就太过于狭窄。作者后续给出了一些例子，说明很多问题都可以化归到计算曲线之间拓扑特征的情形，这样就大大拓宽了应用范围。

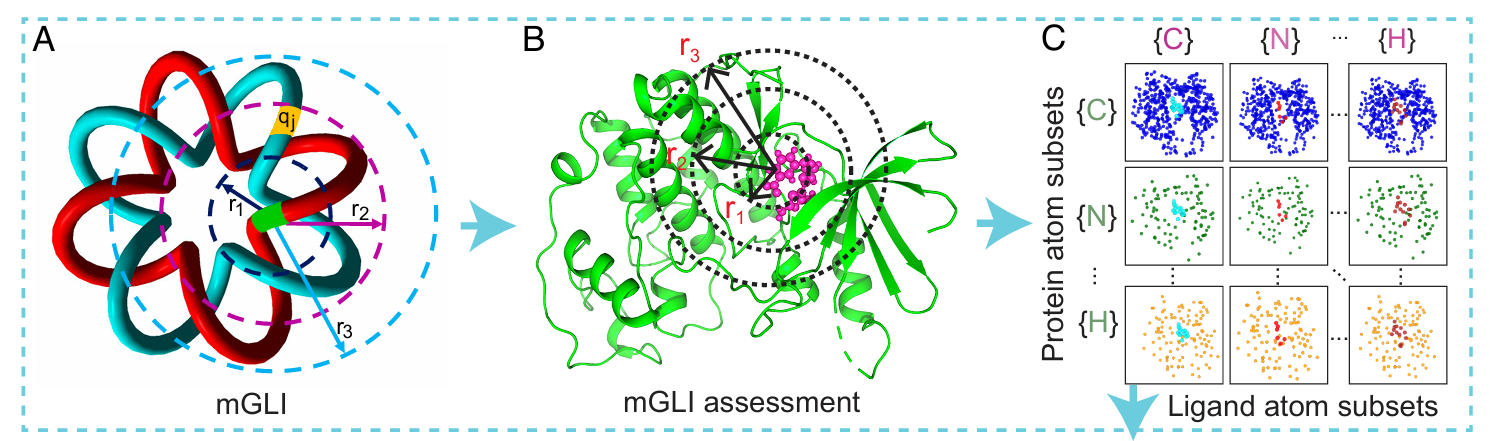
【在（A）中，考虑两个曲线段 p i p_i pi 和 q j q_j qj，知 d ( p i , q j ) ∈ [ r 1 , r 2 ] d(p_i,q_j)\in [r_1,r_2] d(pi,qj)∈[r1,r2]，因此， χ [ r 1 , r 2 ] ( d ( p i , q j ) ) = 1 \chi_{[r_1, r_2]}(d(p_i,q_j)) =1 χ[r1,r2](d(pi,qj))=1，余下都是0；从而 G i j r 1 , r 2 = χ [ r 1 , r 2 ] ( d ( p i , q j ) ) L ( p i , q j ) = L ( p i , q j ) G_{ij}^{r_1,r_2}=\chi_{[r_1, r_2]}(d(p_i,q_j))L(p_i,q_j)=L(p_i,q_j) Gijr1,r2=χ[r1,r2](d(pi,qj))L(pi,qj)=L(pi,qj)，余下都是0。】
二、应用

首先将高斯链环积分进行推广。对于任何可分割为曲线段 P n P_n Pn 和 Q m Q_m Qm 的拓扑或几何结构，均可定义如下分割矩阵：
G ‾ = ( g ( p 1 , q 1 ) g ( p 1 , q 2 ) ... g ( p 1 , q m ) g ( p 2 , q 1 ) g ( p 2 , q 2 ) ... g ( p 2 , q m ) ⋮ ⋮ ⋱ ⋮ g ( p n , q 1 ) g ( p n , q 2 ) ... g ( p n , q m ) ) \overline{G} = \begin{pmatrix} g(p_1, q_1) & g(p_1, q_2) & \dots & g(p_1, q_m) \\ g(p_2, q_1) & g(p_2, q_2) & \dots & g(p_2, q_m) \\ \vdots & \vdots & \ddots & \vdots \\ g(p_n, q_1) & g(p_n, q_2) & \dots & g(p_n, q_m) \end{pmatrix} G= g(p1,q1)g(p2,q1)⋮g(pn,q1)g(p1,q2)g(p2,q2)⋮g(pn,q2)......⋱...g(p1,qm)g(p2,qm)⋮g(pn,qm)

其中，矩阵元素 g ( p i , q j ) g(p_i,q_j) g(pi,qj) 的定义为：
g ( p i , q j ) = { L ( p i , q j ) 若 p i ∩ q j 为空集 , 0 其他情况 . g(p_i, q_j) = \begin{cases} L(p_i, q_j) & \text{若 } p_i \cap q_j \text{ 为空集}, \\ 0 & \text{其他情况}. \end{cases} g(pi,qj)={L(pi,qj)0若 pi∩qj 为空集,其他情况.

这里 P n P_n Pn 和 Q m Q_m Qm 中的曲线片段允许相交甚至重合。
A.描述蛋白质分子多肽链

我们将蛋白质视为开放曲线，认为蛋白质分子的多肽链可看作一个开放多边形 l l l，其顶点对应 C α C_\alpha Cα 原子，边代表连接相邻氨基酸残基中 C α C_\alpha Cα 原子的伪键（pseudobond）。这样，我们可以诱导出若干曲线：
p i = { x ∈ l ∣ f ( x , c i ) = i n f c ∈ C f ( x , c ) } , 1 ≤ i ≤ n p_i=\{x\in l|f(x,c_i)=inf_{c\in C}f(x,c)\},1\leq i\leq n pi={x∈l∣f(x,ci)=infc∈Cf(x,c)},1≤i≤n

其中 f ( a , b ) f(a,b) f(a,b) 为点 a a a 和点 b b b 沿曲线 l l l 的距离， c i c_i ci 为 C α C_\alpha Cα 原子的三维坐标， C C C 为 C α C_\alpha Cα 原子的集合。通俗地说， p i p_i pi 是一条曲线，它由一些点构成，这些点到坐标为 r i r_i ri 的原子的距离比到其他所有原子的距离都近。这里的"距离"指的是沿曲线行走的距离。

另外，我们可定义 d ( p i , q j ) = d E ( r i , r j ) d(p_i,q_j)=d_E(r_i,r_j) d(pi,qj)=dE(ri,rj) 就是三维空间中的欧式距离。这样，我们就得到了用于研究蛋白质片段间交叉情况的高斯链环积分的分割：
G = ( L ( p 1 , p 1 ) L ( p 1 , p 2 ) ... L ( p 1 , p n ) L ( p 2 , p 1 ) L ( p 2 , p 2 ) ... L ( p 2 , p n ) ⋮ ⋮ ⋱ ⋮ L ( p n , p 1 ) L ( p n , p 2 ) ... L ( p n , p n ) ) = ( 0 L ( p 1 , p 2 ) ... L ( p 1 , p n ) L ( p 2 , p 1 ) 0 ... L ( p 2 , p n ) ⋮ ⋮ ⋱ ⋮ L ( p n , p 1 ) L ( p n , p 2 ) ... 0 ) G = \begin{pmatrix} L(p_1, p_1) & L(p_1, p_2) & \dots & L(p_1, p_n) \\ L(p_2, p_1) & L(p_2, p_2) & \dots & L(p_2, p_n) \\ \vdots & \vdots & \ddots & \vdots \\ L(p_n, p_1) & L(p_n, p_2) & \dots & L(p_n, p_n) \end{pmatrix} = \begin{pmatrix} 0 & L(p_1, p_2) & \dots & L(p_1, p_n) \\ L(p_2, p_1) & 0 & \dots & L(p_2, p_n) \\ \vdots & \vdots & \ddots & \vdots \\ L(p_n, p_1) & L(p_n, p_2) & \dots & 0 \end{pmatrix} G= L(p1,p1)L(p2,p1)⋮L(pn,p1)L(p1,p2)L(p2,p2)⋮L(pn,p2)......⋱...L(p1,pn)L(p2,pn)⋮L(pn,pn) = 0L(p2,p1)⋮L(pn,p1)L(p1,p2)0⋮L(pn,p2)......⋱...L(p1,pn)L(p2,pn)⋮0

对于参数 r r r，让它从 5Å 开始，延伸至 17Å，每个尺度区间为 1Å。即，
r 1 = 5 A ˚ , r 2 = 6 A ˚ , ⋯   , r 13 = 17 A ˚ r_1=5Å, r_2=6Å, \cdots, r_{13}=17Å r1=5A˚,r2=6A˚,⋯,r13=17A˚

这样就可以计算前文提到的 F e a t u r e ( u ) Feature(u) Feature(u) 了。
B.描述蛋白质 - 配体复合物的特征

蛋白质或配体分子中的每个原子 c i c_i ci 通过多个共价键与相邻原子连接，形成原子 c i c_i ci 特有的曲线分割。这些曲线段以中心原子为起点，延伸至相关共价键的中点，最终形成原子特异性曲线分割：
p i = { x ∈ l ∣ f ( x , c i ) ≤ 1 2 f ( c , c i ) , c ∈ C } p_i=\{x\in l|f(x,c_i)\leq \frac{1}{2}f(c,c_i),c\in C\} pi={x∈l∣f(x,ci)≤21f(c,ci),c∈C}

其中 C C C 为通过共价键与原子 c i c_i ci 连接的相邻原子集合， l l l 表示每条共价键代表的直线。

假设蛋白质中关注四种原子（C、N、O、S），配体中考虑十种原子（C、N、O、H、S、P、F、Cl、Br、I）。设 P n C P_n^C PnC 和 Q m N Q_m^N QmN 分别表示蛋白质中碳（C）原子特异性曲线分割集合和配体中氮（N）原子特异性曲线分割集合，即
P n C = { p 1 C , p 2 C , ⋯   , p n C } , Q m N = { p 1 N , p 2 N , ⋯   , p m N } P_n^C=\{p_1^C,p_2^C,\cdots,p_n^C\},Q_m^N=\{p_1^N,p_2^N,\cdots,p_m^N\} PnC={p1C,p2C,⋯,pnC},QmN={p1N,p2N,⋯,pmN}

完全类似地，我们可以计算 L ( p i C , q j N ) L(p_i^C,q_j^N) L(piC,qjN)（称为 a-GLI，即 atom-by-atom Gauss linking integrals）。注意这里由于一个原子可能对应多个曲线段，会产生多个积分结果，不能直接用单一数值代表，需要用统计量汇总，作者选取中位数和标准差这两个统计量表征 L ( p i C , q j N ) L(p_i^C,q_j^N) L(piC,qjN)。

仍取欧式距离 d ( p i C , q j N ) = d E ( r i C , r j N ) d(p_i^C,q_j^N)=d_E(r_i^C,r_j^N) d(piC,qjN)=dE(riC,rjN)，这样就可以计算 G r t , r t + 1 G^{r_t, r_{t+1}} Grt,rt+1，从而得到 J r t , r t + 1 ( p i C , q m N ) J^{r_t,r_{t+1}}(p_i^C,q_m^N) Jrt,rt+1(piC,qmN)（遍历 i = 1 , 2 , ⋯   , n i=1,2,\cdots,n i=1,2,⋯,n） 和 J r t , r t + 1 ( p n C , q j N ) J^{r_t,r_{t+1}}(p_n^C,q_j^N) Jrt,rt+1(pnC,qjN)（遍历 j = 1 , 2 , ⋯   , m j=1,2,\cdots,m j=1,2,⋯,m），再通过以下公式利用统计量确定多尺度元素特异性高斯链环积分（e-GLI）：
J r t , r t + 1 ( P n C , Q m N ) = 统计量 of { J r t , r t + 1 ( p 1 C , Q m N ) , J r t , r t + 1 ( p 2 C , Q m N ) , ... , J r t , r t + 1 ( p n C , Q m N ) } J^{r_t, r_{t+1}}\left(P_n^C, Q_m^N\right) = \text{统计量 of } \left\{ J^{r_t, r_{t+1}}\left(p_1^C, Q_m^N\right), J^{r_t, r_{t+1}}\left(p_2^C, Q_m^N\right), \dots, J^{r_t, r_{t+1}}\left(p_n^C, Q_m^N\right) \right\} Jrt,rt+1(PnC,QmN)=统计量 of {Jrt,rt+1(p1C,QmN),Jrt,rt+1(p2C,QmN),...,Jrt,rt+1(pnC,QmN)}
J r t , r t + 1 ( Q m N , P n C ) = 统计量 of { J r t , r t + 1 ( q 1 N , P n C ) , J r t , r t + 1 ( q 2 N , P n C ) , ... , J r t , r t + 1 ( q m N , P n C ) } J^{r_t, r_{t+1}}\left(Q_m^N, P_n^C\right) = \text{统计量 of } \left\{ J^{r_t, r_{t+1}}\left(q_1^N, P_n^C\right), J^{r_t, r_{t+1}}\left(q_2^N, P_n^C\right), \dots, J^{r_t, r_{t+1}}\left(q_m^N, P_n^C\right) \right\} Jrt,rt+1(QmN,PnC)=统计量 of {Jrt,rt+1(q1N,PnC),Jrt,rt+1(q2N,PnC),...,Jrt,rt+1(qmN,PnC)}

我们将这种方法称为 mGLI-bin 特征化。也可将尺度区间的起点延伸至 0，得到以下公式：
J 0 , r t + 1 ( P n C , Q m N ) = 统计量 of { J 0 , r t + 1 ( p 1 C , Q m N ) , J 0 , r t + 1 ( p 2 C , Q m N ) , ... , J 0 , r t + 1 ( p n C , Q m N ) } J^{0, r_{t+1}}\left(P_n^C, Q_m^N\right) = \text{统计量 of } \left\{ J^{0, r_{t+1}}\left(p_1^C, Q_m^N\right), J^{0, r_{t+1}}\left(p_2^C, Q_m^N\right), \dots, J^{0, r_{t+1}}\left(p_n^C, Q_m^N\right) \right\} J0,rt+1(PnC,QmN)=统计量 of {J0,rt+1(p1C,QmN),J0,rt+1(p2C,QmN),...,J0,rt+1(pnC,QmN)}
J 0 , r t + 1 ( Q m N , P n C ) = 统计量 of { J 0 , r t + 1 ( q 1 N , P n C ) , J 0 , r t + 1 ( q 2 N , P n C ) , ... , J 0 , r t + 1 ( q m N , P n C ) } J^{0, r_{t+1}}\left(Q_m^N, P_n^C\right) = \text{统计量 of } \left\{ J^{0, r_{t+1}}\left(q_1^N, P_n^C\right), J^{0, r_{t+1}}\left(q_2^N, P_n^C\right), \dots, J^{0, r_{t+1}}\left(q_m^N, P_n^C\right) \right\} J0,rt+1(QmN,PnC)=统计量 of {J0,rt+1(q1N,PnC),J0,rt+1(q2N,PnC),...,J0,rt+1(qmN,PnC)}

我们将这种方法称为 mGLI-all 特征化。在蛋白质 - 配体复合物表征中，定义尺度半径集合
R = { 0 , 2 A ˚ , 3 A ˚ , ⋯   , 12 A ˚ } R=\{0,2Å,3Å,\cdots,12Å\} R={0,2A˚,3A˚,⋯,12A˚}

那么每种特征化方法均生成一个长度为 8800 的 mGLI 特征向量，计算方式为：4（蛋白质原子种类）×10（配体原子种类）×2（两种e-GLI）×11（尺度数量）×5（e-GLI 的统计量）×2（a-GLI 的统计量）=8800。这里e-GLI 的统计量包括求和、最小值、最大值、平均值和中位数共5种，a-GLI 的统计量就是刚提到的用中位数和标准差这两个统计量表征 L ( p i C , q j N ) L(p_i^C,q_j^N) L(piC,qjN)。作者通过实验论证了这些特征在蛋白质分析中的效果。

我自己也读了一些持续同调相关的文章了，像这种能提出一套新颖的 filtration（在我看来KDA就是TDA的变体，划分尺度区间 [ r i , r i + 1 ] [r_i,r_{i+1}] [ri,ri+1] 就像构建 filtration），并且给出应用的工作算是很好的工作了，很多工作都只是运用常见的 Vietoris--Rips 复形等进行数据分析。当然，运用通常构造的 filtration，能够挖掘一些关联（比如分子结构与材料功能之间的关联等等），并给出在对应领域的实际应用，也是有意义的工作。持续同调仍然是大有可为的一个方向。