Metric3D Towards Zero-shot Metric 3D Prediction from A Single Image 论文学习

代码地址：https://github.com/YvanYin/Metric3D

解决了什么问题？

3D重建是自动驾驶、机器人等领域的核心技术。从图像中重建出准确的 3D 场景是一个长久以来存在的视觉任务。由于单张图片恢复3D信息是不适定问题（ill-posed），主流的成熟方法通常需要多视角几何（multi-view geometry），这就无法应用于仅有单张图片的场景，因为它们需要先验信息才能进行三维重建。当前单目深度估计的方法有两类局限：

只能针对单一的相机模型训练，无法混合不同的数据训练（因为不同的相机有不同的内参和尺度，导致尺度模糊性和 metric ambiguity），它们无法泛化到未见过的相机或场景。
另一种方法（如 MiDas、LeReS 和 HDN ）虽然用大规模混合数据训练，实现了较好的零样本泛化（zero-shot generalization），但学的是仿射不变深度（affine-invariant depth），其深度仅在未知的偏移或缩放尺度下是准确的，无法恢复真实世界的绝对尺度（metric scale）。

作者认为，要实现零样本、单视图、绝对尺度的深度估计，关键要解决两个问题：

大规模数据训练。
解决不同相机模型带来的尺度模糊性。

于是作者提出了一个"规范相机空间变换模块"，可以：

显式解决不同相机之间的尺度/内参模糊问题。
可轻易地插入现有的单目深度估计模型。
让模型能够用超过800万张图片、上千种相机模型进行稳定的训练，从而对未知相机拍摄的图片实现零样本泛化。

实验结果表明，本方法在7个零样本基准测试中达到SOTA（当前最优）性能。它可以做到：

从任意的网络图片中恢复精确的绝对尺度3D结构，使得"单张图片进行测量"成为可能。
提升下游任务性能，例如：显著缓解单目SLAM中的尺度漂移问题，实现高质量、绝对尺度的稠密地图构建。

根据预测深度的类型，现有的方法可以分为三种：学习度量深度、学习相对深度、学习仿射不变深度。尽管度量深度在各基准测试中效果不错，但它们需要在相同的相机内参的数据集上进行训练和测试。因此，度量深度方法的训练数据集通常较小，很难用同一台相机收集多样化场景的大规模数据集。后果就是，这些模型缺乏可迁移性，对真实世界的图像泛化能力就很差。另一种折中的方法就是学习相对深度，它只表示一个点比另一个点更远或更近，相对深度的应用很有限。学习仿射不变深度是上述两类方法之间的一个折中。通过使用大规模数据，它们在训练过程中解耦了度量信息，从而实现了出色的鲁棒性和泛化能力。目前最先进的 LeReS 可以恢复真实世界的三维场景，但仅能恢复到未知的尺度和偏移。

本文主要关注在零样本、可迁移、度量深度估计这一目标上。首先，作者分析了单目深度估计的度量模糊性问题，研究了不同相机参数，包括像素大小、焦距和传感器大小。作者认为，焦距是恢复深度的关键因素，需要一种不依赖有限相机类型、且能显式处理焦距变化的方法。

LeReS 在训练时忽略了焦距信息，导致模型在遇到不同焦距的图片时，无法确定其绝对尺度，因此只能放弃度量信息，输出仿射不变深度。
另一类方法如 CamConv 尝试将相机模型编码到网络中，让网络从图片外观中隐式地理解相机参数，但这种方法严重受限于训练数据中相机类型的数量和多样性，网络容量有限，难以泛化到无数种未知的相机。

作者从人体姿态重建领域获得灵感，

人体姿态重建：为了处理无数种人体姿态，研究者将所有样本映射到一个规范姿态空间（如"T-pose"）进行训练，以减少姿态差异。
本文思路：为了处理无数种相机，我们将所有训练数据映射到一个规范相机空间。经过变换后，所有图片都被粗略地视为由同一台"规范相机"拍摄。

那么如何实现这种变换？作者提出了两种在训练时使用的并行方法，

调整图片外观：通过图像处理技术（如模拟不同的焦距效果），将原始图片"变换"成由规范相机拍摄的样子。
变换真值标签：保持原始图片不变，但根据原始相机与规范相机之间的参数差异，相应地变换深度图的真值标签，使其与规范相机匹配。

这样做，相机模型没有被编码进网络。网络永远只学习"规范相机"这一种成像模式。这使得该方法可以轻松即插即用到任何现有的深度估计网络架构中。在进行预测时，只需对网络的输出（在规范相机空间下的深度）做一个逆变换，即可恢复出原始图片对应的真实度量深度。

为了解决仿射不变深度方法中，全局归一化损失会弱化局部细节的问题，作者提出了一个新的损失函数 --- 随机区域归一化损失。这个损失函数迫使网络不仅关注图片的全局几何结构，还要精确地学习每个局部区域的深度细节和分布，从而显著提升深度图的局部精度和细腻程度。

旧方法（尺度-偏移不变损失）：在整张图片上进行全局归一化。这虽然强调了整体深度分布，但会"压扁"细微的深度差异（例如物体表面的纹理起伏）。
随机区域归一化损失：从图片中随机裁剪多个小图块，在每个图块上，独立地使用尺度-偏移不变损失。

意义

大规模训练和卓越性能：通过本文方法，我们可以轻松地将模型训练扩展到来自11个数据集的800万张图像。之前的方法因为无法混合不同相机数据，数据集规模受限。而本文的规范相机空间变换模块解决了相机差异，使得用海量、多源、多相机数据训练成为可能。
实现单图像测量学：仅凭一张照片，就能进行真实的物理测量（如估算物体的长度、高度、面积）。本文首次让基于学习的方法、在无需已知相机参数的前提下、可靠地实现这一目标成为可能。
赋能下游任务：超越仿射不变模型，仿射不变深度缺少尺度，像SLAM、3D重建等需要精确尺度的任务无法直接使用。单目SLAM在长距离运行时，会产生严重的尺度漂移（估计的地图整体被放大或缩小）。将本文预测的度量深度作为强约束引入SLAM系统，能显著降低尺度漂移，从而得到更高质量、具有真实世界度量尺度的地图。

方法

前提

本文使用的小孔成像相机模型的内参包含了： [ [ f ^ / δ , 0 , u 0 ] , [ 0 , f ^ / δ , v 0 ] , [ 0 , 0 , 1 ] ] [[\hat{f}/\delta, 0, u_0], [0, \hat{f}/\delta, v_0], [0,0,1]] [[f^/δ,0,u0],[0,f^/δ,v0],[0,0,1]]，其中 f ^ \hat{f} f^是焦距（微米）， δ \delta δ是单个像素的物理尺寸（微米）， ( u 0 , v 0 ) (u_0, v_0) (u0,v0)是相机主点。 f = f ^ / δ f=\hat{f}/\delta f=f^/δ 是用像素个数表示的焦距值。

度量模糊性分析

下图是不同相机在不同距离拍摄的图片。仅从图像的外观来看，人们可能认为最后两张图片是在接近的位置用同一个相机拍摄的。实际上，由于焦距不同，这些图片是在不同的位置拍摄的。因此，对于从单张图片估计度量距离来说，相机内参非常关键。为了避免度量模糊性，MiDaS 和 LeReS 从监督信号中解耦了度量，妥协地去学习仿射不变的深度。

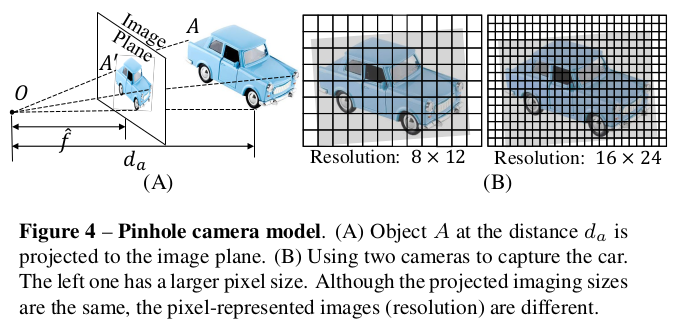
下图A 展示了一个简单的小孔透视投影。位于 d a d_a da的物体 A A A投影到 A ′ A' A′。根据相似性原理，我们可以得到等式

d a = S ^ [ f ^ S ^ ′ ] = S ^ ⋅ α d_a = \hat{S}[\frac{\hat{f}}{\hat{S}'}]=\hat{S}\cdot \alpha da=S^[S^′f^]=S^⋅α

其中 S ^ \hat{S} S^和 S ^ ′ \hat{S}' S^′是真实和投影后的大小。 ⋅ ^ \hat{\cdot} ⋅^表示它的单位是物理尺寸（微米）。为了从单张图片恢复 d a d_a da，必须要有焦距、真实世界的物体大小和物体在图像上的大小。从单张图片估计焦距是非常有挑战性且不适定的问题。目前的方法都不是很令人满意。这里作者假设训练/测试图像的焦距是已知的，来简化问题。相比之下，理解成像尺寸（物体在图片上占多少个像素）对神经网络来说要容易得多。神经网络（特别是卷积神经网络）是天生的图像处理专家，它非常擅长从像素分布中识别物体的大小、形状和相对位置。这是它的"本职工作"。为了获得物体的真实世界尺寸，神经网络需要理解语义场景布局和物体本身，而这正是神经网络所擅长的。作者定义了 α = f ^ / S ^ ′ \alpha=\hat{f}/\hat{S}' α=f^/S^′，因此 d a d_a da与 α \alpha α是正比关系。恢复真实尺寸是一个"三角测量"问题：你需要结合两个信息：

角度信息：由焦距决定，物体在相机视角中张开了多大的角度，焦距是网络难以直接从图片外观中精确学习得到的。
像素尺寸信息：这个角度在图片上对应了多少像素？这由物体的真实大小和距离共同决定。网络可以凭其强大的语义理解能力来判断：这是一辆"汽车"（已知真实尺寸大概为4-5米长）还是一个"杯子"（已知大概0.1米高）。

关于传感器尺寸、像素尺寸和焦距，作者由如下发现。

O1: 在针孔相机模型中，影响单目度量深度估计的关键相机参数是焦距，而传感器尺寸和像素尺寸并不直接影响深度估计 。根据透视投影，传感器大小只会影响视场角（FoV），传感器越大，在相同焦距下，能捕捉到的场景范围（FOV）越宽。 d a S ^ = f ^ S ^ ′ \frac{d_a}{\hat{S}} = \frac{\hat{f}}{\hat{S}'} S^da=S^′f^ 这个公式是关键，因此传感器大小和 α \alpha α无关，就不会影响度量深度估计。对于像素尺寸，我们假设由两个像素尺寸（ δ 1 = 2 δ 2 \delta_1=2\delta_2 δ1=2δ2）不同而焦距相同 f ^ \hat{f} f^的相机模型，在 d a d_a da距离拍摄同一个物体。下图B展示了它们拍摄的图片。如前所述，像素个数表示的焦距值 f 1 = 1 2 f 2 f_1 = \frac{1}{2}f_2 f1=21f2。由于第二个相机的像素尺寸更小，尽管它们在图像上的投影大小都是 S ^ ′ \hat{S}' S^′，但像素个数表示的图像分辨率是 S 1 ′ = 1 2 S 2 ′ S'_1 = \frac{1}{2}S'_2 S1′=21S2′。根据等式1， f ^ δ 1 ⋅ S 1 ′ = f ^ δ 2 ⋅ S 2 ′ \frac{\hat{f}}{\delta_1 \cdot S'_1} = \frac{\hat{f}}{\delta_2 \cdot S'_2} δ1⋅S1′f^=δ2⋅S2′f^，即 α 1 = α 2 \alpha_1 = \alpha_2 α1=α2，所以由 d 1 = d 2 d_1 = d_2 d1=d2。因此，不同的相机传感器不会影响度量深度估计。

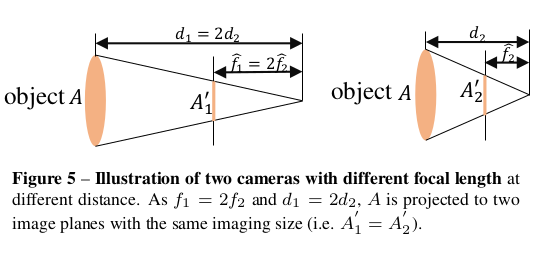
O2：焦距对于度量深度估计非常重要 。图3展示了由于焦距未知而导致的度量模糊性问题。下图也说明了这点。如果两个不同的相机（ f ^ 1 = 2 f ^ 2 \hat{f}_1 = 2\hat{f}_2 f^1=2f^2）在不同的距离 d 1 = 2 d 2 d_1 = 2d_2 d1=2d2，投影图像尺寸却是一样的。因此，只从外观来看，当监督信号不同时，网络会非常迷惑。于是作者提出了一个规范相机变换方法，解决监督信号和图像外观冲突的问题。

规范相机变换

这儿的核心思想就是设定一个规范的相机空间 ( ( f x c , f y c ) , f x c = f y c = f c ) ((f_x^c, f_y^c), f_x^c=f_y^c=f^c) ((fxc,fyc),fxc=fyc=fc)，然后将所有的训练数据都变换到此空间。因此，所有的数据都可以当作是通过规范相机拍摄的。作者提出了两种变换方法，要么变换输入图像 I ∈ R H × W × 3 \mathbf{I}\in \mathbb{R}^{H\times W\times 3} I∈RH×W×3，要么变换真实标签 D ∈ R H × W \mathbf{D}\in \mathbb{R}^{H\times W} D∈RH×W。原始的内参是 { f , u 0 , v 0 } \{f,u_0,v_0\} {f,u0,v0}。

方法1：变换深度标签

第一个方法是直接变换真实深度标签来解决这个问题。在训练时，将真实深度 D ∗ \mathbf{D}^\ast D∗ 通过比值 ω d = f c f \omega_d = \frac{f^c}{f} ωd=ffc来缩放，即 D c ∗ = ω d D ∗ \mathbf{D}^\ast_c = \omega_d \mathbf{D}^\ast Dc∗=ωdD∗。推理时，预测深度 D c \mathbf{D}_c Dc是在规范空间，需要进行逆变换来恢复度量信息，即 D = 1 ω d D c \mathbf{D} = \frac{1}{\omega_d} \mathbf{D}_c D=ωd1Dc。注意，输入图像 I \mathbf{I} I不用做任何的变换，即 I c = I \mathbf{I}_c=\mathbf{I} Ic=I。

方法2：变换输入图像

从另一个视角来看，模糊性也可以认为是相似图像外观造成的。因此可以通过变换输入图像来模拟规范相机拍摄的效果。将输入图像 I \mathbf{I} I通过系数 ω r = f c f \omega_r=\frac{f^c}{f} ωr=ffc缩放，即 I c = T ( I , ω r ) \mathbf{I}_c=\mathcal{T}(\mathbf{I}, \omega_r) Ic=T(I,ωr)，其中 T \mathcal{T} T表示图像缩放。光学中心也被缩放了，因此规范相机模型就是 { f c , ω r u 0 , ω r v 0 } \{f^c, \omega_r u_0, \omega_r v_0\} {fc,ωru0,ωrv0}。真实标签会进行无缩放的重置大小操作，即 D c ∗ = T ( D ∗ , ω r ) \mathbf{D}^\ast_c = \mathcal{T}(\mathbf{D}^\ast, \omega_r) Dc∗=T(D∗,ωr)，他们只改变图片的尺寸（像素矩阵的行列数），但不改变深度图中每个像素所代表的真实物理深度值。推理时，逆变换将预测结果缩放到原始尺寸，即 D = T ( D c , 1 ω r ) \mathbf{D}=\mathcal{T}(\mathbf{D}_c, \frac{1}{\omega_r}) D=T(Dc,ωr1)。

下图展示了这个流程。变换完成后，随机裁剪图块用于训练。裁剪操作只调整 FOV 和光学中心，不会造成任何度量模糊性问题。在标签变换方法中， ω r = 1 , ω d = f c f \omega_r=1, \omega_d=\frac{f^c}{f} ωr=1,ωd=ffc，而在图像变换方法中 ω d = 1 , ω r = f c f \omega_d=1, \omega_r=\frac{f^c}{f} ωd=1,ωr=ffc。训练的目标是

min ⁡ θ ∣ N d ( I c , θ ) − D c ∗ ∣ \min_\theta |\mathcal{N}_d(\mathbf{I}_c, \theta) - \mathbf{D}^\ast_c| θmin∣Nd(Ic,θ)−Dc∗∣

其中 θ \theta θ是网络 N d \mathcal{N}_d Nd的参数。 D c ∗ \mathbf{D}^\ast_c Dc∗和 I c \mathbf{I}_c Ic是变换后的真实深度标签和图像。

混合数据训练是提升模型泛化能力的有效途径。作者收集了11个不同的数据集进行混合训练。这确保了数据在场景类型（如室内、室外、城市、自然）、物体类别和视觉外观上具有极高的多样性，让模型能学到通用的3D结构先验，而非特定数据集的特征。数据中包含了超过10,000种不同的相机（如各种型号的手机、数码相机、行车记录仪等）。所有收集的数据必须包含配对的相机内参，这是本文提出的规范相机空间变换模块所需的必要条件。

监督损失

为了进一步提升表现，作者提出了一个随机区域归一化损失。目前主流的、用于训练仿射不变深度模型（如MiDaS, LeReS）的尺度-偏移不变损失具有以下的局限性：

原理：对整张图片的深度预测值和真值，分别计算中位数和绝对中位差，然后进行归一化，使得两者的尺度和偏移一致。这样做可以"解耦"绝对尺度，让网络专注于学习图片内部的相对深度结构。
缺点：这种全局归一化会"压平"图片中细粒度的深度差异。具体来说，在那些距离相机很近的区域，物体表面的起伏、褶皱、小结构之间的微小深度差别，在整张图的全局统计量对比下变得不再明显，导致网络在训练时对这些局部细节的学习动力不足，预测结果容易显得"平滑"而缺乏精细的几何纹理。

为了解决上述问题，作者提出了一种"分而治之" 的策略：

随机裁剪：在训练时，从规范相机空间下的深度图真值 D c ∗ \mathbf{D}^\ast_c Dc∗ 和预测的深度图 D c \mathbf{D}c Dc 中随机裁剪出多个小块， p i ( i = 0 , . . . , M ) ∈ R h i × w i p{i(i=0,...,M)} \in \mathbb{R}^{h_i\times w_i} pi(i=0,...,M)∈Rhi×wi。
局部归一化：对于每一对裁剪出的真值小块和预测小块，独立地应用中位数绝对偏差归一化。这个操作具体是：
- 计算小块内深度值的中位数和绝对中位差。
- 用这个局部统计量对该小块进行归一化。
计算损失：在这些归一化后的小块对上，计算损失函数（如L1或L2损失），然后对所有小块损失求平均。

损失函数如下：

L R P N L = 1 M N ∑ p i M ∑ j N ∣ d p i , j ∗ − μ ( d p i , j ∗ ) 1 N ∑ j N ∣ d p i , j ∗ − μ ( d p i , j ∗ ) ∣ − d p i , j − μ ( d p i , j ) 1 N ∑ j N ∣ d p i , j − μ ( d p i , j ) ∣ ∣ L_{RPNL}=\frac{1}{MN}\sum_{p_i}^M \sum_{j}^N |\frac{d^\ast_{p_i,j} - \mu(d^\ast_{p_i,j})}{\frac{1}{N}\sum_j^N |d^\ast_{p_i,j} - \mu(d^\ast_{p_{i},j})|} - \frac{d_{p_i,j} - \mu(d_{p_i,j})}{\frac{1}{N}\sum_j^N |d_{p_i,j} - \mu(d_{p_{i},j})|}| LRPNL=MN1pi∑Mj∑N∣N1∑jN∣dpi,j∗−μ(dpi,j∗)∣dpi,j∗−μ(dpi,j∗)−N1∑jN∣dpi,j−μ(dpi,j)∣dpi,j−μ(dpi,j)∣

这里 d ∗ ∈ D c ∗ d^\ast \in \mathbf{D}^\ast_c d∗∈Dc∗是真实深度， d ∈ D c d \in \mathbf{D}c d∈Dc 是预测深度。 μ ( ⋅ ) \mu(\cdot) μ(⋅)是深度的中位数。 M M M是候选裁剪区域的个数，设为 32。训练时，从图像中随机裁剪候选区域，大小是原图尺寸的 0.125 0.125 0.125 到 0.5 0.5 0.5。此外，也用了其它的几项损失，包括了缩放无关的对数损失 L s i l o g L{silog} Lsilog、对范数回归损失 L P W N L_{PWN} LPWN、虚拟范数损失 L V N L L_{VNL} LVNL。注意 L s i l o g L_{silog} Lsilog 是 L1 损失的变种。整体损失如下：

L = L P W N + L V N L + L s i l o g + L R P N L L=L_{PWN}+L_{VNL}+L_{silog}+L_{RPNL} L=LPWN+LVNL+Lsilog+LRPNL

Metric3D Towards Zero-shot Metric 3D Prediction from A Single Image 论文学习

解决了什么问题？

意义

相关工作

单图像三维重建

有监督的单目深度估计

大规模数据训练

方法

前提

度量模糊性分析

规范相机变换

方法1：变换深度标签

方法2：变换输入图像

监督损失