Scikit-learn python的一个针对机器学习的算法库,不支持深度学习和强化学习。
=======================================================
基于单因素的线性回归模型
练习目的:
基于generated_data.csv中的数据x,y,建立线性模型,并预测当输入是3.5时的预测值
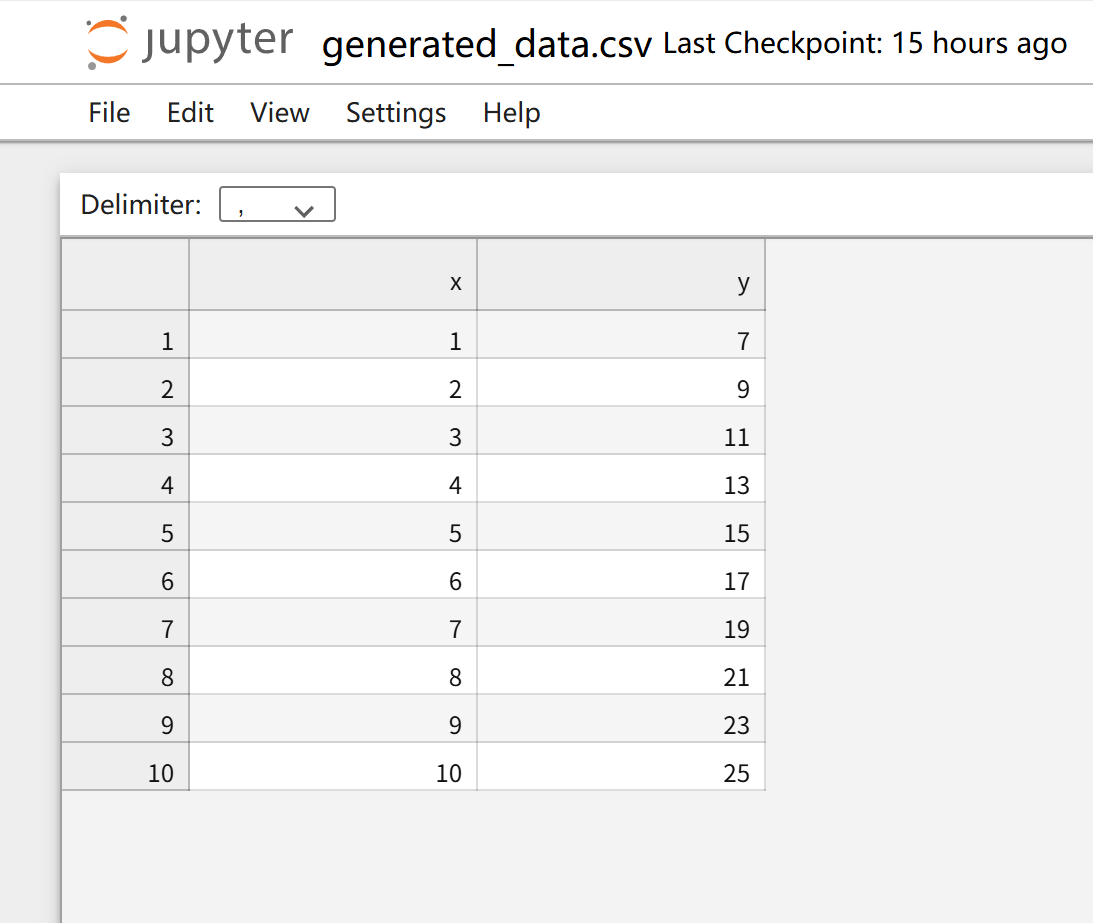
import pandas as pd
data = pd.read_csv('generated_data.csv') #引入数据
#分别获取x,y的值
x = data.loc[:,'x']
y = data.loc[:,'y']
#展示图形
import matplotlib
from matplotlib import pyplot as plt
plt.figure
plt.scatter(x,y)
plt.show()
#set linear regression model 设置线性模型
import sklearn
from sklearn.linear_model import LinearRegressionlr_model = LinearRegression()
import numpy as np #数据格式处理,LinearRegression只能处理多维数组
x = np.array(x) #转为数组
print(type(x),x.shape)
x = x.reshape(-1,1) #转为10行,1列的数组,虽然我也没咋理解为啥这样写能让一个(10,)格式的数组变成一个(10,1)的数组。转为多维数组
print(type(x),x.shape)
y = np.array(y)
print(type(y),y.shape)
y = y.reshape(-1,1)
print(type(y),y.shape)
lr_model.fit(x,y) #把输入与输出投入训练
#预测x是3.5时的值
y_3 = lr_model.predict([[3.5]])
print(y_3)
predict_y = lr_model.predict(x)
print(predict_y)
#打印系数a和截距b
a = lr_model.coef_
b = lr_model.intercept_
print(a,b)
模型训练好坏的评估指标

from sklearn.metrics import mean_squared_error,r2_score
MSE = mean_squared_error(y,predict_y)
R2 = r2_score(y,predict_y)
print(MSE,R2)
plt.figure()
plt.scatter(y,predict_y)
plt.show()
plt.figure()
plt.plot(y,predict_y)
plt.show()
====================================================================
基于多因素的线性回归模型
练习目的:
通过房屋人员的收入、房龄、房间数、受欢迎程度、房屋面积,预测房屋价格。
'''
基于usa_housing_price.csv数据,建立线性回归模型,预测合理房价:
1、以面积为输入变量,建立单因子模型,评估模型表现,可视化线性回归预测结果
2、以income、house age、numbers of rooms、population、area为输入变量,建立多因子模型,评估模型表现
3、预测
Income=65000, House Age=5, Number of Rooms=5, Population=30000, size=200的合理房价
'''
import pandas as pd
import numpy as np
data = pd.read_csv('usa_housing_price.csv')
data.head()
from matplotlib import pyplot as plt
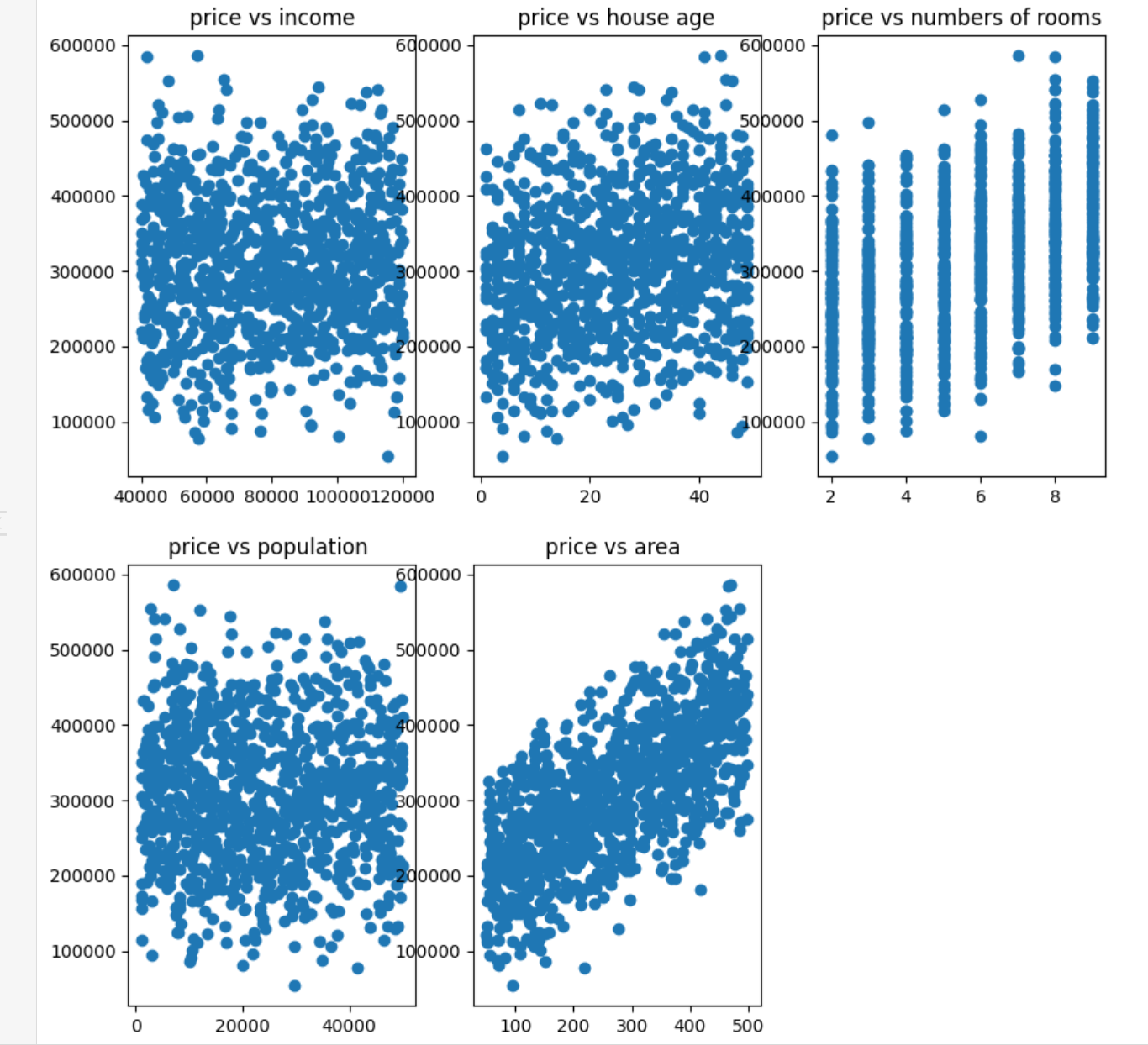
plt.figure(figsize=(10,10))
fig1 = plt.subplot(231) #生成两行三列的子图,且当前为子图1
plt.scatter(data.loc[:,'income'],data.loc[:,'price'])
plt.title('price vs income')
fig2 = plt.subplot(232) #生成两行三列的子图,且当前为子图1
plt.scatter(data.loc[:,'house age'],data.loc[:,'price'])
plt.title('price vs house age')
fig3 = plt.subplot(233) #生成两行三列的子图,且当前为子图1
plt.scatter(data.loc[:,'numbers of rooms'],data.loc[:,'price'])
plt.title('price vs numbers of rooms')
fig4 = plt.subplot(234) #生成两行三列的子图,且当前为子图1
plt.scatter(data.loc[:,'population'],data.loc[:,'price'])
plt.title('price vs population ')
fig5 = plt.subplot(235) #生成两行三列的子图,且当前为子图1
plt.scatter(data.loc[:,'area'],data.loc[:,'price'])
plt.title('price vs area ')
plt.show()
#先来单因素的
x = data.loc[:,'area']
x.head()
y = data.loc[:,'price']
y.head()
建立单因子模型 set up the linear regression model
from sklearn.linear_model import LinearRegression
LR1 = LinearRegression()
train the model
x = np.array(x).reshape(-1,1)
#y = np.array(y).reshape(-1,1)
#print(x.shape)
LR1.fit(x,y)
a = LR1.coef_
b = LR1.intercept_
print(a,b)
y_predict_1 = LR1.predict(x)
print(y_predict_1)
#评估模型
from sklearn.metrics import mean_squared_error,r2_score
mean_squared_error1 = mean_squared_error(y,y_predict_1)
r2_score1 = r2_score(y,y_predict_1)
print(mean_squared_error1,r2_score1)
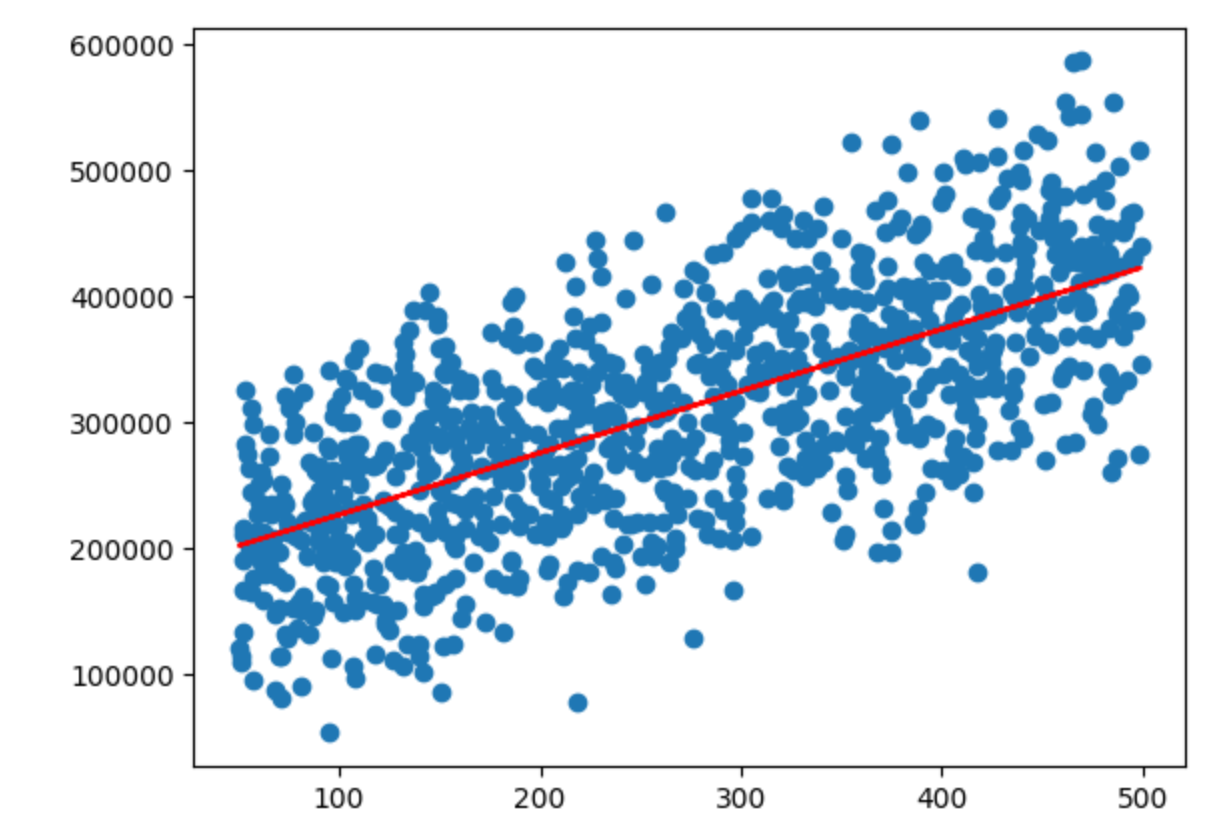
fig6 = plt.figure()
plt.scatter(x,y)
plt.plot(x,y_predict_1,'r')
plt.show()
多因素线性回归
x_multi = data.drop('price',axis=1) #axis=1指定删除的是列,如果是axis=0则为指定删除的是行
#设置多因素线性模型
LR_multi = LinearRegression()
LR_multi.fit(x_multi,y)
#评估模型好坏
y_predict_multi = LR_multi.predict(x_multi)
mean_squared_error_multi = mean_squared_error(y,y_predict_multi)
r2_score_multi = r2_score(y,y_predict_multi)
print(mean_squared_error_multi,r2_score_multi)
#画图看下预测的y和实际的y
fig7 = plt.figure()
plt.scatter(y_predict_multi,y)
#plt.plot(x_multi,y_predict_multi)
plt.show()
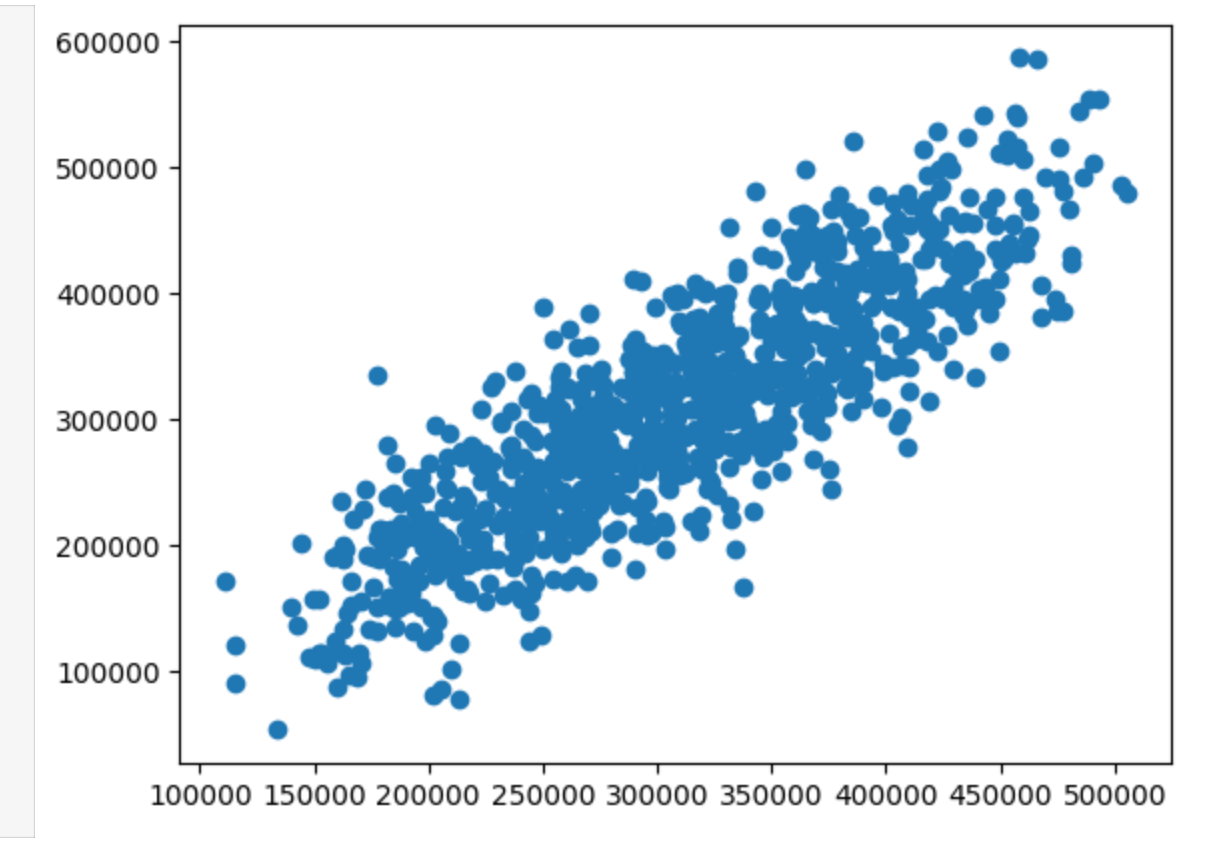
fig8 = plt.figure()
plt.scatter(y_predict_1,y) #单因素的做下对比
plt.show()
相对来说,还是多因素更好些,收敛的更趋近于一条直线。