【递归算法】求根节点到叶节点数字之和

一、题目解析

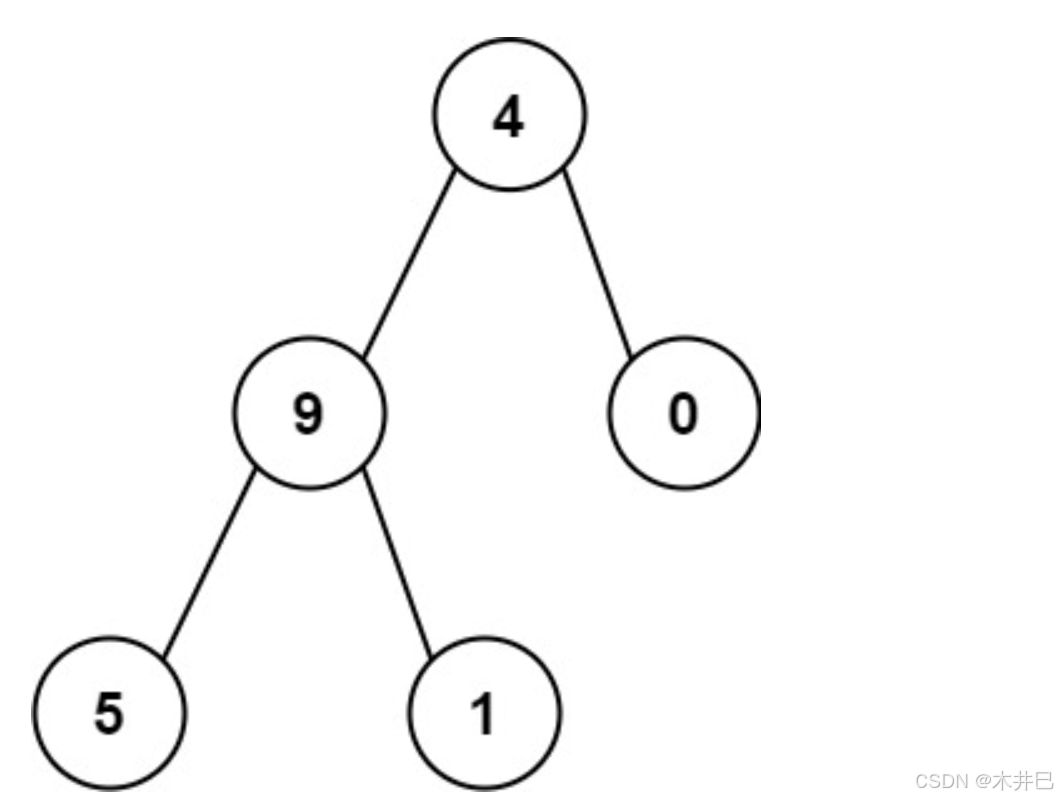
从根节点出发到各个叶结点的路径如下：

4 ------> 9 ------> 5

4 ------> 9 ------> 1

4 ------> 0

每条路径的值组成一个数字，那么三条路径组成的数字分别是：

495，491，40

将这三个数字相加就是最终结果：

495 + 491 + 40 = 1026

二、算法原理

看到二叉树，就说明可以使用递归来解决。

对于每一个节点，我们可以将它们看作：从本身出发到各个叶节点的所有路径组成的数字之和。

比如节点4，从这个节点出发到各个叶节点的路径组成的数字分别是495、491和40，

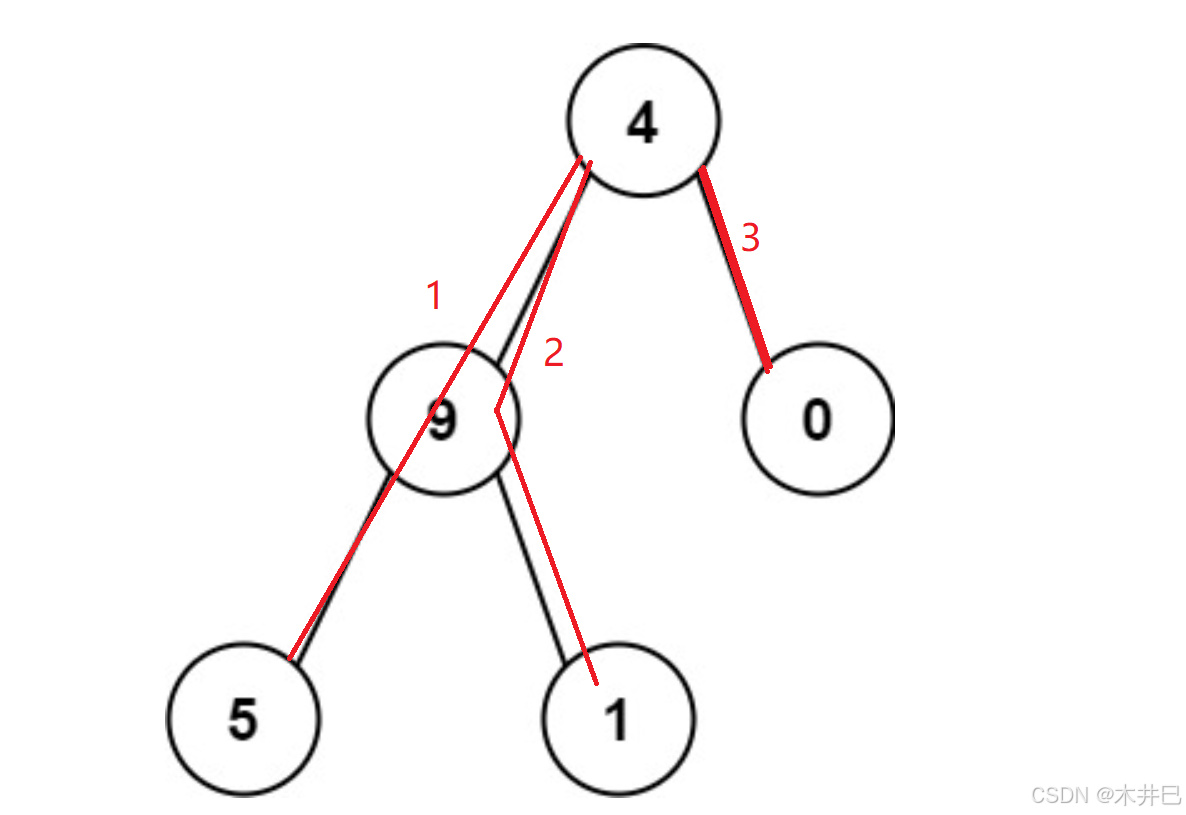
又比如节点9，从这个节点出发到各个叶节点的路径组成的数字分别是95和91：

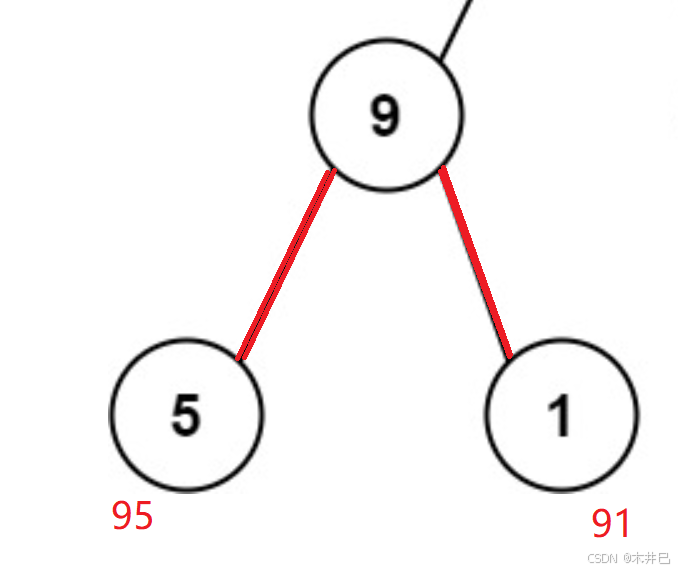
再加上前面的路径数字（4）就是：495和491

对于叶子节点比如5节点、1节点和0节点，它们不存在左右子节点，因此只需要根据前面路径的数字计算出新的路径数字即可。

比如5节点，它根据前面路径数字（49）计算的新的路径数字是：495

1节点根据前面路径数字（49）计算的新路径数字是：491

0节点根据前面路径数字（4）计算的新路径数字是：40

所以这就是重复的子问题，在递归的时候需要知道前面路径组成的数字，因此需要有一个记录路径数字的参数，同时要有一个根节点作为参数（树递归的必要条件），故函数头我们可以设计成：返回值是路径数字类型（即 int），函数的参数有两个，分别是根节点和路径数字：

复制代码

int dfs(TreeNode root, int num);

每一个子问题的具体工作如下：

需要根据前面的路径所组成的数字计算出新的路径数字，

接着将这个新的路径数字作为参数传给左右子节点，这样进行递归，

最后接收左右子树返回的路径数字，相加、返回。

当遇到叶节点时，不再需要递归，只需要计算出新的路径数字，然后返回这个路径数字即可。

需要注意的细节问题：

在判断函数出口之前先计算数字
由于节点的左子节点/右子节点可能为空，需要在递归之前进行判空

三、代码实现

根据算法原理，模拟走一遍的过程：

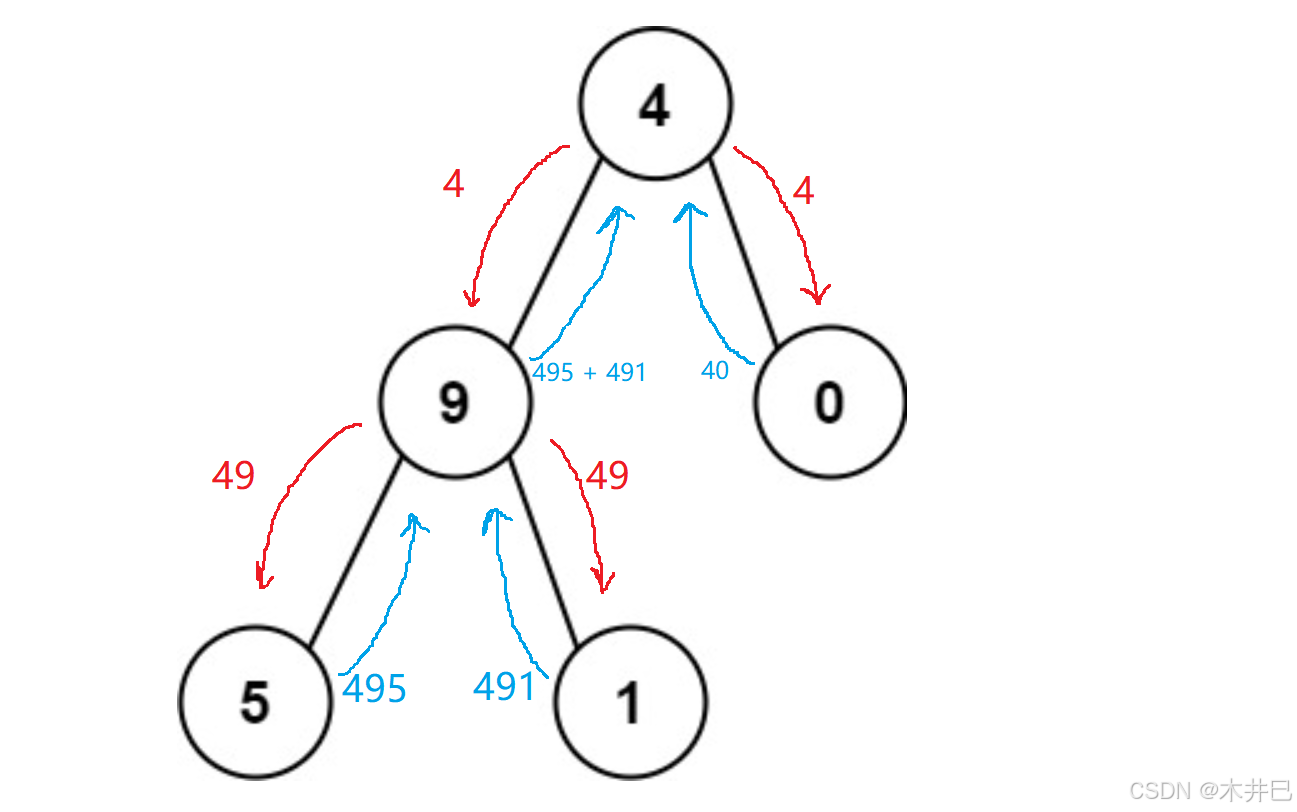
代码如下：

Java 复制代码

class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root, 0);
    }

	public int dfs(TreeNode root, int num) {
		// 根据前面路径的数字计算新的路径数字
		num = num * 10 + root.val;
		// 判断递归出口
		if (root.left == null && root.right == null) return num;
		// 递归（注意判空）
		int ret = 0;
		if (root.left != null) ret += dfs(root.left, num);
		if (root.right != null) ret += dfs(root.right, num);
		// 返回结果
		return ret;
	}
}

完