数据结构基础：图论基础全面解析

引言：为什么我们需要"图"？

在现实世界中，很多事物之间的关系并不是简单的"一对一"或"一对多"能描述的。比如：

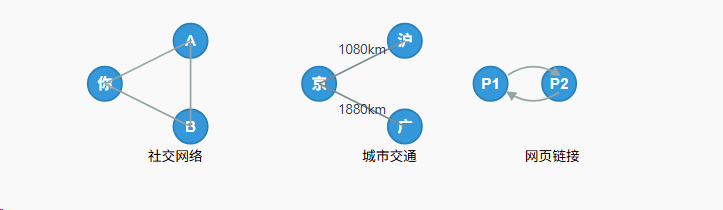
• 社交网络： 你和你的朋友们，每个人是一个点（顶点 ），朋友关系就是一条线（边）。
• **城市交通：**每个城市是一个点，城市之间的公路是一条线。
• **网页链接：**每个网页是一个点，网页A跳转到网页B的链接就是一条有方向的线。

这些"多对多"的关系网络，就是"图"（Graph）数据结构要描述的问题。图是一种用来表示物体与物体之间复杂关系的非线性数据结构。

1、图的基本概念

一个图 G 由两个集合组成：顶点 集 V 和 边 集 E。我们通常记为 G = (V, E)。下面是学习图必备的词汇：

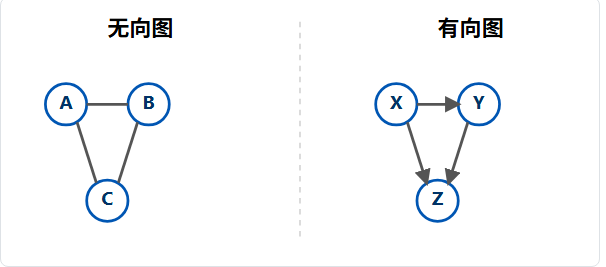
1.1、有向图和无向图

这是对"关系"最基本的分类。

• 无向图：边是没有方向的。如果 A 和 B 之间有边，意味着 A 到 B 和 B 到 A 是等价的。比如"好友关系"、"公路相连"。
• 有向图 ：边是有方向的。A 到 B 的边（表示为 <A, B>）和 B 到 A 的边（<B, A>）是不同的。比如"关注关系"（A 关注 B，不代表 B 关注 A）、"超链接"。

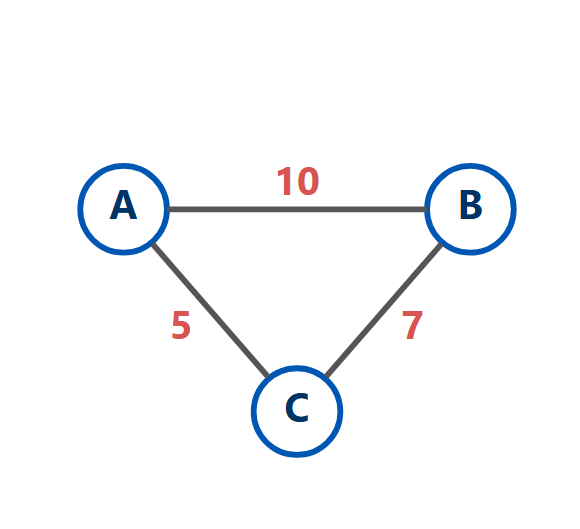
1.2、带权图和无权图

这是对"关系强度"的描述。

• 无权图：所有边都一样，只关心"有"或"没有"连接。
• 带权图：每条边都有一个关联的数值（权重），表示这个连接的"成本"、"距离"或"强度"。比如地图上的公路距离。

1.3、顶点的度

"度"是衡量一个顶点"繁忙"或"重要"程度的最基本指标。

• 无向图的度 ：一个顶点A的度 (deg(A)) 是指直接连接到A的边的数量 。在1.1图示例中，deg(A) = 2, deg(B) = 2, deg(C) = 2。
• 有向图的度 ：在有向图中，关系有方向，因此"度"被细分为：
  • 入度 ：指向该顶点的边的数量。
  • 出度 ：从该顶点出发的边的数量。

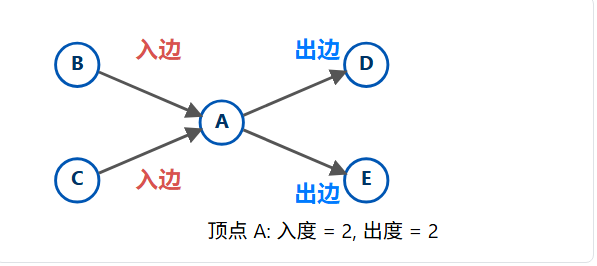
为什么要区分"度"？

"度"是分析节点影响力的最基本指标。

在有向图中，入度和出度的含义截然不同。以社交网络（有向图）为例：

• 高入度：意味着很多人"关注"你（例如微博、Twitter）。这是"影响力"或"受欢迎程度"的体现。
• 高出度：意味着你"关注"了很多人。这可能是"信息获取者"或"活跃用户"的体现。

很多图算法的起点就是基于对"度"的分析。

1.4、路径

路径是从一个顶点到另一个顶点所经过的顶点序列。一条路径由一系列的边连接而成。

• 简单路径 ：一条路径中，所有顶点（除了可能的起点和终点）只出现一次。这是我们最常讨论的路径类型。
• 路径长度：路径上边的数量（无权图）或边的权重之和（带权图）。

一条从 A 到 F 的简单路径: A → C → D → F (长度为3)

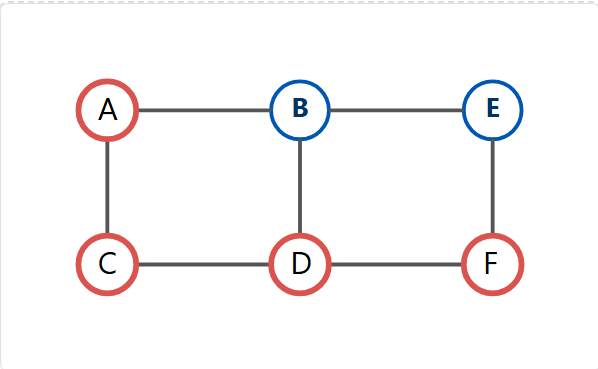
为什么"路径"如此重要？

**路径是"可达性"和"成本"的量化。**图算法的核心问题几乎都与路径相关：

• 可达性问题："A能到F吗？" ------ 这个问题等价于 "A和F之间存在路径吗？" (BFS/DFS 可以解决)
• 最短路径问题："A到F最近的路怎么走？" ------ 这个问题是 "A到F的最短路径长度是多少？" (BFS / Dijkstra 算法可以解决)

1.5、环

环是一条特殊的路径，它的起点和终点是同一个顶点。一个简单的环是指除了起点/终点相同外，其他顶点不重复的环。

• 无向图中的环：很容易理解，像"B-C-D-B"这样的闭合回路。
• 有向图中的环 ：必须严格遵循箭头方向 。例如，A → B → C → A 是一个环；但 A → B ← C ← A 这不是一个环，而只是两组边。

一个有向环: B → C → D → E → B

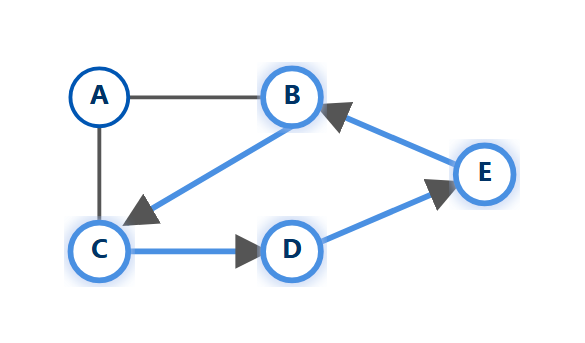
为什么要关心"环"？

**环代表"依赖"或"死循环"。**检测环的存在是图算法的一个重要应用：

• 任务调度 (有向图) ：如果你有一个任务依赖图（A必须先于B，B必须先于C），如果出现一个环 (A → B → C → A)，则意味着这个任务永远无法完成！(A等C，C等B，B等A)。这种没有环的有向图称为"有向无环图"(DAG)，它至关重要。
• 死锁检测：在操作系统中，如果进程A在等待进程B的资源，而B在等待A的资源，这就形成了一个环，导致死锁。

1.6、连通性

连通性描述的是图中顶点之间"相互到达"的程度。这个概念在无向图和有向图中差异很大。

1. 无向图：连通图 vs. 连通分量

• 连通图 ：如果一个无向图中，任意 两个顶点之间都存在路径，则称该图为连通图。
• 连通分量：如果一个无向图不是连通的，它会自然地"碎裂"成几个独立的子图，每个子图内部是连通的。这些独立的子图就叫作"连通分量"。

一个包含 3 个连通分量 ( {A,B,C}, {D,E}, {F} ) 的无向图

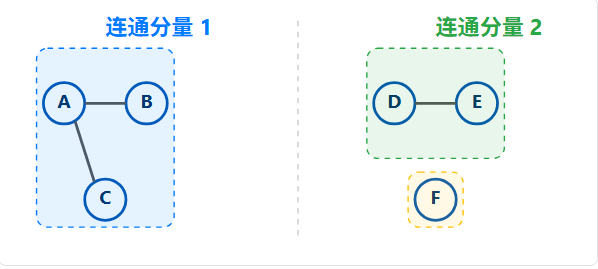
2. 有向图：强连通 vs. 弱连通

• 强连通图 ：这是最严格的连通。如果一个有向图中，任意 两个顶点 u 和 v，都存在一条从 u 到 v 的路径 并且 存在一条从 v 到 u 的路径。这意味着图中的每个点都可以"互相到达"。
• 弱连通图：如果我们"忽略"边的方向（即把所有有向边都当作无向边），得到的无向图是连通的，那么原有向图就是弱连通的。

为什么"连通性"如此重要？

连通性决定了"信息的流动"和"系统的划分"。

• 连通分量：(无向图) 告诉你一个网络被分成了多少个"小岛"。在社交网络中，这可以帮你识别不同的社群或圈子。在网络诊断中，如果你的电脑和打印机不在一个连通分量里，它们就无法通信。
• 强连通：(有向图) 这是一个非常"健壮"的结构。在一个强连通的交通网络中，无论发生什么（比如修路），你总能找到另一条路从A到B（也总能从B开回A）。

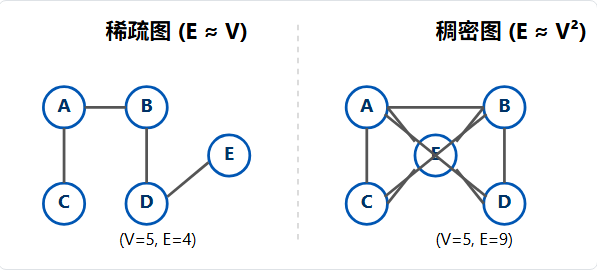
1.7、稠密图 和 稀疏图

这是一个基于"边-点"数量关系的实用分类。假设 V 是顶点数，E 是边数。

一个完全图 （任意两点间都有边）的边数大约是 V² / 2。我们以此为基准：

• 稀疏图 ：边的数量 E 远远小于 V²。通常 E 和 V 差不多是同一个数量级（例如 E 约等于 O(V)）。
• 稠密图 ：边的数量 E 接近 V²。也就是说，大部分顶点对之间都存在边。

为什么这很重要？

选择"稠密"还是"稀疏"的存储方式，会极大地影响算法的空间复杂度 和时间复杂度。我们将在下一章详细探讨。

2、图的数学性质

图作为一种数学模型，具有一些非常优美和实用的性质。理解它们有助于我们更深刻地认识图的结构和算法的边界。

2.1、握手定理

这是一个关于无向图 的基本定理：图中所有顶点的度数之和，等于边数的两倍。

∑ deg(v) = 2 * E

其中 deg(v) 是顶点 v 的度，E 是边数。

为什么是两倍？

这个道理非常直观。想象一下你和朋友们握手：

• 每一条"边"代表一次"握手"。
• 每一次"握手"都恰好连接了"两个"顶点（两个人）。
• 当我们去统计每个顶点的"度"（每个人握了多少次手）并把它们加起来时，A说"我握了手"，B也说"我握了手"。
• 对于连接 A 和 B 的那条边（那次握手），它既被 A 统计了一次，也被 B 统计了一次。

因此，每一条边在"度数之和"中都恰好被计算了两次。所以，总度数和 = 2 * 总边数。

重要推论：在一个无向图中，度数为奇数的顶点，其个数必定是偶数。

为什么奇数度的顶点必为偶数个？

我们知道总度数和 (2 * E) 必定是一个偶数。

这个总和可以被拆分为两部分：所有偶数度顶点的度数之和（这部分肯定是偶数），加上所有奇数度顶点的度数之和。

总和(偶) = 偶数度之和(偶) + 奇数度之和( ? )

为了使等式成立，奇数度顶点的度数之和也必须是偶数。

而"奇数 + 奇数 = 偶数"。要想让一堆奇数相加得到一个偶数，这堆奇数的个数必须是偶数个（例如 3+5=8 (2个)，3+5+7=15 (3个)，3+5+7+9=24 (4个)）。

应用：这个推论是著名的"欧拉路径"问题（例如"一笔画"问题）的理论基础。

2.2、有向图的度定理

在有向图 中，存在一个类似的定理：所有顶点的"入度"之和，等于所有顶点的"出度"之和，等于图的边数 E。

∑ in-deg(v) = ∑ out-deg(v) = E

****为什么？

这也非常直观。每一条有向边 e = (u, v) 都：

• 从一个顶点 u "出发"，为 u 的出度贡献 +1。
• 指向一个顶点 v "进入"，为 v 的入度贡献 +1。

当你把所有顶点的"出度"加起来时，你就是在计算"总共有多少条边出发了"，这等于总边数 E。

当你把所有顶点的"入度"加起来时，你就是在计算"总共有多少条边进入了"，这也等于总边数 E。

2.3、完全图

完全图（K_n）是一个简单的无向图 ，其中 任意 两个不同的顶点之间都恰好有一条边相连。

一个有 n 个顶点的完全图（K_n）有 E = n * (n - 1) / 2 条边。

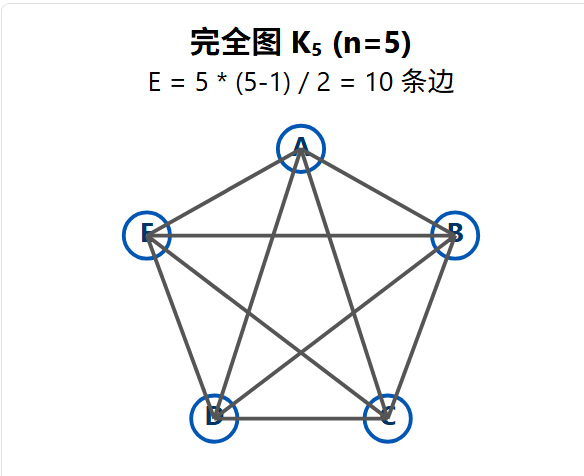
为什么是 n * (n - 1) / 2？

方法一（握手定理） ：在 K_n 中，每个顶点都和其它所有 (n-1) 个顶点相连。所以，每个顶点的度数都是 (n-1)。总共有 n 个顶点，所以总度数和 ∑ deg(v) = n * (n - 1)。根据握手定理，边数 E = 总度数 / 2，即 E = n * (n - 1) / 2。

方法二（组合数学） ：一条边就是从 n 个顶点中"选出2个顶点"的一种组合。从 n 个元素中取 2 个的组合数 (C(n, 2)) 是多少？ C(n, 2) = n! / (2! * (n-2)!) = (n * (n-1)) / 2。

2.4、树的性质

树是一种特殊的图，它是图论中最重要的结构之一。

定义 ：一个连通的 、无环的无向图。

核心性质：一个有 n 个顶点的树，必定恰好有 n-1 条边。

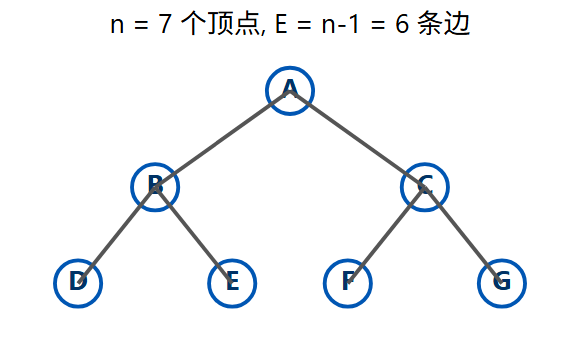
为什么是 n-1 条边？

你可以想象"构造"一棵树的过程：

1. 从 1 个顶点开始 (n=1, E=0)。E = n-1 成立。
2. 加入第 2 个顶点，并用 1 条边将它连接到第 1 个顶点 (n=2, E=1)。E = n-1 成立。
3. 加入第 3 个顶点，并用 1 条边将它连接到已有的任意一个 顶点上 (n=3, E=2)。E = n-1 成立。

你每加入一个新顶点，都必须（且只能）用1 条边将它连到已有的树上。加 2 条边就会产生环，不加边它就不连通。这个过程重复 n-1 次（加入 n-1 个新顶点），所以你总共添加了 n-1 条边。

等价定义：以下任意两个条件都可以定义一个树（对于n>0的图）：

• (1) 连通的
• (2) 无环的
• (3) 有 n-1 条边

任意两个条件组合，都可以推出第三个。例如：一个连通的、有 n-1 条边的图，必定无环。一个无环的、有 n-1 条边的图，必定连通。

2.5、图的同构

"同构"是图论中的"全等"概念。如果两个图 G1 和 G2 结构完全相同，只是顶点（和边）的"名字"不同，或者"画法"不同，我们就称它们是同构的。

形式化定义 ：G1 与 G2 同构，是指存在一个双射（一对一且全覆盖）函数 f: V(G1) → V(G2)，使得 G1 中的任意两个顶点 u 和 v 之间有边，当且仅当 G2 中的 f(u) 和 f(v) 之间也有边。

如何判断？ 这是一个著名的难题（"图同构问题"，目前没有已知的多项式时间解法）。但要证明两个图不同构，则相对容易，我们只需找到一个"结构性"的差异即可，例如：

• 顶点数量或边数量不同。
• 顶点的"度数序列"（所有顶点的度数列表）不同。
• 环的长度或数量不同。

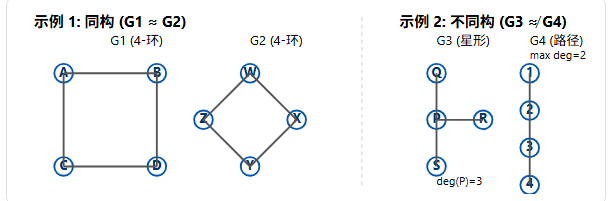
为什么"同构"很重要？

**它关注的是"结构"而非"标签"。**在化学中，两种化合物（图）可能有不同的命名（标签），但如果它们的分子结构（图）是同构的，那么它们就是同一种物质。

在 G3 和 G4 的例子中，G3 有一个度为3的顶点 P，而 G4 所有的顶点度数都是1或2。它们的"度数序列"（G3: {3, 1, 1, 1} vs G4: {1, 2, 2, 1}）不同，因此它们在结构上不可能是相同的，必定不同构。

2.6、平面图和欧拉公式

平面图 ：一个图，如果它可以被画在 一个平面上，且所有的边仅在顶点处相交（即边与边之间没有交叉），则称它为平面图。

欧拉公式 ：对于任意一个连通的平面图，顶点数(V)、边数(E) 和 面数(F) 之间满足一个恒等式：

V - E + F = 2

• F (面, Faces) ：指由边围成的区域，必须包括图外部的"无限大"区域。

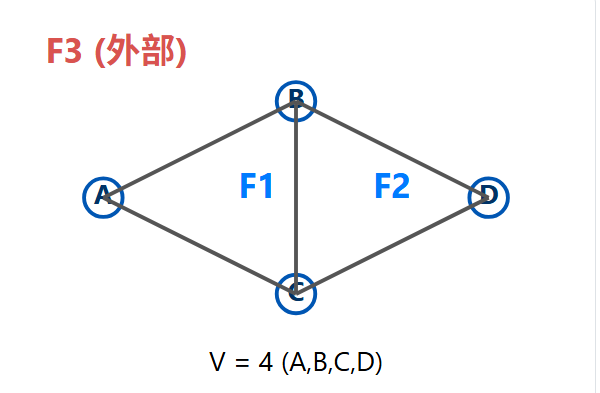
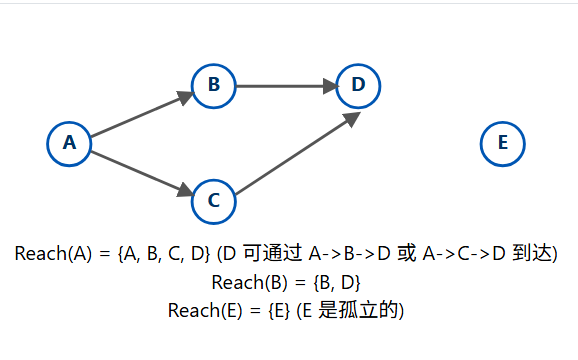
2.7、图的可达性

可达性是图论中最基本的问题之一："从顶点 u 出发，能否到达顶点 v？"

• 定义 ：如果存在一条从 u 到 v 的路径，则称 v 是从 u 可达的。
• 自反性 ：任何顶点 u 总是可达自身的（路径长度为0）。
• 可达集 Reach(u)：从 u 出发，所有可达的顶点的集合。

如何计算可达性？

图的遍历算法 (BFS 和 DFS) 就是为解决可达性问题而生的！

从顶点 u 开始执行一次 BFS 或 DFS：

• 所有被访问到的顶点 ，就是 u 的可达集 Reach(u)。
• 如果你想知道 v 是否从 u 可达，只需启动遍历，看 v 是否在 visited 集合中。

可达性在有向图和无向图中引申出"连通性"的概念：

• 无向图 ：如果 v 从 u 可达，则 u 也必从 v 可达。它们在同一个"连通分量"中。
• 有向图 ：如果 v 从 u 可达，且 u 从 v 可达，则它们在同一个"强连通分量"中。

3、图的存储方式

我们画在纸上的图，计算机如何"理解"并存储呢？这至关重要，因为不同的存储方式决定了算法的效率。

主要有两种方式：邻接矩阵 和 邻接表。

3.1、邻接矩阵

邻接矩阵使用一个 V x V 的二维数组（V 是顶点数）。我们通常需要一个映射（比如数组索引或哈希表）将顶点（如 'A'）映射到矩阵的索引（如 0）。

matrix[i][j] = 1 （或权重）表示从顶点 i 到顶点 j 有一条边。 matrix[i][j] = 0 （或无穷大）表示没有边。

对于无向图 ，这个矩阵是对称 的（matrix[i][j] == matrix[j][i]）因为无向图中 (i,j) 和 (j,i) 表示同一条边，所以 matrix[i][j] == matrix[j][i]，矩阵沿对角线对称。对于有向图，则不一定对称。

为什么使用矩阵？（优缺点）

优点：查询快。 它利用了数组 O(1) 的索引访问特性。想知道"A和B之间有边吗？" 只需要 1 步操作：检查 matrix[0][1] 的值。这非常快。

缺点：空间浪费。 这是它最致命的问题。你需要 V * V 的空间。想象一个有100万用户的社交网络（V=10⁶），你需要一个 10⁶ x 10⁶ 的矩阵，这需要 (10¹²) 个存储单元，是无法承受的！

为什么浪费？ 因为大多数图都是稀疏图。一个用户平均可能只有300个好友，而不是100万个。这意味着矩阵中 99.9% 的元素都是 0。我们为这些 0 浪费了海量空间。

其他缺点：要查找一个顶点的所有邻居，你必须遍历一整行（或一整列），这需要 O(V) 的时间，无论它有 1 个邻居还是 V-1 个邻居。

3.2、邻接表

邻接表是解决空间浪费的完美方案。它是一种"按需分配"的思想。

它使用一个 "数组（或哈希表）+ 链表（或列表）" 的结构。数组的每个索引 i 对应顶点 i，该索引处存储一个列表或链表，列表只包含 i的邻居们。

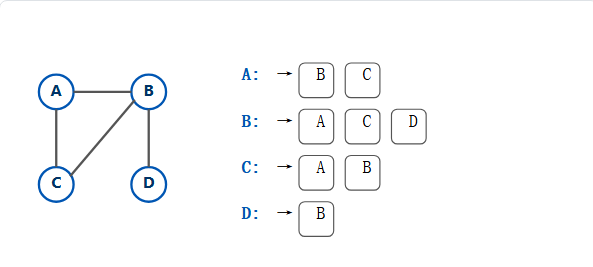
为什么邻接表是首选？（优缺点）

优点：空间高效。 它的空间复杂度是 O(V + E)（V个顶点的数组 + E个边的总数）。对于稀疏图（E 远小于 V²），这比 O(V²) 高效得多。对于100万用户、每人300好友的社交网络：

• V = 10⁶, E ≈ 10⁶ * 300 / 2 (无向图除以2) ≈ 1.5 x 10⁸
• O(V + E) ≈ 10⁶ + 1.5 x 10⁸ ≈ 1.51 x 10⁸

1.5亿 远小于 10¹² (矩阵)，完全可以接受。

其他优点：查找顶点 A 的所有邻居非常快，只需 O(deg(A)) 时间，即 A 的度。这在遍历（BFS, DFS）中效率极高。

**缺点：查询稍慢。**想知道"A和B之间有边吗？" 你不能O(1)完成了。你必须遍历 A 的邻居列表（O(deg(A)) 时间），查看 B 是否在其中。在稠密图中，这可能退化到 O(V)。

3.3、边集数组

这是最简单的存储方式，没有之一。它只关心"有哪些边"。

它使用一个 一维数组 ，数组的每个元素是一个对象（或元组），用于存储一条边。通常存储边的起点、终点和权重（如果有的话）。

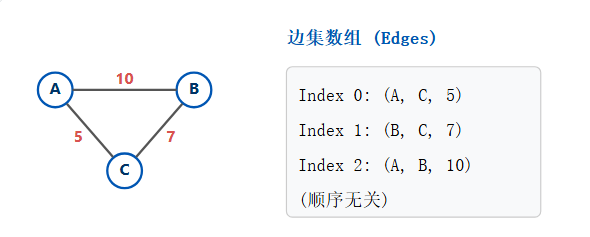
为什么使用边集数组？（优缺点）

**优点：结构简单，空间高效。**空间复杂度为 O(E)。它非常适合那些需要"遍历所有边"的算法。例如，Kruskal 算法（用于找最小生成树）的第一步就是将所有边按权重排序，使用边集数组是完美的选择。

缺点：查询邻居效率极低。 这是它的致命弱点。如果你想"查找A的所有邻居"，你必须遍历整个边集数组（O(E) 时间），检查每一条边的起点或终点是否为 A。在大多数图遍历算法（BFS, DFS）中，这完全无法接受。

3.4、邻接多重表

这种结构主要用于无向图 ，其核心目的是方便对边的操作（例如删除边），并避免邻接表中一条边被存储两次（A的邻居有B，B的邻居有A）。

它由"顶点表"和"边表"组成：

• 顶点表 ：一个数组，每个顶点占一个位置。每个顶点存储：
  • 顶点的数据（如 'A'）。
  • 一个指向第一条依附于它 的边的指针 first_edge。
• 边表 ：一个数组（或链表），每个元素代表一条边 。每个边节点存储：
  • 边的两个顶点 v1, v2。
  • 一个指针 link1，指向依附于 v1 的下一条边。
  • 一个指针 link2，指向依附于 v2 的下一条边。

这就在所有边中，为每个顶点"穿"出了一条独立的链表。

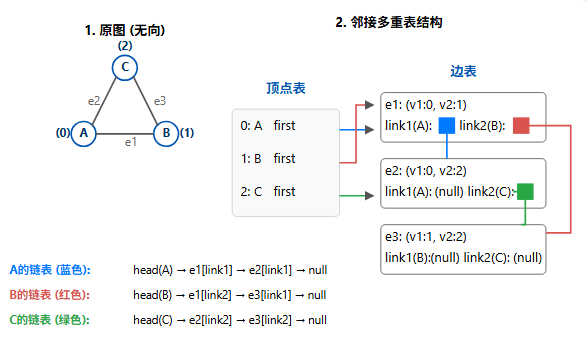
为什么用邻接多重表？（优缺点）

优点：空间效率和边操作。 存储 E 条边只需要 E 个边节点，非常节省空间。最重要的是，删除一条边 （例如 e1）的操作非常高效。你只需要修改 e1 的前驱节点（这里是顶点A和B）和后继节点（e2 和 e3）的指针即可，这比在邻接表中（需要搜索两个链表）要更清晰。

**缺点：实现复杂。**这种精细的指针操作非常容易出错。而且，查找顶点的所有邻居仍然需要 O(deg(V)) 的时间（遍历它所"穿"过的链表）。因此，它只在对边操作有极高要求的特定场景下使用。

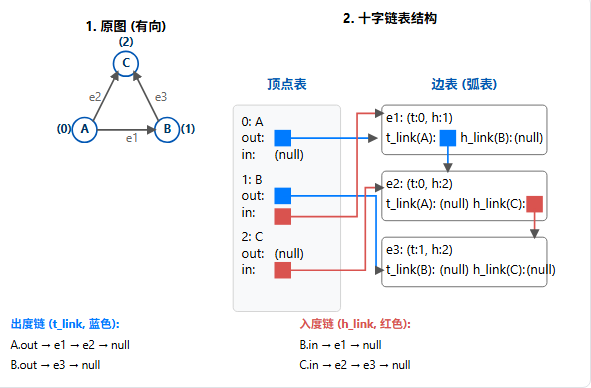
3.5、十字链表

如果说邻接多重表是为无向图优化的，那么十字链表就是为有向图优化的。

它的核心目标是：既能快速找到一个顶点的所有"出边"（出度），也能快速找到所有"入边"（入度）。 邻接表只能高效地做到前者。

它也由"顶点表"和"边表"（或称弧表）组成：

• 顶点表 ：每个顶点存储：
  • 顶点数据（如 'A'）。
  • first_out：指向以它为起点的第一条出边。
  • first_in：指向以它为终点的第一条入边。
• 边表 ：每个边节点存储：
  • 起点（尾）索引 tail。
  • 终点（头）索引 head。
  • t_link（tail link）：指向起点相同的下一条边。
  • h_link（head link）：指向终点相同的下一条边。

这相当于为所有边建立了两个正交的链表集合：一个集合按"起点"链接，另一个集合按"终点"链接。

为什么用十字链表？（优缺点）

**优点：强大的有向图查询能力。**它是唯一一种能让你在 O(out-degree) 时间内找到所有后继（出边），并在 O(in-degree) 时间内找到所有前驱（入边）的结构。邻接表只能高效实现前者。

**缺点：极度复杂且空间开销大。**这是最复杂的图结构之一。每个顶点需要2个指针，每条边需要2个顶点索引+2个指针，空间开销是 O(V+E) 中最大的。

应用：需要频繁计算入度和出度的算法，例如拓扑排序（虽然邻接表也能做，但十字链表更直接），或者需要反向遍历图的场景。

3.6、存储对比

理解了所有存储方式后，我们如何选择？这取决于你的"数据特性"和"操作需求"。

存储方式	空间复杂度	检查边(u,v)	找v的邻居(出)	找v的邻居(入)	实现
邻接矩阵	O(V2)	O(1)	O(V)	O(V) (查列)	简单
邻接表	O(V+E)	O(deg(u))	O(deg(u))	O(V+E) (慢)	中等 (Python简单)
边集数组	O(E)	O(E) (极慢)	O(E) (极慢)	O(E) (极慢)	非常简单
邻接多重表	O(V+E)	O(E) (慢)	O(deg(v))	O(deg(v)) (无向)	复杂
十字链表	O(V+E)	O(deg(u)) (慢)	O(out-deg(v))	O(in-deg(v))	非常复杂

如何选择？------ 决策指南

• 99% 的情况：使用邻接表

为什么？ 现实世界的图几乎都是稀疏图 (E 远小于 V²)。邻接表的空间复杂度 O(V+E) 是最优的，并且它能以 O(deg(v)) 的高效时间找到所有邻居，这正是 BFS 和 DFS 遍历算法所需要的。在 Python 中用字典实现也非常简单。

• 当你的图是稠密图时：使用邻接矩阵

为什么？ 如果 E 已经接近 V²，那么 O(V+E) 和 O(V²) 差别不大了。此时，邻接矩阵 O(1) 的"检查边"速度就成了巨大优势。某些算法（如 Floyd-Warshall 多源最短路径）的动态规划依赖于这种 O(1) 查询，用邻接矩阵实现最合适。

• 当你只关心"所有边"时：使用边集数组

为什么？ 如果你的算法不需要查找特定顶点的邻居，而是要对"所有边"进行操作（例如，按权重排序），那么边集数组是最简单、最高效的。Kruskal 算法是典型例子。

• 当你需要频繁操作有向图的"入度"时：使用十字链表

为什么？ 邻接表找"出边"很快 (adj_list[v])，但找"入边"（谁指向v？）需要遍历整个图 (O(V+E))。如果你的应用需要频繁查询入边（例如，高效实现拓扑排序或反向遍历图），十字链表是唯一高效的结构。

• 当你的无向图需要频繁"删边"时：使用邻接多重表

为什么？ 在邻接表中删除一条边 (u, v) 很麻烦，你得去 u 的列表里删 v，还得去 v 的列表里删 u。在邻接多重表中，边是独立对象，删除它只需 O(1) 的指针操作（前提是已拿到该边对象），逻辑更清晰。

4、图的遍历

"遍历"是指系统地访问图中的每一个顶点。这是所有图算法的基础。最核心的两种遍历方式是：广度优先搜索 (BFS) 和 深度优先搜索 (DFS)。

图遍历就像是你在一个陌生的城市（图）中，有了一张地图（邻接表），你需要一个策略来确保你"不重不漏"地访问每一个路口（顶点）。

遍历是"提问"的基础：

• "从A点出发能到达B点吗？" (可达性)
• "从A点到B点，最少需要经过几个路口？" (最短路径)
• "这个城市有环路吗？" (环检测)
• "这个城市被分成了几个互不相通的区域？" (连通分量)

所有这些问题的答案，都始于一次"聪明的"遍历。

4.1、广度优先搜索

BFS 的策略是"逐层"或"水波纹式"地向外探索。它从一个起始节点开始，访问它所有的直接邻居，然后再访问这些邻居的邻居，以此类推。

核心数据结构：队列 (Queue) (先进先出, FIFO)

算法思想：

1. 将起始节点放入一个队列，并标记为"已访问"。
2. 当队列不为空时：
   1. 从队列头部取出一个节点 u。
   2. 处理 u（例如打印它）。
   3. 遍历 u 的所有邻居 v：
      • 如果 v 从未被访问过：
      • 将其标记为"已访问"。
      • 将其放入队列尾部。

BFS还有一个重要的特性：能找到无权图的最短路径

因为 BFS 是"逐层"推进的。它首先访问所有距离为 1 的节点，然后才访问所有距离为 2 的节点，接着是距离为 3 的节点...

当你从 A 出发，通过 BFS 第一次"发现"B 时，你所走的路径一定是 A 到 B 的最短路径。**为什么？**因为如果存在一条更短的路径（比如少一个节点），BFS 的"逐层"特性决定了它"必定"会先通过那条更短的路径发现 B。这构成了一个反证法。

应用：地图导航中查找"最少换乘"的地铁路线（每条边=1）。

4.2、深度优先搜索

DFS 的策略是"一条路走到黑"。它从一个起始节点开始，选择一个邻居，然后"深入"到该邻居的邻居...直到到达一个"死胡同"（没有未访问的邻居），然后"回溯"到上一个节点，尝试另一条路。

核心数据结构：栈 (Stack) (后进先出, LIFO) 或 递归 (系统调用栈)

算法思想 (递归版 - 更直观)：

1. 创建一个"已访问"集合 visited。
2. 定义一个函数 dfs_visit(u)：
   1. 将 u 标记为"已访问"。
   2. 处理 u（例如打印它）。
   3. 遍历 u 的所有邻居 v：
      • 如果 v 从未被访问过：
      • 递归调用 dfs_visit(v)。
3. 从起始节点 s 开始调用 dfs_visit(s)。

DFS 的"深入"特性，它能帮你维护一条"当前路径"，非常适合环检测和拓扑排序。

环检测 ：当你从 u 访问 v 时，如果 v 已经被访问过了，你需要问一个问题：v 是一个已经"完成探索并回溯"的节点，还是一个"正在探索中"（即 v 是 u 的祖先）的节点？如果是后者，你就找到了一个环！

拓扑排序 ：(针对有向无环图 DAG) DFS 能告诉你"谁先谁后"。当你"完成"一个节点 u 的探索（即它的所有子孙都已被访问）并回溯时，u 一定是在它所有子孙"之后"的。你把这个完成的顺序反转，就是拓扑序。

应用：任务调度（必须先编译A，才能编译B）、课程先修（必须先上C101，才能上C102）。

4.3、两种遍历方式对比

BFS 和 DFS 是图遍历的两种最核心的策略。它们都能访问到所有可达顶点，但访问的顺序和应用的场景截然不同。

特性	BFS (广度优先搜索)	DFS (深度优先搜索)
核心数据结构	队列 (Queue) - FIFO (先进先出)	栈 (Stack) - LIFO (后进先出) (或使用递归)
访问顺序	逐层访问。像水波纹一样，从起点开始，先访问完所有距离为 1 的邻居，再访问所有距离为 2 的邻居...	一条路走到黑。从起点出发，选择一个邻居，然后从该邻居出发继续深入，直到无法再前进，才回溯。
形状	"胖"而"矮"。它会尽可能地横向扩展。	"瘦"而"高"。它会尽可能地纵向深入。
空间复杂度	O(V)。最坏情况（如星形图）下，队列可能需要存储所有 V-1 个邻居。	O(V) (递归栈/显式栈)。最坏情况（如链表图）下，栈的深度可能达到 V。
找到的路径	保证找到最短路径 (在无权图中)。	不保证找到最短路径。找到的路径取决于探索的顺序。
适用场景	+ 无权图最短路径 (如：导航) + 社交网络中"N度好友" + 爬虫（逐层爬取）	+ 寻找路径（任意路径即可） + 拓扑排序 + 寻找连通分量 / 强连通分量 + 检测环

4.4、可视化演示

https://code.juejin.cn/pen/7569070221370064934?embed=true

5、Python实现

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from collections import deque
from typing import List, Dict, Set, Optional, Tuple


class GraphMatrix:
    """使用邻接矩阵存储图"""
    
    def __init__(self, num_vertices: int, directed: bool = False):
        """
        初始化图
        :param num_vertices: 顶点数量
        :param directed: 是否为有向图
        """
        self.num_vertices = num_vertices
        self.directed = directed
        # 初始化邻接矩阵，0表示无边，非0表示权重
        self.matrix = [[0] * num_vertices for _ in range(num_vertices)]
    
    def add_edge(self, src: int, dest: int, weight: int = 1):
        """添加边"""
        if 0 <= src < self.num_vertices and 0 <= dest < self.num_vertices:
            self.matrix[src][dest] = weight
            if not self.directed:
                self.matrix[dest][src] = weight
        else:
            raise ValueError("顶点索引超出范围")
    
    def remove_edge(self, src: int, dest: int):
        """删除边"""
        if 0 <= src < self.num_vertices and 0 <= dest < self.num_vertices:
            self.matrix[src][dest] = 0
            if not self.directed:
                self.matrix[dest][src] = 0
    
    def has_edge(self, src: int, dest: int) -> bool:
        """判断是否存在边"""
        return self.matrix[src][dest] != 0
    
    def get_neighbors(self, vertex: int) -> List[int]:
        """获取某顶点的所有邻居"""
        neighbors = []
        for i in range(self.num_vertices):
            if self.matrix[vertex][i] != 0:
                neighbors.append(i)
        return neighbors
    
    def print_graph(self):
        """打印邻接矩阵"""
        print("\n邻接矩阵表示：")
        print("   ", end="")
        for i in range(self.num_vertices):
            print(f"{i:3}", end="")
        print()
        
        for i in range(self.num_vertices):
            print(f"{i:3}", end="")
            for j in range(self.num_vertices):
                print(f"{self.matrix[i][j]:3}", end="")
            print()


class GraphList:
    """使用邻接表存储图"""
    
    def __init__(self, directed: bool = False):
        """
        初始化图
        :param directed: 是否为有向图
        """
        self.graph = {}  # 字典存储邻接表
        self.directed = directed
    
    def add_vertex(self, vertex):
        """添加顶点"""
        if vertex not in self.graph:
            self.graph[vertex] = []
    
    def add_edge(self, src, dest, weight: int = 1):
        """添加边（可以是加权的）"""
        # 确保顶点存在
        self.add_vertex(src)
        self.add_vertex(dest)
        
        # 添加边（存储为 (目标顶点, 权重) 元组）
        self.graph[src].append((dest, weight))
        if not self.directed:
            self.graph[dest].append((src, weight))
    
    def remove_edge(self, src, dest):
        """删除边"""
        if src in self.graph:
            self.graph[src] = [(v, w) for v, w in self.graph[src] if v != dest]
        if not self.directed and dest in self.graph:
            self.graph[dest] = [(v, w) for v, w in self.graph[dest] if v != src]
    
    def has_edge(self, src, dest) -> bool:
        """判断是否存在边"""
        if src not in self.graph:
            return False
        return any(neighbor == dest for neighbor, _ in self.graph[src])
    
    def get_neighbors(self, vertex) -> List:
        """获取某顶点的所有邻居"""
        return [neighbor for neighbor, _ in self.graph.get(vertex, [])]
    
    def get_neighbors_with_weight(self, vertex) -> List[Tuple]:
        """获取某顶点的所有邻居及权重"""
        return self.graph.get(vertex, [])
    
    def print_graph(self):
        """打印邻接表"""
        print("\n邻接表表示：")
        for vertex in sorted(self.graph.keys()):
            neighbors = self.graph[vertex]
            print(f"{vertex} -> {neighbors}")


class EdgeNode:
    """边节点"""
    def __init__(self, src, dest, weight: int = 1):
        self.src = src      # 起点
        self.dest = dest    # 终点
        self.weight = weight  # 权重
    
    def __repr__(self):
        return f"({self.src}->{self.dest}, w={self.weight})"


class GraphEdgeSet:
    """使用边集表存储图"""
    
    def __init__(self, directed: bool = False):
        """
        初始化图
        :param directed: 是否为有向图
        """
        self.edges = []  # 边的列表
        self.vertices = set()  # 顶点集合
        self.directed = directed
    
    def add_vertex(self, vertex):
        """添加顶点"""
        self.vertices.add(vertex)
    
    def add_edge(self, src, dest, weight: int = 1):
        """添加边"""
        self.vertices.add(src)
        self.vertices.add(dest)
        edge = EdgeNode(src, dest, weight)
        self.edges.append(edge)
        if not self.directed:
            # 无向图需要添加反向边
            reverse_edge = EdgeNode(dest, src, weight)
            self.edges.append(reverse_edge)
    
    def remove_edge(self, src, dest):
        """删除边"""
        self.edges = [e for e in self.edges if not (e.src == src and e.dest == dest)]
        if not self.directed:
            self.edges = [e for e in self.edges if not (e.src == dest and e.dest == src)]
    
    def has_edge(self, src, dest) -> bool:
        """判断是否存在边"""
        return any(e.src == src and e.dest == dest for e in self.edges)
    
    def get_neighbors(self, vertex) -> List:
        """获取某顶点的所有邻居"""
        return [e.dest for e in self.edges if e.src == vertex]
    
    def print_graph(self):
        """打印边集表"""
        print("\n边集表表示：")
        print(f"顶点集: {sorted(self.vertices)}")
        print("边集:")
        for edge in self.edges:
            print(f"  {edge}")


class EdgeBoxNode:
    """邻接多重表的边盒子节点"""
    def __init__(self, i_vertex, j_vertex, weight: int = 1):
        self.mark = False  # 访问标记
        self.i_vertex = i_vertex  # 边的一个顶点
        self.j_vertex = j_vertex  # 边的另一个顶点
        self.weight = weight  # 权重
        self.i_link = None  # 指向下一条依附于i_vertex的边
        self.j_link = None  # 指向下一条依附于j_vertex的边
    
    def __repr__(self):
        return f"Edge({self.i_vertex}<->{self.j_vertex}, w={self.weight})"


class VertexBoxNode:
    """邻接多重表的顶点盒子节点"""
    def __init__(self, data):
        self.data = data  # 顶点数据
        self.first_edge = None  # 指向第一条依附于该顶点的边


class GraphAdjacencyMultiList:
    """邻接多重表（专用于无向图）"""
    
    def __init__(self):
        """初始化图"""
        self.vertices = {}  # 顶点字典 {vertex_data: VertexBoxNode}
    
    def add_vertex(self, vertex):
        """添加顶点"""
        if vertex not in self.vertices:
            self.vertices[vertex] = VertexBoxNode(vertex)
    
    def add_edge(self, src, dest, weight: int = 1):
        """添加边"""
        # 确保顶点存在
        self.add_vertex(src)
        self.add_vertex(dest)
        
        # 创建边节点
        edge = EdgeBoxNode(src, dest, weight)
        
        # 将边插入到src的边链表头部
        edge.i_link = self.vertices[src].first_edge
        self.vertices[src].first_edge = edge
        
        # 将边插入到dest的边链表头部
        edge.j_link = self.vertices[dest].first_edge
        self.vertices[dest].first_edge = edge
    
    def get_neighbors(self, vertex) -> List:
        """获取某顶点的所有邻居"""
        if vertex not in self.vertices:
            return []
        
        neighbors = []
        edge = self.vertices[vertex].first_edge
        
        while edge is not None:
            # 判断当前边的另一端是哪个顶点
            if edge.i_vertex == vertex:
                neighbors.append(edge.j_vertex)
                edge = edge.i_link
            else:
                neighbors.append(edge.i_vertex)
                edge = edge.j_link
        
        return neighbors
    
    def print_graph(self):
        """打印邻接多重表"""
        print("\n邻接多重表表示（无向图）：")
        for vertex_data in sorted(self.vertices.keys()):
            vertex_node = self.vertices[vertex_data]
            edges = []
            edge = vertex_node.first_edge
            
            while edge is not None:
                if edge.i_vertex == vertex_data:
                    edges.append(f"{edge.j_vertex}(w={edge.weight})")
                    edge = edge.i_link
                else:
                    edges.append(f"{edge.i_vertex}(w={edge.weight})")
                    edge = edge.j_link
            
            print(f"{vertex_data} -> {edges}")


class ArcBoxNode:
    """十字链表的弧盒子节点"""
    def __init__(self, tail_vertex, head_vertex, weight: int = 1):
        self.tail_vertex = tail_vertex  # 弧尾（起点）
        self.head_vertex = head_vertex  # 弧头（终点）
        self.weight = weight  # 权重
        self.head_link = None  # 指向弧头相同的下一条弧
        self.tail_link = None  # 指向弧尾相同的下一条弧
    
    def __repr__(self):
        return f"Arc({self.tail_vertex}->{self.head_vertex}, w={self.weight})"


class VertexCrossNode:
    """十字链表的顶点节点"""
    def __init__(self, data):
        self.data = data  # 顶点数据
        self.first_in = None   # 指向第一条入弧
        self.first_out = None  # 指向第一条出弧


class GraphOrthogonalList:
    """十字链表（专用于有向图）"""
    
    def __init__(self):
        """初始化图"""
        self.vertices = {}  # 顶点字典 {vertex_data: VertexCrossNode}
    
    def add_vertex(self, vertex):
        """添加顶点"""
        if vertex not in self.vertices:
            self.vertices[vertex] = VertexCrossNode(vertex)
    
    def add_edge(self, src, dest, weight: int = 1):
        """添加边"""
        # 确保顶点存在
        self.add_vertex(src)
        self.add_vertex(dest)
        
        # 创建弧节点
        arc = ArcBoxNode(src, dest, weight)
        
        # 将弧插入到src的出弧链表头部
        arc.tail_link = self.vertices[src].first_out
        self.vertices[src].first_out = arc
        
        # 将弧插入到dest的入弧链表头部
        arc.head_link = self.vertices[dest].first_in
        self.vertices[dest].first_in = arc
    
    def get_out_neighbors(self, vertex) -> List:
        """获取某顶点的所有出邻居（后继）"""
        if vertex not in self.vertices:
            return []
        
        neighbors = []
        arc = self.vertices[vertex].first_out
        
        while arc is not None:
            neighbors.append(arc.head_vertex)
            arc = arc.tail_link
        
        return neighbors
    
    def get_in_neighbors(self, vertex) -> List:
        """获取某顶点的所有入邻居（前驱）"""
        if vertex not in self.vertices:
            return []
        
        neighbors = []
        arc = self.vertices[vertex].first_in
        
        while arc is not None:
            neighbors.append(arc.tail_vertex)
            arc = arc.head_link
        
        return neighbors
    
    def print_graph(self):
        """打印十字链表"""
        print("\n十字链表表示（有向图）：")
        for vertex_data in sorted(self.vertices.keys()):
            vertex_node = self.vertices[vertex_data]
            
            # 打印出弧
            out_arcs = []
            arc = vertex_node.first_out
            while arc is not None:
                out_arcs.append(f"{arc.head_vertex}(w={arc.weight})")
                arc = arc.tail_link
            
            # 打印入弧
            in_arcs = []
            arc = vertex_node.first_in
            while arc is not None:
                in_arcs.append(f"{arc.tail_vertex}(w={arc.weight})")
                arc = arc.head_link
            
            print(f"{vertex_data}:")
            print(f"  出弧: {out_arcs}")
            print(f"  入弧: {in_arcs}")


class GraphTraversal:
    """图的遍历算法（基于邻接表）"""
    
    @staticmethod
    def dfs_recursive(graph: GraphList, start, visited: Set = None) -> List:
        """
        深度优先搜索 - 递归实现
        :param graph: 图对象（邻接表）
        :param start: 起始顶点
        :param visited: 已访问顶点集合
        :return: 遍历顺序列表
        """
        if visited is None:
            visited = set()
        
        result = []
        
        def dfs(vertex):
            visited.add(vertex)
            result.append(vertex)
            print(f"访问节点: {vertex}")
            
            # 递归访问所有未访问的邻居
            for neighbor, _ in graph.graph.get(vertex, []):
                if neighbor not in visited:
                    dfs(neighbor)
        
        dfs(start)
        return result
    
    @staticmethod
    def dfs_iterative(graph: GraphList, start) -> List:
        """
        深度优先搜索 - 迭代实现（使用栈）
        :param graph: 图对象（邻接表）
        :param start: 起始顶点
        :return: 遍历顺序列表
        """
        visited = set()
        stack = [start]
        result = []
        
        while stack:
            vertex = stack.pop()
            
            if vertex not in visited:
                visited.add(vertex)
                result.append(vertex)
                print(f"访问节点: {vertex}")
                
                # 将所有未访问的邻居压入栈
                neighbors = [n for n, _ in graph.graph.get(vertex, [])]
                for neighbor in reversed(neighbors):  # 反转以保持顺序
                    if neighbor not in visited:
                        stack.append(neighbor)
        
        return result
    
    @staticmethod
    def bfs(graph: GraphList, start) -> List:
        """
        广度优先搜索（使用队列）
        :param graph: 图对象（邻接表）
        :param start: 起始顶点
        :return: 遍历顺序列表
        """
        visited = set()
        queue = deque([start])
        visited.add(start)
        result = []
        
        while queue:
            vertex = queue.popleft()
            result.append(vertex)
            print(f"访问节点: {vertex}")
            
            # 将所有未访问的邻居加入队列
            for neighbor, _ in graph.graph.get(vertex, []):
                if neighbor not in visited:
                    visited.add(neighbor)
                    queue.append(neighbor)
        
        return result
    
    @staticmethod
    def dfs_all_paths(graph: GraphList, start, end) -> List[List]:
        """
        找出从start到end的所有路径（DFS应用）
        :param graph: 图对象
        :param start: 起始顶点
        :param end: 目标顶点
        :return: 所有路径的列表
        """
        all_paths = []
        
        def dfs(current, target, path, visited):
            if current == target:
                all_paths.append(path.copy())
                return
            
            visited.add(current)
            
            for neighbor, _ in graph.graph.get(current, []):
                if neighbor not in visited:
                    path.append(neighbor)
                    dfs(neighbor, target, path, visited)
                    path.pop()
            
            visited.remove(current)
        
        dfs(start, end, [start], set())
        return all_paths
    
    @staticmethod
    def bfs_shortest_path(graph: GraphList, start, end) -> Optional[List]:
        """
        使用BFS找最短路径（无权图）
        :param graph: 图对象
        :param start: 起始顶点
        :param end: 目标顶点
        :return: 最短路径，如果不存在则返回None
        """
        if start == end:
            return [start]
        
        visited = {start}
        queue = deque([(start, [start])])
        
        while queue:
            vertex, path = queue.popleft()
            
            for neighbor, _ in graph.graph.get(vertex, []):
                if neighbor not in visited:
                    new_path = path + [neighbor]
                    
                    if neighbor == end:
                        return new_path
                    
                    visited.add(neighbor)
                    queue.append((neighbor, new_path))
        
        return None


def test_graph_implementations():
    """测试所有图的实现"""
    
    print("=" * 60)
    print("测试1: 邻接矩阵 - 无向图")
    print("=" * 60)
    g1 = GraphMatrix(4, directed=False)
    g1.add_edge(0, 1, 1)
    g1.add_edge(0, 2, 1)
    g1.add_edge(1, 3, 1)
    g1.add_edge(2, 3, 1)
    g1.print_graph()
    print(f"顶点0的邻居: {g1.get_neighbors(0)}")
    print(f"是否存在边(0,1): {g1.has_edge(0, 1)}")
    
    print("\n" + "=" * 60)
    print("测试2: 邻接表 - 无向图")
    print("=" * 60)
    g2 = GraphList(directed=False)
    g2.add_edge('A', 'B', 5)
    g2.add_edge('A', 'C', 3)
    g2.add_edge('B', 'D', 2)
    g2.add_edge('C', 'D', 4)
    g2.print_graph()
    print(f"顶点A的邻居: {g2.get_neighbors('A')}")
    print(f"顶点A的邻居（含权重）: {g2.get_neighbors_with_weight('A')}")
    
    print("\n" + "=" * 60)
    print("测试3: 边集表 - 无向图")
    print("=" * 60)
    g3 = GraphEdgeSet(directed=False)
    g3.add_edge('X', 'Y', 10)
    g3.add_edge('Y', 'Z', 20)
    g3.add_edge('X', 'Z', 15)
    g3.print_graph()
    
    print("\n" + "=" * 60)
    print("测试4: 邻接多重表 - 无向图")
    print("=" * 60)
    g4 = GraphAdjacencyMultiList()
    g4.add_edge('A', 'B', 1)
    g4.add_edge('A', 'C', 2)
    g4.add_edge('B', 'C', 3)
    g4.add_edge('B', 'D', 4)
    g4.print_graph()
    
    print("\n" + "=" * 60)
    print("测试5: 十字链表 - 有向图")
    print("=" * 60)
    g5 = GraphOrthogonalList()
    g5.add_edge('A', 'B', 1)
    g5.add_edge('A', 'C', 2)
    g5.add_edge('B', 'C', 3)
    g5.add_edge('C', 'D', 4)
    g5.add_edge('D', 'A', 5)
    g5.print_graph()
    
    print("\n" + "=" * 60)
    print("测试6: DFS遍历 - 递归")
    print("=" * 60)
    g_traverse = GraphList(directed=False)
    g_traverse.add_edge('A', 'B')
    g_traverse.add_edge('A', 'C')
    g_traverse.add_edge('B', 'D')
    g_traverse.add_edge('B', 'E')
    g_traverse.add_edge('C', 'F')
    g_traverse.add_edge('E', 'F')
    result = GraphTraversal.dfs_recursive(g_traverse, 'A')
    print(f"DFS遍历结果: {result}")
    
    print("\n" + "=" * 60)
    print("测试7: DFS遍历 - 迭代")
    print("=" * 60)
    result = GraphTraversal.dfs_iterative(g_traverse, 'A')
    print(f"DFS遍历结果: {result}")
    
    print("\n" + "=" * 60)
    print("测试8: BFS遍历")
    print("=" * 60)
    result = GraphTraversal.bfs(g_traverse, 'A')
    print(f"BFS遍历结果: {result}")
    
    print("\n" + "=" * 60)
    print("测试9: 查找所有路径（DFS应用）")
    print("=" * 60)
    paths = GraphTraversal.dfs_all_paths(g_traverse, 'A', 'F')
    print(f"从A到F的所有路径:")
    for i, path in enumerate(paths, 1):
        print(f"  路径{i}: {' -> '.join(path)}")
    
    print("\n" + "=" * 60)
    print("测试10: 查找最短路径（BFS应用）")
    print("=" * 60)
    shortest = GraphTraversal.bfs_shortest_path(g_traverse, 'A', 'F')
    if shortest:
        print(f"从A到F的最短路径: {' -> '.join(shortest)}")
    else:
        print("未找到路径")


if __name__ == "__main__":
    test_graph_implementations()

# ============================================================
# 测试6: DFS遍历 - 递归
# ============================================================
# 访问节点: A
# 访问节点: B
# 访问节点: D
# 访问节点: E
# 访问节点: F
# 访问节点: C
# DFS遍历结果: ['A', 'B', 'D', 'E', 'F', 'C']

# ============================================================
# 测试7: DFS遍历 - 迭代
# ============================================================
# 访问节点: A
# 访问节点: B
# 访问节点: D
# 访问节点: E
# 访问节点: F
# 访问节点: C
# DFS遍历结果: ['A', 'B', 'D', 'E', 'F', 'C']

# ============================================================
# 测试8: BFS遍历
# ============================================================
# 访问节点: A
# 访问节点: B
# 访问节点: C
# 访问节点: D
# 访问节点: E
# 访问节点: F
# BFS遍历结果: ['A', 'B', 'C', 'D', 'E', 'F']

# ============================================================
# 测试9: 查找所有路径（DFS应用）
# ============================================================
# 从A到F的所有路径:
#   路径1: A -> B -> E -> F
#   路径2: A -> C -> F

# ============================================================
# 测试10: 查找最短路径（BFS应用）
# ============================================================
# 从A到F的最短路径: A -> C -> F

6、总结

1. 图是什么？ - G = (V, E)，一种表示"关系"的通用抽象模型。
2. 如何描述图？ - 有向/无向，带权/无权。
3. 如何存储图？ - 邻接矩阵 (查询快, O(1)，空间 O(V²)，适合稠密图) 和 邻接表 (空间省, O(V+E)，查询稍慢 O(deg)，适合稀疏图，是首选！)。
4. 如何遍历图？
   • BFS (广度优先) ：使用队列 ，逐层探索，能找到无权图最短路径。
   • DFS (深度优先) ：使用栈或递归 ，一条路走到底，适合检测环、拓扑排序。