算法效率
算法效率的优化核心是先定理论复杂度,算法效率的核心是用最少的时间和内存完成相同的功能
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列
long long Fib(int N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 ,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度,时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间,在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎,但是经过计算机行业的迅速发展,计 算机的存储容量已经达到了很高的程度,所以我们如今已经不需要再特别关注一个算法的空间复杂度,更加关注的是时间时间度,同样在校招和春招和实际开发工作中都是十分重要
时间复杂度
时间复杂度的概念
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间,一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道,但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度
找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法
大O渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
O(N^2)
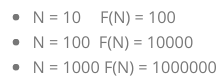
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数, 另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界) 例如:在一个长度为N数组中搜索一个数据x 最好情况:1次找到 最坏情况:N次找到 平均情况:N/2次找到 在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
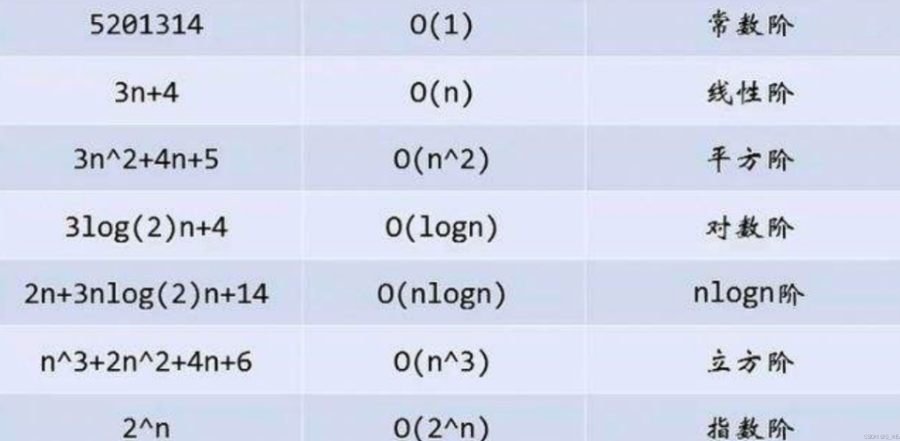
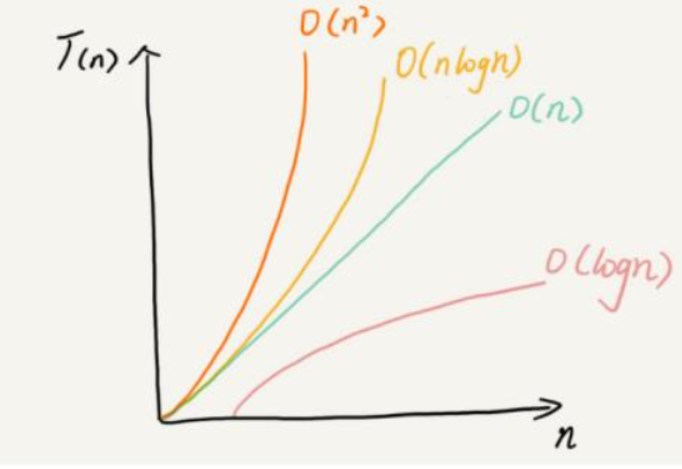
常见的时间复杂度计算
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
步骤 1:统计总基本操作次数
代码里的核心操作是++count,我们统计它的执行次数:
- for 循环 :k<2*N,循环执行2N 次,对应2N次++count;
- while 循环 :M=10,固定执行10 次,对应10次++count;
总操作次数 =2N+10
步骤2:按大O规则化简
大O表示法的两个关键化简原则:
忽略常数系数(比如2N的2);
忽略与 N 无关的固定常数项(比如+10);
因此2N+10化简后为N,时间复杂度即O(N)(常数)
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}步骤 1:统计核心基本操作次数
代码中唯一的重复基本操作是++count,我们统计其总执行次数:
第一个for循环:k<M,循环执行M 次,对应M次++count;
第二个for循环:k<N,循环执行N 次,对应N次++count;
总操作次数=M+N
步骤 2:按大O表示法规则确定复杂度
大O表示法的核心是保留与输入数据量相关的项,忽略常数 / 与数据量无关的固定项,这里的关键是:
M和N是两个相互独立的输入参数 ,因此两者的项都需要保留,不能随意舍弃其中一个,因此总次数M+N直接对应时间复杂度O(M + N)
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}步骤 1:统计核心基本操作次数
代码中唯一的重复操作是++count,for循环条件为k<100,循环固定执行 100 次,对应100次++count;
总操作次数=100
步骤2:按大O表示法规则确定复杂度
大O表示法的核心是描述操作次数随输入数据量增长的趋势 ,如果操作次数不随输入数据量(此处为 N )的变化而变化 ,无论这个固定次数是10、100还是10000,都属于常数级 ,化简后时间复杂度为O(1)
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}最坏情况:数组完全逆序(如5,4,3,2,1)
此时每一趟内层循环都有交换,exchange始终为1,无法提前终止外层循环,外层循环会执行满所有趟数:
外层循环:end从n递减到1,共执行n−1趟(大O表示法忽略常数,记为n趟);
内层循环:第1趟执行n−1次比较,第2趟执行n−2次,......最后1趟执行1次;
总基本操作(比较/交换)次数:(n−1)+(n−2)+...+2+1=n(n−1)/2。
按大O表示法规则化简:n(n−1)/2=1/2*n^2−1/2n,忽略常数系数 和低阶项,最终时间复杂度为O(n2)
最好情况:数组本身已经有序(如1,2,3,4,5)
此时触发exchange的提前终止优化,外层循环仅执行 1 趟就退出:
外层循环:end=n,仅执行1趟;
内层循环:执行n−1次比较,无任何交换,exchange保持0,直接break外层循环;
总基本操作次数:n−1(仅线性次比较)。
按大O规则化简后,时间复杂度为O(n)(这是带优化冒泡排序的核心优势,原始无优化版冒泡排序最好情况也是O(n2))
平均情况:数组随机无序
对于排序算法,平均情况的操作次数与最坏情况同阶,大部分随机无序的数组,都需要执行接近n(n−1)/2次基本操作,因此平均时间复杂度仍为O(n^2)
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号
while (begin <= end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid-1;
else
return mid;
}
return -1;
}步骤拆解:计算循环执行次数
初始查找范围:数组长度为n,区间[0,n-1]包含n个元素;
第1次循环后:排除一半元素,查找范围变为n/2个;
第2次循环后:查找范围继续减半,变为n/4(即n/2^2)个;
...
第k次循环后:查找范围缩小为n/2^k个;
当查找范围缩小到1 个元素时(n/2^k =1),是最后一次有效查找:
对等式变形得:2ᵏ=n→ 两边取2的对数,k=log₂n。
若这最后1个元素仍不是目标值,循环会再执行1次(begin>end)后退出,但常数次的循环不影响时间复杂度的阶数,因此核心循环次数为log₂n
最坏情况
目标值不存在于数组中 ,或目标值是数组的第一个 / 最后一个有效元素,需要执行log₂n次循环。
此时时间复杂度为:O(log₂n)
算法分析中,对数的底数可以省略,因此通常简写为:O(logn)(这是二分查找的标准时间复杂度)
最好情况
第一次计算mid就命中目标值(a[mid]==x),循环仅执行1次就返回结果,时间复杂度为:O(1)
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}计算N!(N的阶乘),基线条件N=0时返回1(0!的数学定义为1),递归关系为N!=(N-1)!×N
1.统计递归调用的总次数
调用Fac(N)会触发一系列链式递归,直到触发基线条件Fac(0),完整的调用链是:
Fac(N)→Fac(N-1)→Fac(N-2)→...→Fac(1)→Fac(0)
总调用次数为N+1 次(包含Fac(0)这次基线条件的调用)。
2.分析单次递归调用的操作时间
每次递归调用内部,仅执行3类常数级操作(与N无关,执行时间固定):
条件判断:if(0==N)
乘法运算:Fac(N-1)*N(仅递归返回后执行的常数级计算)
返回值:return1或return乘积
因此,单次递归调用的时间复杂度为 O(1)
3.计算总时间复杂度
总时间复杂度=调用次数×单次操作时间=(N+1)×O(1)
忽略常数项1和系数,最终总时间复杂度为O(N)
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}递归时间复杂度公式:总时间复杂度 = 递归调用的总次数 × 单次递归调用的操作时间复杂度
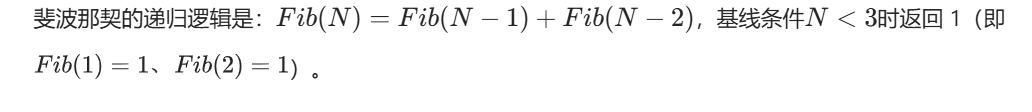
调用Fin(N)会产生二叉分支式 的调用树,而非阶乘的线性链式 调用,比如调用Fib(5)的调用树如下
Fib(5)
/ \
Fib(4) Fib(3)
/ \ / \
Fib(3) Fib(2) Fib(2) Fib(1)
/ \
Fib(2) Fib(1)- 调用数逐层翻倍:第 1 层 1 个、第 2 层 2 个、第 3 层 4 个、第 4 层 8 个...... 符合2k的规律;
- 大量重复调用 :比如
Fib(3)被计算 2 次、Fib(2)被计算 3 次、Fib(1)被计算 2 次,N 越大,重复的次数会呈指数级增长

总调用次数是一个等比数列求和:
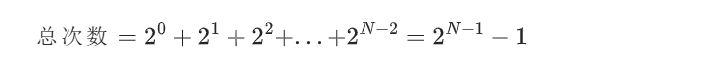
这是效率极低的时间复杂度,因为:
- 指数级增长的特点是「N 稍大,总操作数就会爆炸式增长」:比如Fib(40)总调用次数约百万次,Fib(50)约上亿次,Fib(60)直接达到千亿次;
- 核心原因是大量重复计算 :约 99% 的递归调用都是在重复计算已经算过的斐波那契值,这是这个经典递归版的致命缺陷