《Transformer注意力机制:MHA、MQA、GQA、MLA原理解析与对比》
- 《Transformer注意力机制:MHA、MQA、GQA、MLA原理解析与对比》
- 深入解析:Transformer中的注意力机制演进---MHA、MQA、GQA与MLA深度分析
-
- [1. 多头注意力机制(MHA)](#1. 多头注意力机制(MHA))
-
- 原理与公式推导
-
- 1) 线性投影生成 Q, K, V 线性投影生成 Q, K, V)
- 2) 缩放点积注意力 缩放点积注意力)
- 3) 多头拼接与输出映射 多头拼接与输出映射)
- 局限性
- [2. 多查询注意力(MQA)](#2. 多查询注意力(MQA))
-
- 原理与公式推导
-
- 1) 查询保持独立 查询保持独立)
- 2) 共享Key和Value 共享Key和Value)
- 3) 注意力计算 注意力计算)
- 局限性
- [3. 分组查询注意力(GQA)](#3. 分组查询注意力(GQA))
- [4. 多头潜在注意力(MLA)](#4. 多头潜在注意力(MLA))
- [5. 对比表](#5. 对比表)
- [6. 总结](#6. 总结)
深入解析:Transformer中的注意力机制演进---MHA、MQA、GQA与MLA深度分析
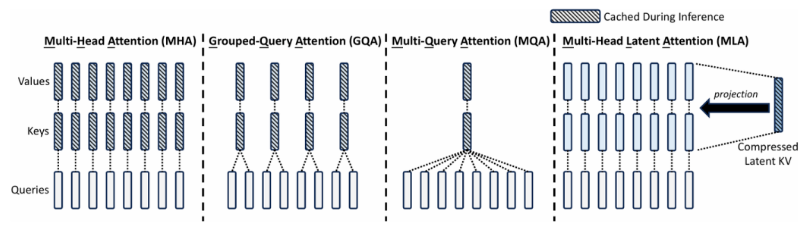
在自然语言处理(NLP)、计算机视觉(CV)等领域的突破性进展中,Transformer架构作为核心模型之一,已经成为众多任务的标准框架。然而,随着模型规模的持续增长,传统的多头注意力机制(MHA)在计算效率和内存消耗方面逐渐暴露出瓶颈。为了解决这些问题,研究者提出了新型的注意力机制,如多查询注意力(MQA) 、分组查询注意力(GQA)和多头潜在注意力(MLA),它们通过不同的优化策略提升了Transformer的效率。
本文将详细探讨这些注意力机制的原理、公式推导、局限性,并进行对比分析,帮助大家理解它们的特点及适用场景。
1. 多头注意力机制(MHA)
可参考我的以往文章:
【Transformer原理详解1】:https://blog.csdn.net/qq_52920290/article/details/157328797?spm=1001.2014.3001.5501
【Transformer原理详解2】:https://blog.csdn.net/qq_52920290/article/details/157440788?spm=1001.2014.3001.5501
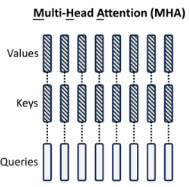
原理与公式推导
多头注意力(MHA) 是Transformer的核心模块,其目的是通过多个并行的注意力头来捕捉不同子空间的信息,从而增强模型的表达能力。
给定输入序列 X = [ x 1 , x 2 , . . . , x n ] ∈ R n × d X = [x_1, x_2, ..., x_n] \in \mathbb{R}^{n \times d} X=[x1,x2,...,xn]∈Rn×d,其中 n n n 是序列长度, d d d 是隐藏层维度。
1) 线性投影生成 Q, K, V
对于每个头 i i i,我们使用线性变换生成Query (Q) 、Key (K)和Value (V):
Q i = X W i Q , K i = X W i K , V i = X W i V Q_i = X W_i^Q, \quad K_i = X W_i^K, \quad V_i = X W_i^V Qi=XWiQ,Ki=XWiK,Vi=XWiV
2) 缩放点积注意力
对于每个头的注意力计算,使用缩放点积注意力:
Attention i = softmax ( Q i K i ⊤ d h ) V i \text{Attention}_i = \text{softmax}\left(\frac{Q_i K_i^\top}{\sqrt{d_h}}\right)V_i Attentioni=softmax(dh QiKi⊤)Vi
其中 d h = d h d_h = \frac{d}{h} dh=hd 是每个头的维度, h h h 是头的数量。
3) 多头拼接与输出映射
最终,将多个头的输出拼接在一起,通过线性映射得到最终的输出:
MHA ( X ) = Concat ( Attention 1 , ... , Attention h ) W O \text{MHA}(X) = \text{Concat}(\text{Attention}_1, \dots, \text{Attention}_h) W^O MHA(X)=Concat(Attention1,...,Attentionh)WO
局限性
- 计算和内存开销高 :随着序列长度和头数的增加,计算复杂度为 O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d),导致内存消耗也随之增加。
- KV缓存问题 :推理时需要缓存每个头的Key 和Value,这会显著增加显存消耗。
2. 多查询注意力(MQA)
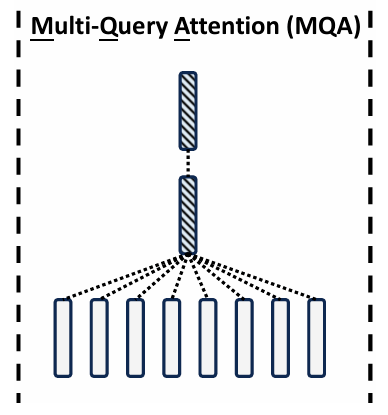
原理与公式推导
多查询注意力(MQA)通过将多个注意力头的查询共享同一组Key 和Value,从而减少计算和内存开销。
1) 查询保持独立
每个注意力头独立生成Query ,但共享相同的Key 和Value:
Q i = X W i Q Q_i = X W_i^Q Qi=XWiQ
2) 共享Key和Value
所有的头共享同一组Key 和Value:
K = X W K , V = X W V K = X W^K, \quad V = X W^V K=XWK,V=XWV
3) 注意力计算
每个头的注意力计算如下:
Attention i = softmax ( Q i K ⊤ d h ) V \text{Attention}_i = \text{softmax}\left(\frac{Q_i K^\top}{\sqrt{d_h}}\right)V Attentioni=softmax(dh QiK⊤)V
局限性
- 表达能力下降 :由于所有头共享同一组Key 和Value,不同头之间的表达差异性降低,可能导致性能下降。
- 对长序列任务不适应:在需要捕捉长距离依赖的任务中,MQA的效果不如MHA。
3. 分组查询注意力(GQA)
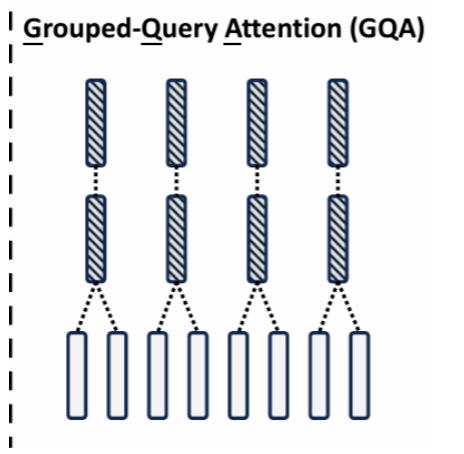
原理与公式推导
分组查询注意力(GQA)是MHA 和MQA 的折衷方法,通过将头分组,每个组共享同一组Key 和Value,但组内的头仍然独立计算。
1) 分组计算
假设有 h h h 个头,分为 g g g 组,每组包含 h / g h/g h/g 个头:
K ( j ) = X W j K , V ( j ) = X W j V K^{(j)} = X W_j^K, \quad V^{(j)} = X W_j^V K(j)=XWjK,V(j)=XWjV
组内每个头的注意力计算:
Attention i = softmax ( Q i K ( j ) ⊤ d h ) V ( j ) \text{Attention}_i = \text{softmax}\left(\frac{Q_i K^{(j)\top}}{\sqrt{d_h}}\right)V^{(j)} Attentioni=softmax(dh QiK(j)⊤)V(j)
局限性
- 超参数依赖 :分组数 g g g 的选择对性能有较大影响,需要调参。
- 复杂度增加:分组数的选择增加了模型的调参复杂度。
4. 多头潜在注意力(MLA)
为了更好地理解MLA(Multi-Head Latent Attention) ,我们将详细讲解其公式推导 和原理,并结合相关图示对其进行全面的说明。
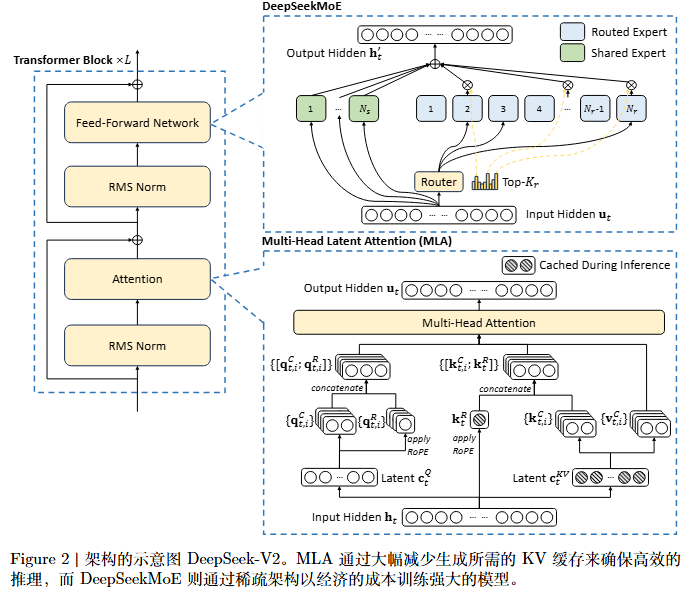
【参考原文】:DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model
arxiv: https://arxiv.org/abs/2405.04434
4.1 MLA原理概述
MLA 是一种通过低秩压缩(Low-Rank Compression)来优化传统多头注意力(MHA )机制的方案。其主要目标是减少 Key 和Value 在注意力计算中的内存开销,同时保持模型的表达能力。它通过引入潜在空间(Latent Space)来对输入的Query (Q) 、Key (K)和Value (V) 进行低秩压缩,从而减小计算和内存负担。
关键步骤:
- 低秩压缩 :将Key 和Value 映射到低秩潜在空间,对Query也做了同样处理。
- 位置编码(RoPE) :使用RoPE进行位置编码,以便更好地捕捉输入序列的顺序信息。
- 多头并行计算:通过多个并行的注意力头来增强模型的表达能力。
- 缓存机制:在推理阶段缓存计算结果,以减少计算复杂度。
4.2 公式推导
4.2.1 低秩压缩
假设输入为一个隐藏状态 h t ∈ R n × d h_t \in \mathbb{R}^{n \times d} ht∈Rn×d,其中 n n n 是序列长度, d d d 是每个词向量的维度。
在MHA 中,多个注意力头使用不同的Query 、Key 和Value进行计算:
Q i = X W i Q , K i = X W i K , V i = X W i V Q_i = X W_i^Q, \quad K_i = X W_i^K, \quad V_i = X W_i^V Qi=XWiQ,Ki=XWiK,Vi=XWiV
其中, W i Q W_i^Q WiQ, W i K W_i^K WiK, W i V W_i^V WiV 是每个注意力头的参数矩阵。
在MLA 中,为了节省内存和计算资源,我们使用低秩压缩 来减少Key 和Value的维度。
1) 低秩映射
将原始的Key 和Value映射到低秩潜在空间:
Q t = X W Q , K t = X W K , V t = X W V Q_t = X W^Q, \quad K_t = X W^K, \quad V_t = X W^V Qt=XWQ,Kt=XWK,Vt=XWV
通过低秩分解,我们将原始的Key 和Value映射到潜在空间:
Q t latent = f ( Q t ) , K t latent = f ( K t ) , V t latent = f ( V t ) Q_t^{\text{latent}} = f(Q_t), \quad K_t^{\text{latent}} = f(K_t), \quad V_t^{\text{latent}} = f(V_t) Qtlatent=f(Qt),Ktlatent=f(Kt),Vtlatent=f(Vt)
其中, f ( ⋅ ) f(\cdot) f(⋅) 表示低秩压缩操作,通常通过矩阵分解 或因式分解方法进行。
这样,通过压缩后的 Q t Q_t Qt, K t K_t Kt, 和 V t V_t Vt,我们可以在一个较低维度的潜在空间内进行计算,从而降低了计算和内存的开销。
2) 注意力计算
计算每个头的注意力时,使用低秩压缩后的 Q t Q_t Qt、 K t K_t Kt 和 V t V_t Vt 来计算注意力权重。注意力的计算公式为:
Attention i = softmax ( Q t latent K t latent ⊤ d h ) V t latent \text{Attention}_i = \text{softmax}\left(\frac{Q_t^{\text{latent}} K_t^{\text{latent}\top}}{\sqrt{d_h}}\right)V_t^{\text{latent}} Attentioni=softmax(dh QtlatentKtlatent⊤)Vtlatent
其中, d h d_h dh 是每个头的维度,通常为 d h = d h d_h = \frac{d}{h} dh=hd, h h h 是头数。
最终的输出通过多个头进行拼接(Concatenation)并通过线性变换得到:
MLA ( X ) = Concat ( Attention 1 , ... , Attention h ) W O \text{MLA}(X) = \text{Concat}(\text{Attention}_1, \dots, \text{Attention}_h) W^O MLA(X)=Concat(Attention1,...,Attentionh)WO
4.2.2 位置编码(RoPE)
在MLA中,我们使用**RoPE(Rotary Positional Encoding)**来处理输入的顺序信息。RoPE方法通过旋转的方式嵌入位置信息,使得模型能够更好地理解序列中的相对位置。
RoPE应用
在图示中,RoPE 被应用于压缩后的Query 和Key/Value,以保持位置编码的同时避免内存开销过大。RoPE的应用公式为:
Q t latent = RoPE ( Q t latent ) , K t latent = RoPE ( K t latent ) Q_t^{\text{latent}} = \text{RoPE}(Q_t^{\text{latent}}), \quad K_t^{\text{latent}} = \text{RoPE}(K_t^{\text{latent}}) Qtlatent=RoPE(Qtlatent),Ktlatent=RoPE(Ktlatent)
这使得 Q t Q_t Qt 和 K t K_t Kt 在潜在空间中不仅包含语义信息,还能有效编码顺序信息。
4.3 MLA的工作流程
- 输入(Hidden State) :输入的隐藏状态 h t h_t ht 通过线性映射得到Query (Q) 、Key (K)和Value (V)。
- 低秩压缩 :对Q 、K 和V 进行低秩压缩,得到Latent ( Q t Q_t Qt )和 Latent ( K t V t K_tV_t KtVt )。
- RoPE :将旋转位置编码(RoPE)应用于压缩后的 Q t Q_t Qt 和 K t K_t Kt。
- 注意力计算 :使用低秩压缩后的 Q t Q_t Qt 和 K t K_t Kt 进行注意力计算。
- 多头拼接:将多个注意力头的结果拼接起来,并通过一个线性变换输出最终结果。
4.4 MLA与MHA的对比
| 特性 | MHA(多头注意力) | MLA(多头潜在注意力) |
|---|---|---|
| Key/Value | 每个头有独立的Key/Value | 所有头共享低秩压缩后的Key/Value |
| 内存消耗 | 高 | 低(通过低秩压缩) |
| 计算复杂度 | O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d) | O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d)(但低秩计算更高效) |
| 表达能力 | 强 | 接近MHA,但略有压缩损失 |
| 适用场景 | 适用于计算资源丰富的任务 | 适用于长序列任务和显存有限的任务 |
4.5 局限性
- 压缩效果有限:过度压缩可能丧失一些表达能力,影响性能。
- 实现复杂:相较于MHA,MLA需要更复杂的实现和低秩压缩过程。
5. 对比表
| 机制 | 意图 | Key/Value特性 | 参数&内存开销 | 表达能力 | 计算复杂度 | 局限性 |
|---|---|---|---|---|---|---|
| MHA | 多子空间并行建模 | 每头独立 | 高(与头数正比) | 最强 | O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d) | 内存&计算高 |
| MQA | 极致内存压缩 | 所有头共享K/V | 极低 | 弱 | O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d) | 信息表达不足 |
| GQA | 性能/效率折中 | 每组共享K/V | 中等 | 较好 | O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d) | 分组超参敏感 |
| MLA | 低秩压缩&长序列优化 | 压缩潜变量空间 | 低(潜维度控制) | 接近MHA | O ( n 2 ⋅ d ) O(n^2 \cdot d) O(n2⋅d)(低秩) | 结构复杂 |
6. 总结
在实际应用中,选择合适的注意力机制取决于任务的计算资源、内存需求以及表达能力要求。MHA 适用于需要强表达能力和资源充足的任务,MQA 则适用于内存受限的场景,GQA 提供了计算与内存的平衡,而MLA则在长序列任务和显存紧张的环境中提供了最优的性能。
MLA 在长序列任务中提供了显著的优势,尤其在内存受限的情况下,通过低秩压缩 和潜在空间计算 显著减少了显存的使用,并提高了计算效率。如果你正在开发一个需要高效处理长序列的模型,或者在显存有限的情况下进行推理,MLA将是一个值得考虑的优化方案。
版权声明:本文为CSDN博主原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。