4.3 均匀非对称耦合线
对称耦合线代表了一类非常有用的耦合线,但也有限制。在许多实际情况下,使用非对称耦合线设计组件可能更有用,甚至是必要的。例如,使用非对称耦合线的前向波定向耦合器 的带宽 比使用对称耦合线形成的耦合器更大。此外,在某些情况下,其中一条耦合线的终端阻抗可能与其他线不同。那么,选择两条具有不同特性阻抗的耦合线可能更有用。
本节描述了非对称耦合准 TEM 模式线的分析和设计。首先定义了非对称耦合线的**正常模式参数。结果表明,表征非对称耦合线需要六个独立参数。**推导了正常模式参数(即特性阻抗、相速度)和线路参数(即单位长度电感、电容)之间的关系。因为对称线是非对称耦合线的一种特殊情况,以下各节给出的各种表达式也可用于对称耦合线。文献 [5] 中对非对称耦合线进行了简洁而精彩的分析,这构成了以下分析的主要基础。
4.3.1 非对称耦合线
一组两条耦合线可以支持两个基本的独立传播模式(称为正常模式)。对于非对称耦合线,**两种正常传播模式被称为 c 模式和 π \pi π 模式。**严格来说,由两条耦合线组成的结构可以支持四种独立的传播模式:两种向后传播,两种向前传播。然而,向后传播模式的特性(相速度和特性阻抗)与对应的前向传播模式相同。c 模式是类偶模,而 π \pi π 模式是类奇模。
c 模式
图 4.6 显示了两条均匀耦合的准 TEM 模式非对称传输线。这里做出准 TEM 模式的假设,因为与非 TEM 模式传输线相比,在这种情况下可以定义唯一的电压和电流。设非对称耦合线上的电压和电流波如图所示。线 1 和线 2 上的前向传播电压 波分别表示为V 1 c + e − γ c z V_{1c}^{+}e^{-\gamma_{c}z} V1c+e−γcz 和 V 2 c + e − γ c z V_{2c}^{+}e^{-\gamma_{c}z} V2c+e−γcz ;相应的电流波分别表示为 I 1 c + e − γ c z I_{1c}^{+}e^{-\gamma_{c}z} I1c+e−γcz 和 I 2 c + e − γ c z I_{2c}^{+}e^{-\gamma_{c}z} I2c+e−γcz 。类似地, V 1 c − e γ c z V_{1c}^{-}e^{\gamma_{c}z} V1c−eγcz 和 V 2 c − e γ c z V_{2c}^{-}e^{\gamma_{c}z} V2c−eγcz、 I 1 c − e γ c z I_{1c}^{-}e^{\gamma_{c}z} I1c−eγcz 和 I 2 c − e γ c z I_{2c}^{-}e^{\gamma_{c}z} I2c−eγcz 表示后向传播模式的相应量。
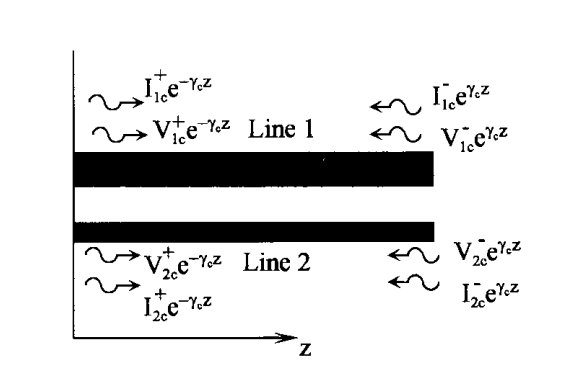
图 4.6 非对称耦合线上 c 模式的电压和电流波。
线 1 的特性阻抗(在线 2 存在的情况下)可以定义为
Z c 1 = V 1 c + I 1 c + = V 1 c − I 1 c − ( 4.61 ) Z_{c1}=\frac{V_{1c}^{+}}{I_{1c}^{+}}=\frac{V_{1c}^{-}}{I_{1c}^{-}}\qquad(4.61) Zc1=I1c+V1c+=I1c−V1c−(4.61)
类似地,对于同一模式,线 2 的特性阻抗(在线 1 存在的情况下)可以定义为
Z c 2 = V 2 c + I 2 c + = V 2 c − I 2 c − ( 4.62 ) Z_{c2}=\frac{V_{2c}^{+}}{I_{2c}^{+}}=\frac{V_{2c}^{-}}{I_{2c}^{-}}\qquad(4.62) Zc2=I2c+V2c+=I2c−V2c−(4.62)
此外,设两条线上电压的比率由参数 R c R_{c} Rc 定义如下:
R c = V 2 c + V 1 c + = V 2 c − V 1 c − R_{c}=\frac{V_{2c}^{+}}{V_{1c}^{+}}=\frac{V_{2c}^{-}}{V_{1c}^{-}} Rc=V1c+V2c+=V1c−V2c−
因此,c 模式由四个参数表征:γ c \gamma_{c} γc,模式的传播常数; Z c 1 Z_{c1} Zc1 和 Z c 2 Z_{c2} Zc2,分别是线 1 和线 2 的特性阻抗;以及 R c R_{c} Rc,两条线上的电压比率。
π \pi π 模式
与 c 模式类似, π \pi π 模式也由四个参数表征:γ π \gamma_{\pi} γπ,模式的传播常数; Z π 1 Z_{\pi 1} Zπ1 和 Z π 2 Z_{\pi 2} Zπ2,分别是线 1 和线 2 的特性阻抗;以及 R π R_{\pi} Rπ,两条线上的电压比率。
上述八个量(c 和 π \pi π 模式各四个)中,只有六个是独立的。两种模式的电流和电压满足以下关系:
在无耗、互易的耦合传输线系统中,两个正常模式(c 和 π)的功率流是彼此独立的。这种独立性在数学上表现为模式电压与模式电流之间满足特定的正交条件。
从去耦后的传输线方程出发:
d d z [ V 1 V 2 ] = − j ω [ L 1 L m L m L 2 ] [ I 1 I 2 ] \frac{d}{dz}\begin{bmatrix} V_1 \\ V_2 \end{bmatrix} = -j\omega \begin{bmatrix} L_1 & L_m \\ L_m & L_2 \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} dzd[V1V2]=−jω[L1LmLmL2][I1I2]
d d z [ I 1 I 2 ] = − j ω [ C 1 − C m − C m C 2 ] [ V 1 V 2 ] \frac{d}{dz}\begin{bmatrix} I_1 \\ I_2 \end{bmatrix} = -j\omega \begin{bmatrix} C_1 & -C_m \\ -C_m & C_2 \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} dzd[I1I2]=−jω[C1−Cm−CmC2][V1V2]
假设解的形式为 e − γ z e^{-\gamma z} e−γz,可将其转化为特征值问题。对于两个不同的模式( γ c ≠ γ π \gamma_c \neq \gamma_\pi γc=γπ),其对应的电压-电流特征向量满足由系统矩阵的对称性(源于互易性和无耗性)所决定的正交关系。
一个关键的正交关系形式为:一个模式的电压向量与另一个模式的电流向量的点积为零 。即:
V 1 c I 1 π + V 2 c I 2 π = 0 V_{1c} I_{1\pi} + V_{2c} I_{2\pi} = 0 V1cI1π+V2cI2π=0
将电压比 R c = V 2 c / V 1 c R_c = V_{2c}/V_{1c} Rc=V2c/V1c 代入上式,可得:
V 1 c I 1 π + R c V 1 c I 2 π = 0 ⇒ I 1 π + R c I 2 π = 0 V_{1c} I_{1\pi} + R_c V_{1c} I_{2\pi} = 0 \quad \Rightarrow \quad I_{1\pi} + R_c I_{2\pi} = 0 V1cI1π+RcV1cI2π=0⇒I1π+RcI2π=0
于是得到:
R c = V 2 c ± V 1 c ± = − I 1 π ± I 2 π ± R_c =\frac{V_{2c}^{\pm}}{V_{1c}^{\pm}} = -\frac{I^{\pm}{1\pi}}{I^{\pm}{2\pi}} Rc=V1c±V2c±=−I2π±I1π±
R c = V 2 c + V 1 c + = V 2 c − V 1 c − = − I 1 π + I 2 π + = − I 1 π − I 2 π − ( 4.63 ) R_{c}=\frac{V_{2c}^{+}}{V_{1c}^{+}}=\frac{V_{2c}^{-}}{V_{1c}^{-}}=-\frac{I_{1\pi}^{+}}{I_{2\pi}^{+}}=-\frac{I_{1\pi}^{-}}{I_{2\pi}^{-}}\qquad(4.63) Rc=V1c+V2c+=V1c−V2c−=−I2π+I1π+=−I2π−I1π−(4.63)
从该式可以看出:c 模式的电压比 R c R_c Rc 完全由 π 模式的电流比决定。
同样的让 π \pi π模电压乘以C模电流
V 1 π I 1 c + V 2 π I 2 c = 0 V_{1\pi} I_{1c} + V_{2\pi} I_{2c} = 0 V1πI1c+V2πI2c=0
将电压比 R π = V 2 π V 1 π R_{\pi}=\dfrac{V_{2\pi}^{}}{V_{1\pi}^{}} Rπ=V1πV2π 代入上式,可得:
V 1 π I 1 c + R π V 1 π I 2 c = 0 = 0 ⇒ I 1 c + R π I 2 c = 0 V_{1\pi} I_{1c} +R_{\pi} V_{1\pi} I_{2c} = 0= 0 \quad \Rightarrow \quad I_{1c} + R_{\pi} I_{2c} = 0 V1πI1c+RπV1πI2c=0=0⇒I1c+RπI2c=0
R π = V 2 π + V 1 π + = V 2 π − V 1 π − = − I 1 c + I 2 c + = − I 1 c − I 2 c − ( 4.64 ) R_{\pi}=\frac{V_{2\pi}^{+}}{V_{1\pi}^{+}}=\frac{V_{2\pi}^{-}}{V_{1\pi}^{-}}=-\frac{I_{1c}^{+}}{I_{2c}^{+}}=-\frac{I_{1c}^{-}}{I_{2c}^{-}}\qquad(4.64) Rπ=V1π+V2π+=V1π−V2π−=−I2c+I1c+=−I2c−I1c−(4.64)
π 模式的电压比 R π R_\pi Rπ 完全由 c 模式的电流比决定。
我们想得到特性阻抗 Z c 1 Z_{c1} Zc1、 Z c 2 Z_{c2} Zc2、 Z π 1 Z_{\pi 1} Zπ1 和 Z π 2 Z_{\pi 2} Zπ2 与比率参数 R c R_{c} Rc 和 R π R_{\pi} Rπ 之间的关系。根据定义,线1和线2在c模式下的特性阻抗为:
Z c 1 = V 1 c + I 1 c + , Z c 2 = V 2 c + I 2 c + Z_{c1} = \frac{V_{1c}^+}{I_{1c}^+}, \quad Z_{c2} = \frac{V_{2c}^+}{I_{2c}^+} Zc1=I1c+V1c+,Zc2=I2c+V2c+
类似地,在π模式下:
Z π 1 = V 1 π + I 1 π + , Z π 2 = V 2 π + I 2 π + Z_{\pi1} = \frac{V_{1\pi}^+}{I_{1\pi}^+}, \quad Z_{\pi2} = \frac{V_{2\pi}^+}{I_{2\pi}^+} Zπ1=I1π+V1π+,Zπ2=I2π+V2π+
对于c模式,阻抗比为:
Z c 2 Z c 1 = V 2 c + / I 2 c + V 1 c + / I 1 c + = ( V 2 c + V 1 c + ) ( I 1 c + I 2 c + ) \frac{Z_{c2}}{Z_{c1}} = \frac{V_{2c}^+ / I_{2c}^+}{V_{1c}^+ / I_{1c}^+} = \left( \frac{V_{2c}^+}{V_{1c}^+} \right) \left( \frac{I_{1c}^+}{I_{2c}^+} \right) Zc1Zc2=V1c+/I1c+V2c+/I2c+=(V1c+V2c+)(I2c+I1c+)
根据已知条件, V 2 c + V 1 c + = R c \frac{V_{2c}^+}{V_{1c}^+} = R_c V1c+V2c+=Rc,并且由正交性关系 R π = − I 1 c + I 2 c + R_\pi = -\frac{I_{1c}^+}{I_{2c}^+} Rπ=−I2c+I1c+
将上述结果代入第2步的公式:
Z c 2 Z c 1 = R c ⋅ ( − R π ) = − R c R π (A) \frac{Z_{c2}}{Z_{c1}} = R_c \cdot (-R_\pi) = -R_c R_\pi \qquad \text{(A)} Zc1Zc2=Rc⋅(−Rπ)=−RcRπ(A)
对于π模式,阻抗比为:
Z π 2 Z π 1 = V 2 π + / I 2 π + V 1 π + / I 1 π + = ( V 2 π + V 1 π + ) ( I 1 π + I 2 π + ) \frac{Z_{\pi2}}{Z_{\pi1}} = \frac{V_{2\pi}^+ / I_{2\pi}^+}{V_{1\pi}^+ / I_{1\pi}^+} = \left( \frac{V_{2\pi}^+}{V_{1\pi}^+} \right) \left( \frac{I_{1\pi}^+}{I_{2\pi}^+} \right) Zπ1Zπ2=V1π+/I1π+V2π+/I2π+=(V1π+V2π+)(I2π+I1π+)
根据已知条件, V 2 π + V 1 π + = R π \dfrac{V_{2\pi}^+}{V_{1\pi}^+} = R_\pi V1π+V2π+=Rπ,并且由正交性关系 R c = − I 1 π + I 2 π + R_c = -\dfrac{I_{1\pi}^+}{I_{2\pi}^+} Rc=−I2π+I1π+,将上述结果代入第4步的公式:
Z π 2 Z π 1 = R π ⋅ ( − R c ) = − R c R π (B) \frac{Z_{\pi2}}{Z_{\pi1}} = R_\pi \cdot (-R_c) = -R_c R_\pi \qquad \text{(B)} Zπ1Zπ2=Rπ⋅(−Rc)=−RcRπ(B)
由等式(A)和(B)可知,c模式和π模式的特性阻抗比相等,且都等于 − R c R π -R_c R_\pi −RcRπ。因此:
Z c 2 Z c 1 = Z π 2 Z π 1 = − R c R π ( 4.65 ) \frac{Z_{c2}}{Z_{c1}}=\frac{Z_{\pi 2}}{Z_{\pi 1}}=-R_{c}R_{\pi}\qquad(4.65) Zc1Zc2=Zπ1Zπ2=−RcRπ(4.65)
因此,**表征非对称耦合线总共需要六个量(即 γ c \gamma_{c} γc、 γ π \gamma_{\pi} γπ、 Z c 1 Z_{c1} Zc1 [或 Z c 2 Z_{c2} Zc2]、 Z π 1 Z_{\pi 1} Zπ1 [或 Z π 2 Z_{\pi 2} Zπ2]、 R c R_{c} Rc 和 R π R_{\pi} Rπ)。**不需要同时指定 Z c 1 Z_{c1} Zc1 和 Z c 2 Z_{c2} Zc2,因为它们通过 (4.65) 相关 。 Z π 1 Z_{\pi 1} Zπ1 和 Z π 2 Z_{\pi 2} Zπ2 也是如此。另一方面,对称耦合线完全由四个参数表征:任意一条线的偶模和奇模特性阻抗(因为两条线相同)以及偶模和奇模相位常数。对于对称耦合线, R c = 1 R_{c}=1 Rc=1 和 R π = − 1 R_{\pi}=-1 Rπ=−1。