无向图的连通性之割点/边，点/边双连通分量

我将依托几道经典例题来讲解

割点/边

题目描述

具体题干我就不放了，顾名思义就是找割点/边。

割点AC代码

cpp 复制代码

#include <bits/stdc++.h>
    using namespace std;
    const int maxn = 1e5 + 5;

    int n, m, dfn[maxn], low[maxn], ts;
    bool cut[maxn];
    vector<int> g[maxn];

    void tarjan(int u) {
        dfn[u] = low[u] = ++ts;
        int cnt = 0;
        for (auto v : g[u]) {
            if (!dfn[v]) { // 前向边，v是u在搜索树上的子节点
                cnt++;
                tarjan(v);
                low[u] = min(low[u], low[v]);
                if (low[v] == dfn[u] && u != 1) {
                    cut[u] = true;
                }
            }
            else { // v是u在搜索树上的祖先节点
                low[u] = min(low[u], dfn[v]);
            }
        }
        if (u == 1 && cnt >= 2)
            cut[u] = true;
    }
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0, u, v; i < m; i++) {
        scanf("%d%d", &u, &v);
        g[u].push_back(v);
        g[v].push_back(u);
    }
    tarjan(1);
    bool flag = false;
    for (int i = 1; i <= n; i++) {
        if (cut[i]) {
            flag = true;
            printf("%d\n", i);
        }
    }
    if (!flag)
        puts("no");
    return 0;
}

逐步讲解

其实割点很好理解，我们以下图为例，3和5是割点。

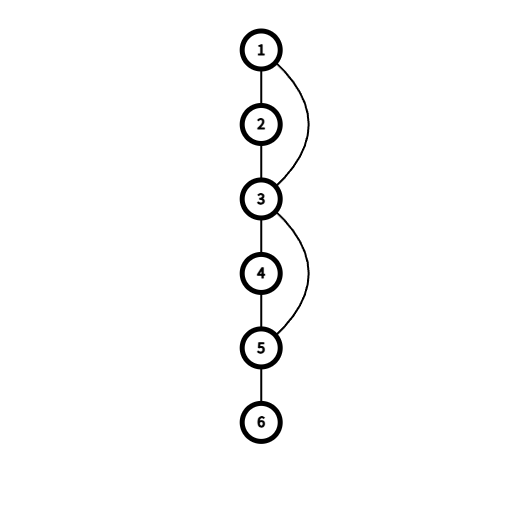图1-1

显而易见，在一个连通图中如果去掉一个节点a后破坏了原图的连通性，那么节点a就是割点。

那割点有什么样的特征呢？我们可以看出3和5都是一个环的一部分，那么这时候就有人问了，如果上图中3-5这条边不存在，5仍然是割点呀，确实，但是由于是无向图，5可以到达4和6，同时4和6也可以到达5，那这不就说明4和5成环，5和6成环吗，所以我们得到第一个性质：割点是环的一部分。

那么这条性质有什么用呢？

如果我们把题目给出的图变成一颗无向树（如上图）我们就可以发现割点所在的环是通过向下遍历若干步后再向上遍历一步到达割点的。那是不是如果满足这个条件就是割点了呢？非也，如果我们给上图加一条边2-4，得到下图。

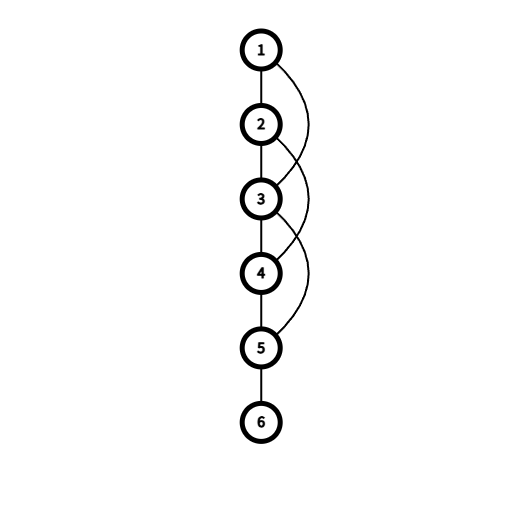图1-2

可以发现在图1-2中2和5都不再是割点，因为去掉2或5后原图的连通性并没有被破坏。所以我们可以知道一个点想要是割点，必须满足存在向下若干步后向上一步到达它本身的路径并且它下方的（之后被遍历的）节点不存在一条向上的路到达比它还高（更先被遍历）的点。

代码实现：

cpp 复制代码

    void tarjan(int u) {
        dfn[u] = low[u] = ++ts;
        int cnt = 0;
        for (auto v : g[u]) {
            if (!dfn[v]) { // 前向边，v是u在搜索树上的子节点
                cnt++;
                tarjan(v);
                low[u] = min(low[u], low[v]);
                if (low[v] == dfn[u] && u != 1) {
                    cut[u] = true;
                }
            }
            else { // v是u在搜索树上的祖先节点
                low[u] = min(low[u], dfn[v]);
            }
        }
        if (u == 1 && cnt >= 2)
            cut[u] = true;
    }

其实整个算法的实现都在这一个函数，具体的实现分为两部分，前向也就是向下（dfn[v]==0代表没有被遍历过），后向也就是向上（被遍历过），如果遍历到了向下的节点，那么继续dfs，如果遍历到了向上的节点那么更新当前节点的low，之后非常有意思，节点会根据dfs的顺序不断返回，每返回一次，当前节点都会被下面的节点更新low（保证low最大，原因已分析过），之后再判断当前节点有没有一条来自下面的向上节点到达当前节点，如果是他就是割点。

再者就是一个根节点的处理（根节点无法向上遍历），所以我们单独讨论如果根节点有超过一个儿子，那么它就是割点（不懂自己去画图）。

割边AC代码

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4 + 5, maxm = 1e5 + 5;

int n, m, dfn[maxn], low[maxn], ts;
bool cut[maxm];

struct Edge {
    int id, v; // id:边的编号，v：终点
};
vector<Edge> g[maxn];

void tarjan(int u, int pe) {
    dfn[u] = low[u] = ++ts;
    for (auto& [id, v] : g[u]) {
        if (id == pe)
            continue;
        if (!dfn[v]) {
            tarjan(v, id);
            low[u] = min(low[u], low[v]);
            if (low[v] > dfn[u])
                cut[id] = true;
        }
        else 
            low[u] = min(low[u], dfn[v]);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; i++) {
        scanf("%d%d", &u, &v);
        g[u].push_back({ i, v });
        g[v].push_back({ i, u });
    }
    tarjan(1, 0);
    bool flag = false;
    for (int i = 1; i <= m; i++) {
        if (cut[i]) {
            printf("%d\n", i);
            flag = true;
        }
    }
    if (!flag)
        puts("no");
    return 0;
}

逐步讲解

逐步讲解，割边的代码部分和割点很类似，逻辑上稍有不同

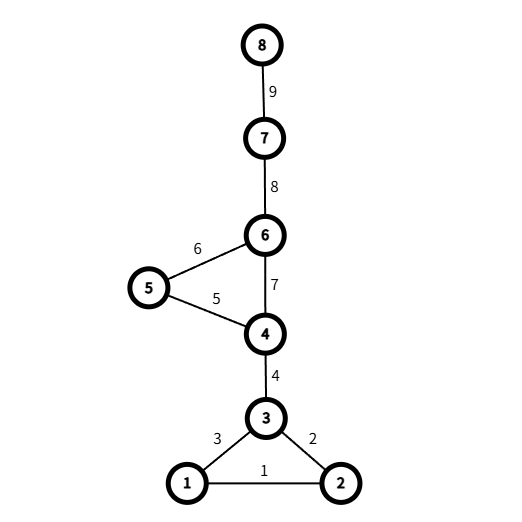图2-1

如上图边4，8，9是割边，理由类比割点。

我们会发现如果一个节点a不存在向下若干步再向上一步到达a之上的通路（不能遍历父节点），那么这个点就是割边，割边的判断条件比割点复杂，原因就在于对于无向图来说，割边割的是一条无向边（来回两条有向边），所以我们不能遍历父节点（同一条边走两次相当于有两条边，但实际只有一条），因为如果能遍历父节点，算法会误以为子树 v 有路能回 u，从而认为这条边不是桥。

代码如下：

cpp 复制代码

struct Edge {
    int id, v; // id:边的编号，v：终点
};
vector<Edge> g[maxn];

void tarjan(int u, int pe) {
    dfn[u] = low[u] = ++ts;
    for (auto& [id, v] : g[u]) {
        if (id == pe)
            continue;
        if (!dfn[v]) {
            tarjan(v, id);
            low[u] = min(low[u], low[v]);
            if (low[v] > dfn[u])
                cut[id] = true;
        }
        else 
            low[u] = min(low[u], dfn[v]);
    }
}

这里pe代表的是从那条边到达的当前节点u，如果你接下来要遍历的边id就是你来的边pe，那么说明你同一条边走了两次，所以要continue。其他的实现逻辑上文已经讲过。

点/边双连通分量

题目描述

P8435 【模板】点双连通分量 - 洛谷 P8436 【模板】边双连通分量 - 洛谷

点双连通分量AC代码

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 5;

int n, m, dfn[maxn], low[maxn], ts, bcc, rt;
vector<int> g[maxn], vec[maxn];
stack<int> stk;

void tarjan(int u) {
    dfn[u] = low[u] = ++ts;
    stk.push(u);
    for (auto v : g[u]) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
            if (low[v] == dfn[u]) {
                bcc++;
                int x;
                do {
                    x = stk.top();
                    stk.pop();
                    vec[bcc].push_back(x);
                } while (x != v);
                vec[bcc].push_back(u);
            }
        }
        else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0, u, v; i < m; i++) {
        scanf("%d%d", &u, &v);
        if (u == v) // 自环
            continue;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) {
            if (g[i].size() == 0) {
                bcc++;
                vec[bcc].push_back(i);
            }
            else {
                while (!stk.empty())
                    stk.pop();
                rt = i;
                tarjan(i);
            }
        }
    }
    printf("%d\n", bcc);
    for (int i = 1; i <= bcc; i++) {
        printf("%d", (int)vec[i].size());
        for (auto u : vec[i])
            printf(" %d", u);
        puts("");
    }
    return 0;
}

逐步讲解

所谓点双连通分量就是一个连通图去掉任意一个点都不改变原图的连通性（也就是没有割点），换句话说，我们只要找到一个连通图内所有的割点并去掉所有割点，之后形成的若干个连通分量都是点双连通分量，

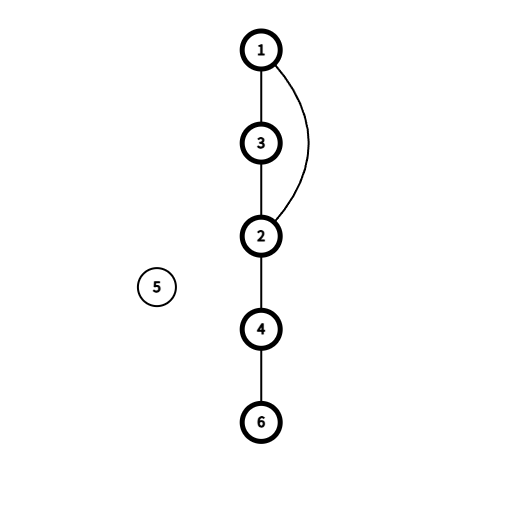图3

如图3

它的点双连通分量分别是

6 4

4 2

3 2 1

我们可以发现，点双连通分量确实是被割点分开的，那我们要做的就很简单了，在dfs向上遍历的过程中，如果发现割点，那么在这个割点之下及它本身就一定是点双连通分量，否则他们就会被分开。具体代码如下：

cpp 复制代码

stack<int> stk;

void tarjan(int u) {
    dfn[u] = low[u] = ++ts;
    stk.push(u);
    for (auto v : g[u]) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
            if (low[v] == dfn[u]) {
                bcc++;
                int x;
                do {
                    x = stk.top();
                    stk.pop();
                    vec[bcc].push_back(x);
                } while (x != v);
                vec[bcc].push_back(u);
            }
        }
        else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

我们用栈来实现上述逻辑，当发现割点时把割点及割点前的节点全部push进答案，割点前的节点全部pop，注意不能pop割点，因为割点也一定是另一个点双连通分量的节点，毕竟能割开就代表本来相连，另外注意题目没有说是连通图所以要遍历所有节点，每发现一个新的连通分量要重新选定根节点。

cpp 复制代码

    for (int i = 1; i <= n; i++) {
        if (!dfn[i]) {
            if (g[i].size() == 0) {
                bcc++;
                vec[bcc].push_back(i);
            }
            else {
                while (!stk.empty())
                    stk.pop();
                rt = i;
                tarjan(i);
            }
        }
    }

其他的地方与上文雷同。

边双连通分量AC代码

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 5, maxm = 2e6 + 5;

int n, m, dfn[maxn], low[maxn], ts, rt, bcc;
vector<int> g[maxn];
stack<int> stk;
vector<int> vec[maxn];

void tarjan(int u, int p) {
    dfn[u] = low[u] = ++ts;
    stk.push(u);
    int cnt = 0;
    for (auto v : g[u]) {
        if (v == p) {
            cnt++;
            if (cnt == 1) continue;
        }
        if (!dfn[v]) {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
        }
        else
            low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u] || u == rt) {
        bcc++;
        int x;
        do {
            x = stk.top();
            stk.pop();
            vec[bcc].push_back(x);
        } while (x != u);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0, u, v; i < m; i++) {
        scanf("%d%d", &u, &v);
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            rt = i, tarjan(i, 0);
    printf("%d\n", bcc);
    for (int i = 1; i <= bcc; i++) {
        printf("%d", (int)vec[i].size());
        for (auto u : vec[i])
            printf(" %d", u);
        puts("");
    }
    return 0;
}

逐步讲解

边双连通分量和点双连通分量类似，就是如果遇到割边就把割边之下的节点全部push+pop。

版本答案：圆方树

cpp 复制代码

# AT_abc318_g [ABC318G] Typical Path Problem

## 题目描述

给出一个有 $n$ 个顶点和 $m$ 条边的无向连通图 $G$，没有重边和自环。

顶点的编号为 $1 \sim n$，边的编号为 $1 \sim m$，第 $i$ 条边连接顶点 $u_i$ 和 $v_i$。

给出图上三个不同的顶点 $A,B,C$。判断是否有从点 $A$ 经过点 $B$ 到点 $C$ 的简单路径。

简单路径指路径上的点互不相同，即不重复经过同一个点。

## 输入格式

第一行有两个整数 $n,m$。  
第二行有三个整数 $A,B,C$。  
接下来 $m$ 行，每行两个整数 $u_i$ 和 $v_i$。

## 输出格式

输出一行 `Yes` 或 `No`。

什么是圆方树呢？那就是一个方点（点连通分量）有多个子儿子（连通分量节点），如果你把图转化成圆方树的形式后，你会发现这是一个连通树，因为一个割点连接两个方点（见上文），那么就大致会有这种情况（其余情况雷同）：

1，a所在方点--b所在方点--c所在方点

这种情况毋庸置疑符合题意。

2，a所在方点--c所在方点--b所在方点

因为短线是单向通道只能走一次（简单路径），所以不符合题意

3，c所在方点--a所在方点--b所在方点

同理不符合题意

4，ab（先a后b）所在方点--c所在方点

类比1，符合题意

5，ac所在方点--b所在方点

类比2，不符合题意

所以我们可以知道不管a,b,c是否在同一个点双连通分量，只要在圆方树中dfs逆序遍历c直到a（我们可以设为根节点）的过程中遍历到b就符合题意（如果从a开始遍历会因为有很多不同的分支而找不到c）。

今天就到这里吧，累了