LeetCode-Hot100 30.两两交换链表中的节点

【详解】两两交换链表中的节点（递归 + 迭代双解法）

在链表相关的算法题中，"两两交换链表中的节点" 是一道经典的基础题，既考察对链表结构的理解，也能锻炼递归和迭代两种核心编程思维。本文会从问题分析入手，分别讲解递归解法 和迭代解法的思路、实现细节，以及关键边界处理，帮助新手彻底吃透这道题。

一、问题描述

题目要求

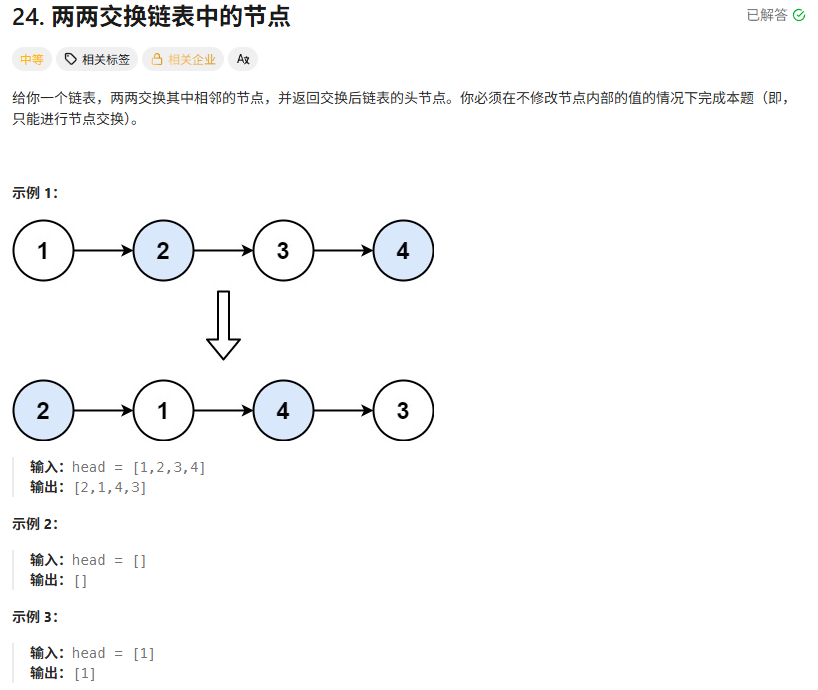
给定一个单链表，两两交换其中相邻的节点，并返回交换后的链表。注意：不能只是单纯改变节点内部的值，而是需要实际的节点交换。

示例

• 输入：1->2->3->4

• 输出：2->1->4->3

• 输入：1->2->3

• 输出：2->1->3

• 输入：1

• 输出：1

二、核心思路分析

链表的核心特点是 "单向依赖"，只能通过next指针访问后续节点。两两交换的本质是：

1. 交换相邻两个节点的指向关系；
2. 把交换后的节点与剩余链表正确拼接；
3. 处理边界情况（链表为空、链表长度为奇数、只有一个节点）。

接下来分别讲解两种解法：

三、解法一：递归解法（简洁优雅）

1. 递归思路

递归的核心是 "拆分问题 + 找终止条件"，把复杂的链表交换拆解为 "当前两个节点交换 + 剩余链表递归处理"：

• 终止条件 ：当链表为空（head == null）或只剩一个节点（head.next == null）时，无需交换，直接返回原节点；
• 递归过程 ：① 定义当前要交换的两个节点node1（头节点）、node2（头节点的下一个节点）；② 交换两个节点：让node2指向node1；③ 递归处理node2之后的剩余链表，把递归结果接在node1后面；④ 返回node2作为当前层交换后的新头节点。

2. 递归代码实现

class Solution {
    public ListNode swapPairs(ListNode head) {
        // 递归终止条件：空链表 或 只有一个节点，无需交换
        if (head == null || head.next == null) {
            return head;
        }

        // 定义当前要交换的两个节点
        ListNode node1 = head;          // 第一个节点
        ListNode node2 = head.next;     // 第二个节点
        ListNode rest = node2.next;     // 剩余链表的头节点

        // 第一步：交换当前两个节点，node2 指向 node1
        node2.next = node1;
        // 第二步：递归处理剩余链表，并把结果接在 node1 后面
        node1.next = swapPairs(rest);
        // 第三步：返回当前层交换后的新头节点（node2 取代 node1 成为新头）
        return node2;
    }
}

3. 关键细节解释

• 终止条件的必要性：如果没有终止条件，递归会无限调用，最终导致栈溢出；同时，终止条件也处理了 "链表长度为奇数" 的边界（最后一个节点无需交换）。
• 返回值的核心逻辑 ：每一层递归都返回 "交换后的新头节点（node2）"，才能让上层链表正确拼接。比如第一层递归处理1->2后，返回2作为新头，后续递归处理3->4返回4，最终拼接为2->1->4->3。
• 剩余链表的处理 ：rest = node2.next 是提前保存剩余链表的头节点，避免交换node2.next后丢失后续节点。

4. 递归执行流程（以1->2->3->4为例）

第一层递归（head=1）：
  node1=1, node2=2, rest=3
  node2.next = 1 → 2->1
  调用 swapPairs(3)
    第二层递归（head=3）：
      node1=3, node2=4, rest=null
      node2.next = 3 →4->3
      调用 swapPairs(null) → 触发终止条件，返回null
    node1.next = null →3->null
    返回 node2=4
  node1.next =4 →1->4
  返回 node2=2 → 最终结果 2->1->4->3

四、解法二：迭代解法（更贴近底层）

1. 迭代思路

迭代的核心是 "借助虚拟头节点 + 指针遍历"，避免单独处理头节点的边界问题：

• 虚拟头节点（dummy） ：统一 "交换头节点" 和 "交换中间节点" 的逻辑（比如链表1->2，直接交换头节点时，虚拟头节点能避免空指针）；
• 遍历指针（prev） ：始终指向 "待交换两个节点的前一个节点"，通过调整prev的next指针完成交换；
• 循环条件 ：只要prev后面有两个节点（prev.next != null && prev.next.next != null），就继续交换。

2. 迭代代码实现

class Solution {
    public ListNode swapPairs(ListNode head) {
       ListNode dummy = new ListNode(0, head);
        ListNode node0 = dummy, node1 = head;
        while (node1 != null && node1.next != null) {
            ListNode node2 = node1.next;
            ListNode node3 = node2.next;

            node0.next = node2;
            node2.next = node1;
            node1.next = node3;

            node0 = node1;
            node1 = node0.next;
        }

        return dummy.next;
    }
}

3. 关键细节解释

• 虚拟头节点的作用 ：如果没有虚拟头节点，交换原头节点（比如1->2）时，需要单独处理head的指向；有了虚拟头节点后，prev初始指向dummy，交换逻辑和中间节点完全一致。
• 指针保存的必要性 ：交换前必须先保存node1和node2，否则修改prev.next后会丢失这两个节点的引用。
• 循环条件 ：prev.next != null && prev.next.next != null 确保每次循环都有两个节点可交换，避免空指针异常（比如链表长度为奇数时，最后一个节点不进入循环）。
• prev 的移动 ：每次交换完成后，prev移动到node1（交换后的第二个节点），因为下一组待交换节点的前一个节点就是node1。

4. 迭代执行流程（以1->2->3->4为例）

初始状态：dummy->1->2->3->4，prev=dummy
第一次循环：
  node1=1, node2=2
  node1.next = 3 →1->3
  node2.next = 1 →2->1
  prev.next = 2 →dummy->2->1->3->4
  prev = node1 →prev=1
第二次循环：
  node1=3, node2=4
  node1.next = null →3->null
  node2.next = 3 →4->3
  prev.next = 4 →1->4->3
  prev = node1 →prev=3
循环结束（prev.next=null）
返回 dummy.next →2->1->4->3

五、两种解法对比

解法	优点	缺点	时间复杂度	空间复杂度
递归	代码简洁、逻辑清晰	递归深度大时易栈溢出	O(n)	O (n)（栈帧）
迭代	空间复杂度低、稳定	代码稍繁琐、需处理指针	O(n)	O(1)

• 适用场景：递归适合理解逻辑、快速编码；迭代适合生产环境（无栈溢出风险）。

六、常见错误与避坑指南

1. 返回值错误（递归） ：比如递归中最后返回node1而非node2，会导致链表拼接错误（比如1->2交换后返回1，结果还是1->2）。
2. 丢失剩余链表（迭代） ：交换前未保存node1/node2，直接修改指针导致后续节点丢失。
3. 边界条件未处理：比如忽略 "链表为空""链表长度为 1" 的情况，会触发空指针异常。
4. 只修改节点值 ：题目要求实际交换节点，而非仅修改val，这是典型的审题错误。

七、总结

"两两交换链表中的节点" 是链表操作的基础题，核心考点有两个：

1. 理解链表的单向指向特性，通过 "提前保存指针" 避免节点丢失；
2. 掌握递归的 "拆分 + 终止" 思维，以及迭代的 "虚拟头节点 + 指针遍历" 技巧。

递归解法的核心是 "把问题拆小，先解决当前，再递归剩余"；迭代解法的核心是 "借助虚拟头节点统一逻辑，通过指针遍历完成所有交换"。两种解法都需要重点关注边界条件（空链表、奇数长度链表），这也是链表题的通用考点。