拓扑排序（Kahn算法）

拓扑排序（Kahn算法）

拓扑排序是针对有向无环图(DAG)的排序算法,目标是得到一个节点序列 ，使图中所有有向边的起点都在终点之前 ，进而可以解决一系列依赖调度类问题（如课程先修，任务执行顺序，依赖包安装等）

一、拓扑排序的核心概念

1. 有向无环图（DAG） （Directed Acyclic Graph）
   拓扑排序的唯一适用场景 ，图中所有边都是有向的，而且不存在任何环。有环图一定没有拓扑序
2. 入度 （In-degree）
   某个节点的入度 = 指向该节点的有向边的数量（该节点的前驱依赖数）

• 例如有向边a->b，则该节点b入度+1
• 入度为 0 的节点无任何前驱依赖，可以作为拓扑排序的起始节点

3. 出度 （Out-degree）
   某个节点的出度 = 该节点出发的有向边数量

• 例如：有向边a->b、a->c，节点a的出度为2

二、拓扑排序核心原理

kahn算法是基于入度的贪心策略 ：

即反复寻找并处理入度为0的节点，移除其出边，若邻接节点入度变为0则加入处理队列，直到所有节点处理完毕或者发现环

算法核心步骤拆解

1. 初始化 ：遍历所有节点，将入度为0的节点加入队列，作为拓扑排序的起始点，无任何依赖
2. 处理队列 ：取出队首入度为0的节点，加入拓扑排序
3. 更新邻接节点 ：遍历该节点所有出边，对所有邻接节点入度减一，即移除依赖边
4. 重新判断入度：若邻接节点入度变为0，则说明所有前驱依赖已经处理完毕，则加入队列等待处理
5. 环的判断 ：若最终处理完毕的节点数小于总节点数n 则说明图中存在环（环中不存在入度为0的节点 无法加入队列），即无拓扑序，否则队列的处理顺序就是合法拓扑序

三、代码讲解

1. 图存储方式（邻接表）

拓扑排序处理有向图 ，因此邻接表添加单向边 a->b即可，且加边时更新终点入度

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx++; // 邻接表头插法，添加a→b的有向边
}

• 与无向图的区别：无向图即双向图，再添加b->a的边即可，拓扑序中仅存储单向信息
• 入度更新：主函数中add(a,b)后执行in[b]++，更新b点的入度

2.拓扑排序函数topsort()(kahn算法实现)

bool topsort()
{
    int hh = 0,tt = -1;
    // 步骤1：初始化队列，将所有入度为0的节点入队（拓扑排序起始点）
    for(int i = 1;i<=n;i++) if(!in[i]) q[++tt] = i;
    
    // 步骤2：队列非空时，循环处理入度为0的节点
    while(hh<=tt)
    {
        int t = q[hh++]; // 取出队首节点t（处理当前入度为0的节点）
        // 步骤3：遍历t的所有出边，移除出边并更新邻接节点入度
        for(int i = h[t];~i;i = ne[i])  // ~i 等效 i!=-1，遍历t的所有出边
        {
            int j = e[i]; // j是t的邻接节点（t→j）
            // 步骤4：j的入度减1（解除t对j的依赖），若入度为0则入队
            if(--in[j] == 0) q[++tt] = j;
        }
    }
    // 关键：判断是否处理完所有节点（无环）
    // tt初始为-1，入队n个节点则tt = n-1，说明所有节点都入队（存在拓扑序）
    return tt == n-1;
}

核心要点

• 队列初始化 ： for(int i = 1;i<=n;i++) if(!in[i]) q[++tt] = i;
  找到入度为0的所有节点并全部入队才符合贪心策略，且拓扑序不唯一
• 出边遍历及入度更新 ：·--in[j] == 0
  先对j入度减1 ，表示移除t->j的依赖边，若减后为0，则说明j的前驱依赖处理完毕，可以入队
• 环的判断逻辑 ：return tt == n-1
  队列指针tt初始为-1，每入队一个节点tt++，若最终tt == n-1，则恰好n个节点入队并处理，则无环，否则存在环
• 拓扑序列的存储 ：数组q[]为拓扑序列
  由于利用数组模拟队列的特性，节点入队顺序 就是kahn算法处理顺序 ，因此q[0~n-1]就是拓扑排序

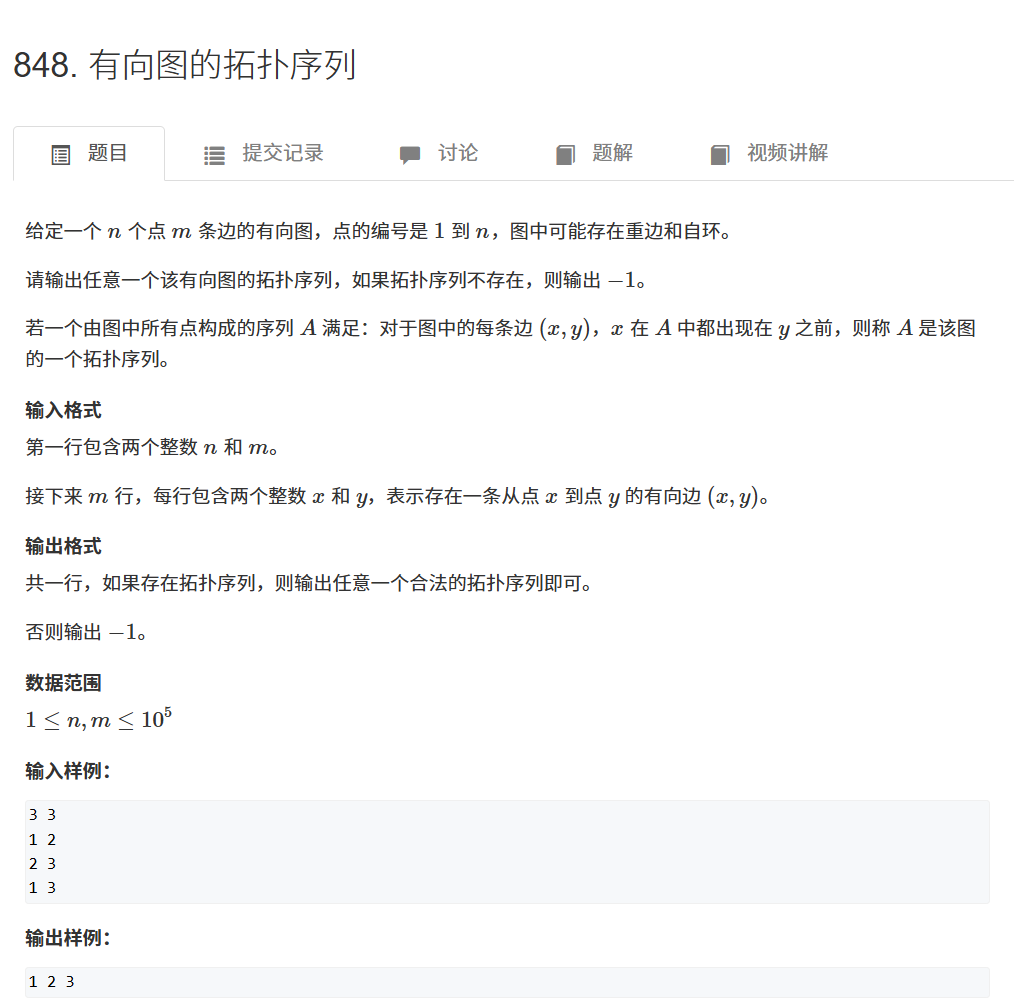
四、题目链接

https://www.acwing.com/problem/content/850/

题解

//topsort拓扑排序  拓扑图：有向无环图，入度：一个点的进边数量，出度：一个点的出边数量
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;
const int N = 1e5+10;

int idx,h[N],e[N],ne[N],in[N],q[N];
int n,m;

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

bool topsort()
{
    int hh = 0,tt = -1;
    for(int i = 1;i<=n;i++) if(!in[i]) q[++tt] = i;  //找到入度为0的点  即为起点 入队
    while(hh<=tt)
    {
        int t = q[hh++];
        for(int i = h[t];~i;i = ne[i])  //遍历该点所有出边
        {
            int j = e[i];
            if(--in[j] == 0) q[++tt] = j;  //每次出队则减少当前点的入度 若入度为0则为新的起点再入队
        }
    }
    return tt == n-1;  //tt起点为-1  若最终为n-1则刚好覆盖所有节点，即存在拓扑排序（能够进入队列的都满足拓扑排序要求，tt移动了n则说明全部满足）
}

int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d",&n,&m);
    while(m--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        in[b]++;  //a->b则b的入度++
    }
    if(!topsort()) puts("-1");
    else
    {
        for(int i = 0;i<n;i++) printf("%d ",q[i]);  //数组模拟队列的特性，队列中前n个为拓扑排序后的结果
    }
    return 0;
}

寒假效率好低~