【递归算法】二叉树剪枝

题目链接：二叉树剪枝

一、题目解析

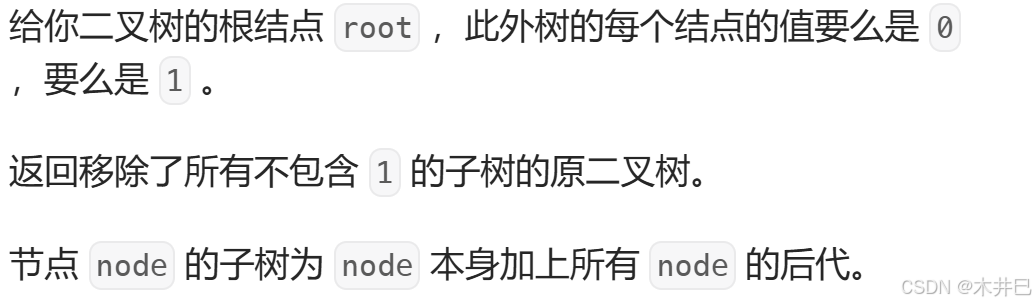
题目要求删除原二叉树中，不包含1的子树，即子节点全为0的子树 ：

---

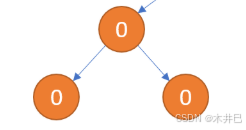
示例2中非常明确的表示了需要被删除的子树的两种情况：

1. 左右子节点均为0且本身也为0
2. 为叶节点
   

---

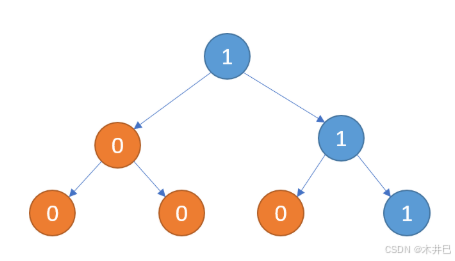
因此，对于每一个节点，我们都需要知道其左右子节点的情况，再结合自身的val，才可以判断是否将该子树删除。

二、算法原理

对于二叉树，自然可以使用递归来解决。

根据题目解析后得到的大致思路，我们需要：

• 先知道某个节点的左右子节点的情况，
• 再结合自身的val

才能判断是否删除以该节点为根的子树。

整个思路其实就是二叉树的后序遍历：

• 先检查左节点
• 再检查右节点
• 最后查看自身的val

---

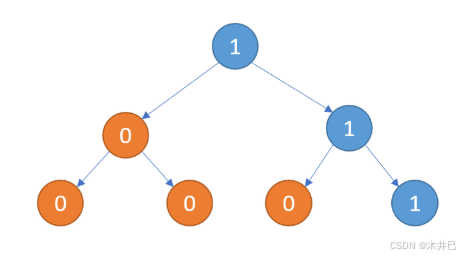
不妨后序遍历二叉树模拟一下整个过程：

• 从根节点1开始，先判断其左子节点
• 走到第一层根节点1的左子节点0处，对于该节点也需要先判断其左子节点
• 走到第二层节点0的左子节点0处，对于该节点也需要先判断其左子节点
• 走到第三层节点0的左子节点null处，由于空节点无法操作，此时返回上一层
• 返回到第三层节点0处，接着判断其右子节点
• 走到第三层节点0的右子节点null处，同样该节点为空，返回上一层
• 返回到第三层节点0处，然后判断其val，发现为0，此时该节点满足了"左右子节点均为空且val为0"的条件，故将该节点删除，返回null
• 返回到第二层节点0处，接着判断其右节点
• 走到第二层节点0的右子节点0处，对于该节点也需要判断其左右子节点，这里省略，该节点被删除，返回null
• 返回的第二层节点0处，然后判断其val，发现为0，此时该节点满足条件，故删除该节点，返回null
• 返回到第一层根节点1处，接着判断其右子节点
• 走到第一层根节点1的右子节点1处，对于该节点也需要判断其左子节点
• 走到第二层节点1的左子节点0处，对于该节点也需要判断其左右子节点，该节点满足删除条件，故删除该节点，返回null
• 返回到第二层节点1处，接着判断其右子节点
• 走到第二层节点1的右子节点处，对于该节点也需要判断其左右子节点，该节点的左右子节点均为空，但是其val不为0，故不将该节点删除，返回该节点地址
• 返回到第二层节点1处，此时其左子节点为空（已被删除）但右子节点不为空，且其val不为0，故不将该节点删除，返回该节点地址
• 返回到第一层根节点1处，此时其左子节点为空（已被删除）但右子节点不为空，且其val不为0，故不将该节点删除，返回该节点地址
• 遍历完成

三、代码实现

根据算法原理，我们设计函数头只需要一个参数------根节点地址，即可。

函数体只需要按照后序遍历来设计就可以了。

递归出口是当遇到空节点时，返回null。

代码如下：

class Solution {
    public TreeNode pruneTree(TreeNode root) {
        // 递归出口
        if (root == null) return null;

		// 递归（后序）
		root.left = pruneTree(root.left);
		root.right = pruneTree(root.right);
	
		// 返回
		if (root.left == null && root.right == null && root.val == 0)
		    root = null;
		return root;
    }
}

---

完