【笔记】《深度学习》-DeepLearning【第一部分】

网站：深度学习

主要参考经典书目《深度学习》，其中有三个部分，因此分为三篇博客，笔记做了很多简化，想要深入学习建议下载原书阅读。

目录

第一章：引言

第一部分：应用数学与机器学习基础

第二章：线性代数

范数

特殊类型的矩阵和向量

特征分解

实例：主成成分分析

第三章：概率与信息论

概率

常用概率分布

信息论

第四章：数值计算

基于梯度的优化方法

[Jacobian 和 Hessian 矩阵](#Jacobian 和 Hessian 矩阵)

实例：线性最小二乘

第五章：机器学习基础

常见任务

促使深度学习发展的挑战

---

第一章：引言

本书讨论一种解决方案，可以让计算机从经验中学习，并根据层次化的概念体系来理解世界，而每个概念则通过与某些相对简单的概念之间的关系来定义。让计算机从经验获取知识，可以避免由人类来给计算机形式化地指定它需要的所有知识。层次化的概念让计算机构建较简单的概念来学习复杂概念。如果绘制出这些概念如何建立在彼此之上的图，我们将得到一张"深"(层次很多)的图。基于这个原因，我们称这种方法为AI深度学习(deeplearning)。

深度学习模型示意图：

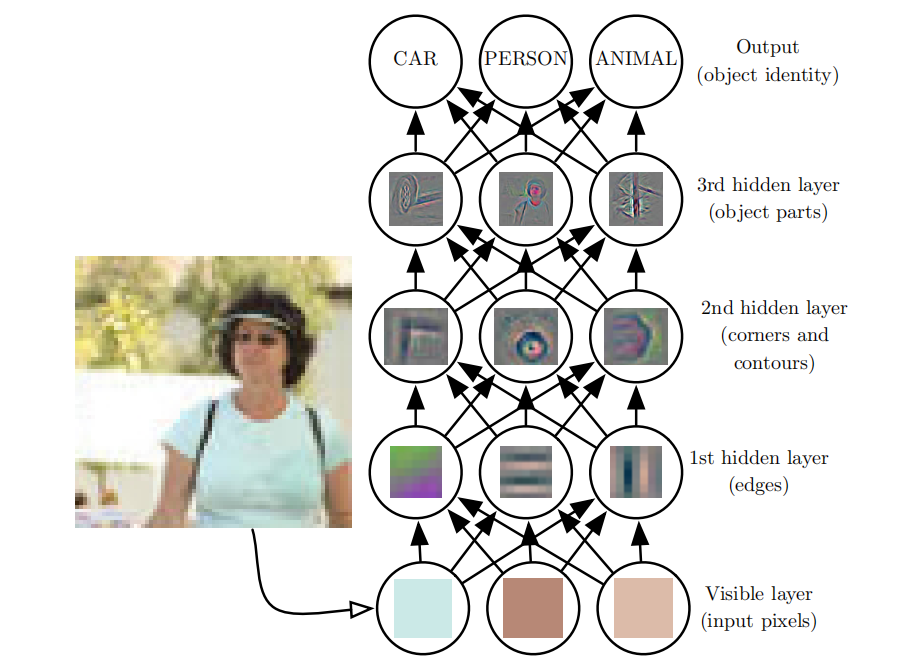
这本书对各类读者都有一定用处，但我们主要是为两类受众对象而写的。其中一类受众对象是学习机器学习的大学生(本科或研究生) ，包括那些已经开始职业生涯的深度学习和人工智能研究者。另一类受众对象是没有机器学习或统计背景但希望能快速地掌握这方面知识并在他们的产品或平台中使用深度学习的软件工程师 。深度学习在许多软件领域都已被证明是有用的，包括计算机视觉、语音和音频处理、自然语言处理、机器人技术、生物信息学和化学、电子游戏、搜索引擎、网络广告和金融。

为了最好地服务各类读者，我们将本书组织为三个部分。第一部分介绍基本的数学工具和机器学习的概念。第二部分介绍最成熟的深度学习算法，这些技术基本上已经得到解决。第三部分讨论某些具有展望性的想法，它们被广泛地认为是深度学习未来的研究重点。

读者可以随意跳过不感兴趣或与自己背景不相关的部分。熟悉线性代数、概率和基本机器学习概念的读者可以跳过第一部分，例如，当读者只是想实现一个能工作的系统则不需要阅读超出第二部分的内容。为了帮助读者选择章节，图1.6展示了这本书的高层组织结构的流程图。

我们假设所有读者都具备计算机科学背景。也假设读者熟悉编程，并且对计算的性能问题、复杂性理论、人门级微积分和一些图论术语有基本的了解。

第一部分：应用数学与机器学习基础

本书这一部分将介绍理解深度学习所需的基本数学概念。我们从应用数学的一般概念开始，这能使我们定义许多变量的函数，找到这些函数的最高和最低点，并量化信念度。接着，我们描述机器学习的基本目标，并描述如何实现这些目标。我们需要指定代表某些信念的模型、设计衡量这些信念与现实对应程度的代价函数以及使用训练算法最小化这个代价函数。
这个基本框架是广泛多样的机器学习算法的基础，其中也包括非深度的机器学习方法。在本书的后续部分，我们将在这个框架下开发深度学习算法。

第二章：线性代数

先来认识标量，向量，矩阵和张量

• 标量（scalar） ：一个标量就是一个单独的数。
• 向量（vector） ：一个向量是一列数。这些数是有序排列的。通过次序中的索引，我们可以确定每个单独的数。
• 矩阵（matrix） ：矩阵是一个二维数组，其中的每一个元素被两个索引（而非一个）所确定。
• 张量（tensor） ：在某些情况下，我们会讨论坐标超过两维的数组。一般地，一个数组中的元素分布在若干维坐标的规则网格中，我们称之为张量。

|----------------------------------------------------------------------------|----------------------------------------------------------------------------|
| 向量 | 矩阵 |
| | |

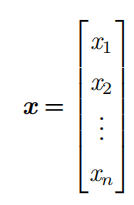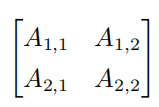转置（transpose ）： 是矩阵的重要操作之一。矩阵的转置是以对角线为轴的镜像，这条从左上角到右下角的对角线被称为主对角线 （main diagonal ）。

矩阵和向量相加，产生另一个矩阵：C = A + b ，其中 C i,j = A i,j + b j 。换言之，向量 b 和矩阵
A 的每一行相加。这个简写方法使我们无需在加法操作前定义一个将向量 b 复制到每一行而生成的矩阵。这种隐式地复制向量 b 到很多位置的方式，被称为 广播（broadcasting） 。

矩阵乘法

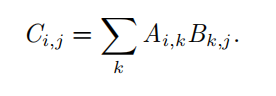
需要注意的是，两个矩阵的标准乘积 不是 指两个矩阵中对应元素的乘积。不过，那样的矩阵操作确实是存在的，被称为 元素对应乘积 （element-wise product ） 或者 Hadamard 乘积 （ Hadamard product ），记为 A ⊙ B 。
单位矩阵（identity matrix ）

矩阵 A 的 矩阵逆（matrix inversion **）**记作 A − 1

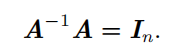
线性组合（linear combination ）
形式上，一组向量的线性组合，是指每个向量乘以对应标量系数之后的和，即：

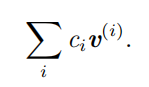
生成子空间（span **）**是原始向量线性组合后所能抵达的点的集合。
线性无关（linearly independent **）：**一组向量中的任意一个向量都不能表示成其他向量的线性组合，那么这组向量称为线性无关
一个列向量线性相关的方阵被称为 奇异的（singular）

范数

有时我们需要衡量一个向量的大小。在机器学习中，我们经常使用被称为 范数（norm **）**的函数衡量向量大小。形式上， L p 范数定义如下

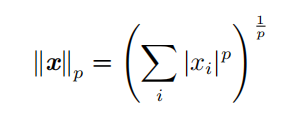
范数（包括 L p 范数）是将向量映射到非负值的函数。直观上来说，向量 x 的范数衡量从原点到点 x 的距离。更严格地说，范数是满足下列性质的任意函数：

一些常用范数：

|-------------------------------------|--------------------------------------------------------------------------------------------------------------------------------------------------|
| L 2 范数 | 被称为 欧几里得范数（Euclidean norm ） 。它表示从原点出发到向量 x 确定的点的欧几里得距离 简单地通过点积 x ⊤ x 计算 常简化表示为 ∥ x ∥ ，略去了下标 2 |
| L 1 范数 | |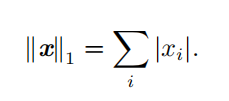
| L 0 范数 | 有时候我们会统计向量中非零元素的个数来衡量向量的大小。有些作者将这种函数称为 " L 0 范数 '' ，但是这个术语在数学意义上是不对的。向量的非零元素的数目不是范数，因为对向量缩放 α 倍不会改变该向量非零元素的数目。因此， L 1 范数经常作为表示非零元素数目的替代函数。 |
| L ∞ 范数 | 也被称为 最大范数这个范数表示向量中具有最大幅值的元素的绝对值： |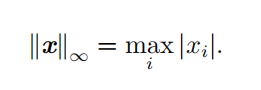
| Frobenius 范数 （ Frobenius norm ） | 衡量矩阵的大小 |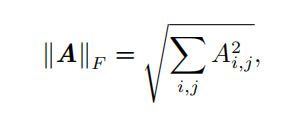

特殊类型的矩阵和向量

对角矩阵（diagonal matrix **）**只在主对角线上含有非零元素，其他位置都是零。
对称（symmetric ）矩阵是转置和自己相等的矩阵：

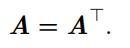
单位向量（unit vector **）**是具有 单位范数 （ unit norm ）的向量：

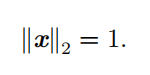
正交矩阵（orthogonal matrix **）**是指行向量和列向量是分别标准正交的方阵：

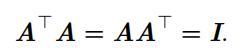
向量不仅互相正交，并且范数都为 1 ，那么我们称它们是 标准正交 （orthonormal）。

特征分解

特征分解（eigendecomposition ） 是使用最广的矩阵分解之一，即我们将矩阵分解成一组特征向量（v）和特征值（）。

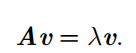
A 的 特征分解 （ eigendecomposition ）可以记作

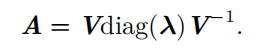
前提是A有n个线性无关的特征向量。
所有特征值都是正数的矩阵被称为 正定（positive definite ） ；所有特征值都是非负数的矩阵被称为半正定 （positive semidefinite ） 。同样地，所有特征值都是负数的矩阵被称为负定（negative definite ）；所有特征值都是非正数的矩阵被称为 半负定 （negative semidefinite）。
奇异值分解
还有另一种分解矩阵的方法，被称为奇异值分解（ singular value decomposition, SVD ），将矩阵分解为 奇异向量 （ singular vector ）和 奇异值 （ singular value ）。
然而，奇异值分解有更广泛的应用。每个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这时我们只能使用奇异值分解。

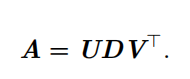
这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵 U 和 V 都定义为正交矩阵，而矩阵 D 定义为对角矩阵。注意，矩阵 D 不一定是方阵。
对角矩阵 D 对角线上的元素被称为矩阵 A 的 奇异值 （ singular value ）。矩阵 U 的列向量被称为 左奇异向量 （ left singular vector ），矩阵 V 的列向量被称 右奇异向量（ right singular vector ）。
事实上，我们可以用与 A 相关的特征分解去解释 A 的奇异值分解。 A 的 左奇异向量（ left singular vector ）是 AA ⊤ 的特征向量。 A 的 右奇异向量 （ right singular vector）是 A ⊤ A 的特征向量。 A 的非零奇异值是 A ⊤ A 特征值的平方根，同时也是 AA ⊤ 特征值的平方根。

Moore-Penrose 伪逆
矩阵 A的伪逆定义为：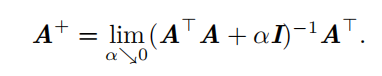

实际计算采用：

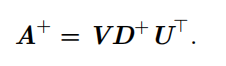
对角矩阵 D 的伪逆 D + 是其非零元素取倒数之后再转置得到的。

迹运算返回的是矩阵对角元素的和：

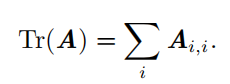
行列式，记作 det(A) ，是一个将方阵 A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。如果行列式是 0 ，那么空间至少沿着某一维完全收缩了，使其失去了所有的体积。如果行列式是 1 ，那么这个转换保持空间体积不变。

实例：主成成分分析

主成分分析（principal components analysis, PCA **）**是一个简单的机器学习算法，可以通过基础的线性代数知识推导。

PCA 的核心： 找到数据中方差最大的若干个 "方向"（主成分），将高维数据投影到这些方向上，用少数几个主成分（2-3 个）替代原始高维特征，同时保留数据的核心信息（方差）。

给出python示例

# 导入核心库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs  # 生成模拟IMU类数据

# ---------------------- 步骤1：生成模拟高维数据（模拟IMU/EMG数据） ----------------------
# 生成3类高维数据（模拟3种动作的IMU数据：走路、跑步、静坐）
# 原始维度：10维（模拟IMU的6轴信号+4个统计特征），样本数：300个
X, y = make_blobs(
    n_samples=300,  # 300个样本
    n_features=10,  # 10维特征（高维）
    centers=3,      # 3类数据（3种动作）
    cluster_std=[1.0, 1.2, 0.8],  # 每类数据的方差
    random_state=42  # 固定随机种子，结果可复现
)

# 转换为DataFrame，方便后续处理（可选）
feature_names = [f"IMU_feature_{i+1}" for i in range(10)]
df = pd.DataFrame(X, columns=feature_names)
df["label"] = y  # 标签：0=走路，1=跑步，2=静坐

# ---------------------- 步骤2：数据标准化（PCA必须步骤） ----------------------
# 提取特征列（去掉标签）
X_features = df[feature_names].values
# 标准化：均值=0，方差=1
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_features)

# ---------------------- 步骤3：PCA降维 ----------------------
# 1. 先拟合PCA，查看所有主成分的方差解释率
pca = PCA()
X_pca_all = pca.fit_transform(X_scaled)

# 计算方差解释率和累计方差解释率
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)

# 打印方差解释率（直观看前几个主成分能保留多少信息）
print("各主成分的方差解释率：")
for i, ratio in enumerate(explained_variance_ratio[:5]):  # 打印前5个
    print(f"PC{i+1}: {ratio:.4f} ({ratio*100:.2f}%)")

print("\n累计方差解释率：")
for i, cum_ratio in enumerate(cumulative_variance_ratio[:5]):
    print(f"前{i+1}个主成分: {cum_ratio:.4f} ({cum_ratio*100:.2f}%)")

# 2. 选择前2个主成分（累计方差解释率≥85%，适合可视化）
pca_2d = PCA(n_components=2)  # 降维到2维
X_pca_2d = pca_2d.fit_transform(X_scaled)

# ---------------------- 步骤4：可视化 ----------------------
plt.rcParams["font.sans-serif"] = ["SimHei"]  # 解决中文显示
plt.rcParams["axes.unicode_minus"] = False    # 解决负号显示

# 子图1：方差解释率条形图（看每个主成分的贡献）
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# 子图1：方差解释率
ax1.bar(
    x=[f"PC{i+1}" for i in range(10)],
    height=explained_variance_ratio,
    color="#1f77b4",
    alpha=0.7
)
ax1.plot(
    [f"PC{i+1}" for i in range(10)],
    cumulative_variance_ratio,
    color="red",
    marker="o",
    label="累计方差解释率"
)
ax1.axhline(y=0.85, color="orange", linestyle="--", label="85%阈值")
ax1.set_xlabel("主成分")
ax1.set_ylabel("方差解释率")
ax1.set_title("PCA方差解释率（前10个主成分）")
ax1.legend()
ax1.grid(axis="y", alpha=0.3)

# 子图2：PCA降维后2D可视化（区分3类数据）
colors = ["#1f77b4", "#ff7f0e", "#2ca02c"]  # 3类数据的颜色
labels = ["走路", "跑步", "静坐"]
for i in range(3):
    mask = (y == i)
    ax2.scatter(
        X_pca_2d[mask, 0],  # PC1
        X_pca_2d[mask, 1],  # PC2
        c=colors[i],
        label=labels[i],
        alpha=0.7,
        s=50  # 点的大小
    )
ax2.set_xlabel(f"第一主成分（PC1，解释率：{pca_2d.explained_variance_ratio_[0]:.4f}）")
ax2.set_ylabel(f"第二主成分（PC2，解释率：{pca_2d.explained_variance_ratio_[1]:.4f}）")
ax2.set_title("PCA降维后2D可视化（IMU数据3类动作）")
ax2.legend()
ax2.grid(alpha=0.3)

plt.tight_layout()
plt.show()

# ---------------------- 可选：降维到3D并可视化 ----------------------
from mpl_toolkits.mplot3d import Axes3D

# PCA降维到3维
pca_3d = PCA(n_components=3)
X_pca_3d = pca_3d.fit_transform(X_scaled)

# 3D可视化
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection="3d")
for i in range(3):
    mask = (y == i)
    ax.scatter(
        X_pca_3d[mask, 0],
        X_pca_3d[mask, 1],
        X_pca_3d[mask, 2],
        c=colors[i],
        label=labels[i],
        alpha=0.7,
        s=50
    )
ax.set_xlabel(f"PC1（{pca_3d.explained_variance_ratio_[0]:.4f}）")
ax.set_ylabel(f"PC2（{pca_3d.explained_variance_ratio_[1]:.4f}）")
ax.set_zlabel(f"PC3（{pca_3d.explained_variance_ratio_[2]:.4f}）")
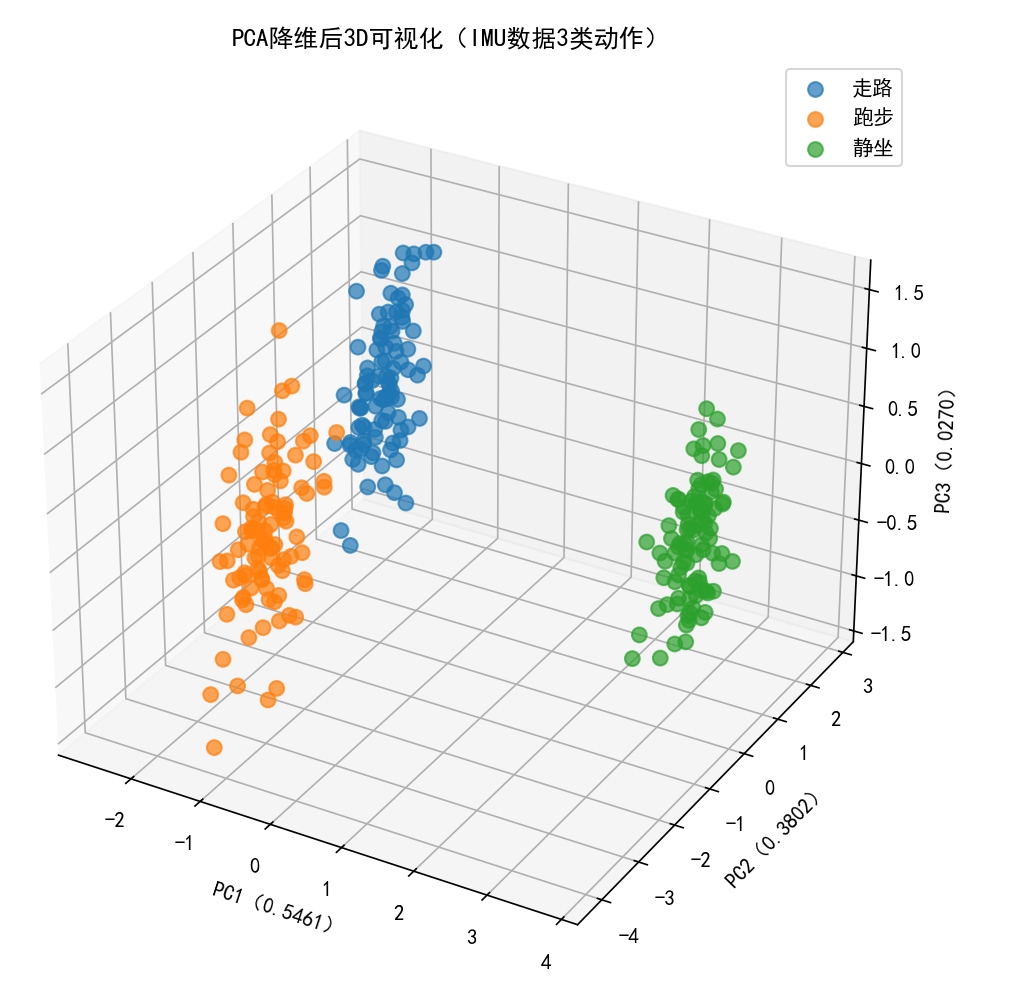
ax.set_title("PCA降维后3D可视化（IMU数据3类动作）")
ax.legend()
plt.show()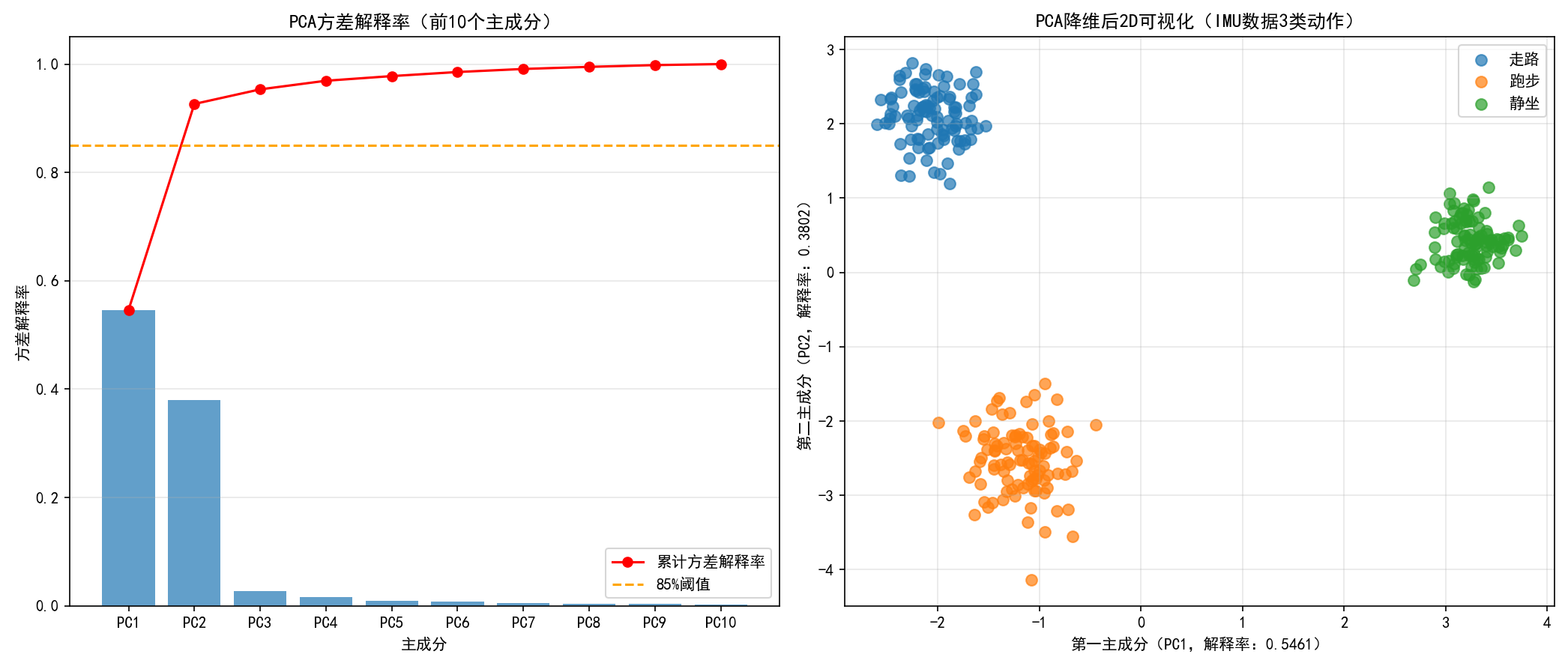

第三章：概率与信息论

概率论使我们能够提出不确定的声明以及在不确定性存在的情况下进行推理，而信息论使我们能够量化概率分布中的不确定性总量。

概率

用概率来表示一种 信任度 （degree of belief）。 概率，直接与事件发生的频率相联系，被称为 频率派概率（frequentist probability ） ；涉及到确定性水平，被称为 贝叶斯概率 （Bayesian probability）。
随机变量（random variable **）**是可以随机地取不同值的变量
概率分布（probability distribution **）**用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小。我们描述概率分布的方式取决于随机变量是离散的还是连续的。

|-------|---------------------------------------------------------------------------------------------------------------------------------|
| 离散型变量 | 概率质量函数（probability mass function, PMF） 概率质量函数可以同时作用于多个随机变量。这种多个变量的概率分布被称 为 联合概率分布（joint probability distribution ）。 |
| 连续型变量 | 用 概率密度函数（probability density function, PDF） |

几种概率

|----------|-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 边缘概率 | 有时候，我们知道了一组变量的联合概率分布，但想要了解其中一个子集的概 率分布。这种定义在子集上的概率分布被称为 边缘概率分布 （ marginal probability distribution ）。 求和法则（sum rule **）**来计算 P ( x ) ： |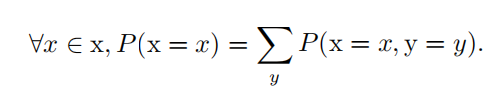
| 条件概率 | 我们将给定 x = x ， y = y 发生的条件概率记为 P ( y = y | x = x ) 。 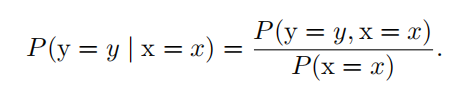任何多维随机变量的联合概率分布，都可以分解成只有一个变量的条件概率相 乘的形式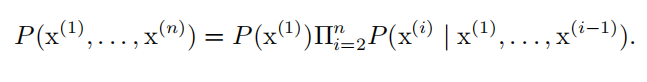： 这个规则被称为概率的 链式法则（chain rule **）**或者 乘法法则（product rule ）。 |

独立性和条件独立性
两个随机变量 x 和 y ，如果它们的概率分布可以表示成两个因子的乘积形式，并且一个因子只包含 x 另一个因子只包含 y ，我们就称这两个随机变量是 相互独立的（independent ）：

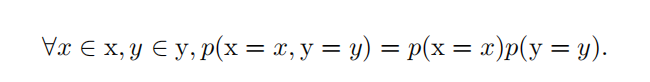
期望，方差和协方差

|---------------------|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 期望（expectation） | 对于离散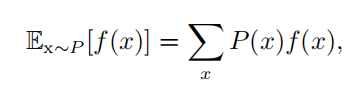型 对于连续型 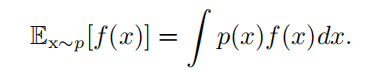期望是线性的 |
| 方差（variance） | |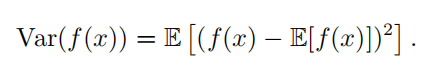
| 协方差（covariance） | 在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度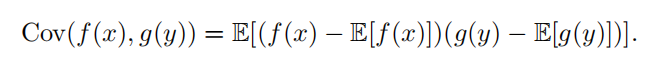： 协方差矩阵 （ covariance matrix 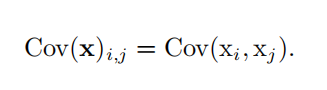） 对角元素是方差 |

常用概率分布

|-------------------------------------------------------------------------------------|-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| Bernoulli 分布 （ Bernoulli distribution ） | 具有如下性质： |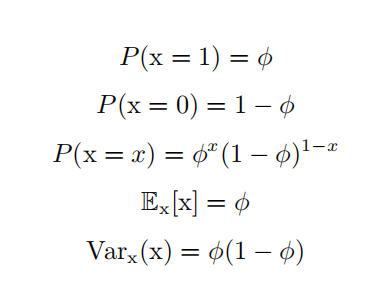
| Multinoulli 分布 （ multinoulli distribution ） 或者 范畴分布 （ categorical distribution） | |
| 正态分布 （ normal distribution ） 也称为 高斯分布 （ Gaussian distribution 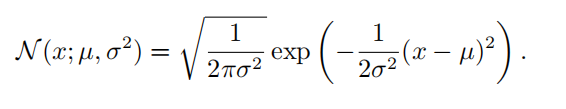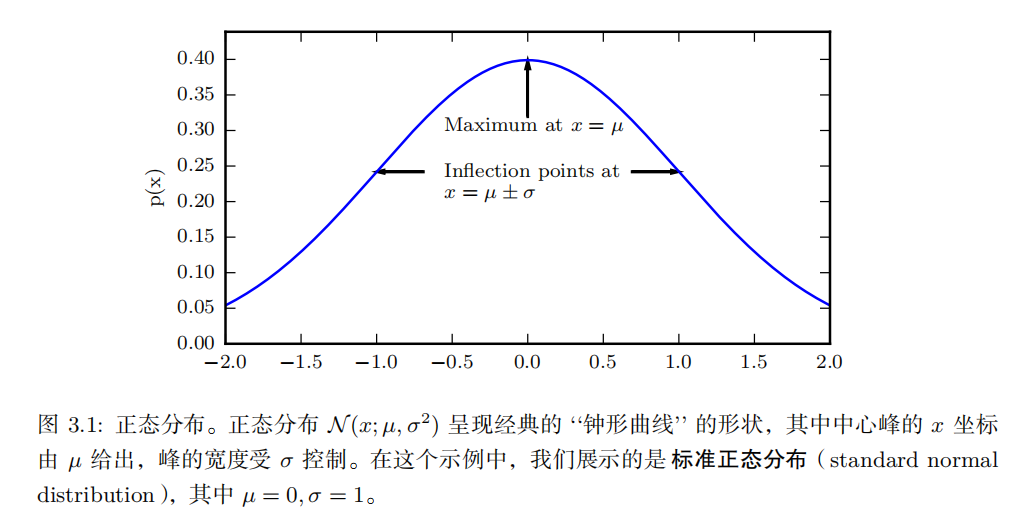）： | 多维正态分布 （ multivariate normal distribution）。它的参数是一个正定对称矩阵 Σ ： |
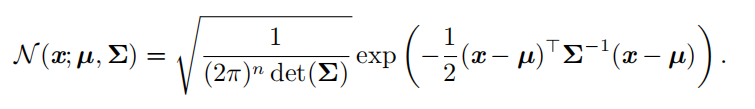| 指数分布 （ exponential distribution ） | |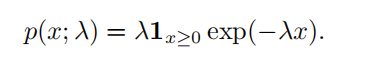
| Laplace 分布 （ Laplace distribution ） | |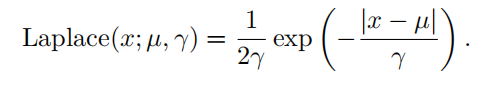
| Dirac 分布 | 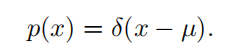Dirac 分布经常作为 经验分布 （ empirical distribution ）的一个组成部分出现 |
| 经验分布 （empirical distribution） | |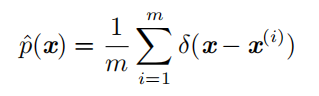
| 混合分布 （ mixture distribution ） | 混合分布由一些组件 (component) 分布构成。每次实验，样本是由哪个组件分布产生的取决于从一个 Multinoulli 分布中采样的结果： |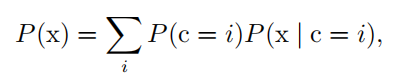

贝叶斯规则
我们经常会需要在已知 P ( y | x ) 时计算 P ( x | y ) 。幸运的是，如果还知道 P ( x ) ，我们可以用 贝叶斯规则 （ Bayes' rule ）来实现这一目的：

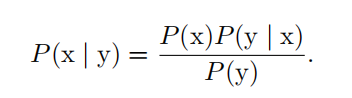
连续型随机变量和概率密度函数的深入理解需要用到数学分支 测度论 （ measure theory）的相关内容来扩展概率论

信息论

信息论是应用数学的一个分支，主要研究的是对一个信号包含信息的多少进行量化信息论的基本想法是一个不太可能的事件居然发生了，要比一个非常可能的事件发生，能提供更多的信息。

三个性质：

• 非常可能发生的事件信息量要比较少，并且极端情况下，确保能够发生的事件应该没有信息量。
• 较不可能发生的事件具有更高的信息量。
• 独立事件应具有增量的信息。例如，投掷的硬币两次正面朝上传递的信息量，应该是投掷一次硬币正面朝上的信息量的两倍。

我们定义一个事件 x = x 的 自信息 （ self-information ）

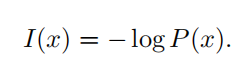
• I(x) 单位：奈特**（nats** ）。一奈特是以 1 e的概率观测到一个事件时获得的信息量。
• 其他的材料中使用底数为 2 的对数，单位是 比特（bit **）**或者 香农（shannons ）
• 通过比特度量的信息只是通过奈特度量信息的常数倍。

自信息只处理单个的输出。我们可以用 香农熵 （ Shannon entropy ）来对整个概率分布中的不确定性总量进行量化：

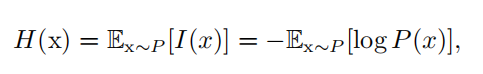
如果我们对于同一个随机变量 x 有两个单独的概率分布 P ( x ) 和 Q ( x ) ，我们可以使用 KL 散度 （ Kullback-Leibler (KL) divergence ）来衡量这两个分布的差异：

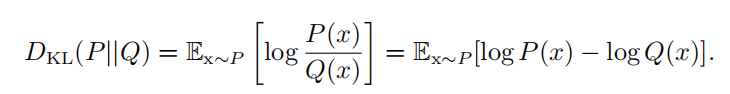
一个和 KL 散度密切联系的量是 交叉熵 （ cross-entropy ） H ( P, Q ) = H ( P ) + D KL ( P || Q ) ，它和 KL 散度很像但是缺少左边一项：

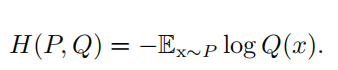
第四章：数值计算

下溢 （ underflow ）：是一种舍入误差，当接近零的数被四舍五入为零时发生下溢。
上溢 （ overflow ）：当大量级的数被近似为 ∞ 或 −∞ 时发生上溢。

病态条件
条件数表征函数相对于输入的微小变化而变化的快慢程度。输入被轻微扰动而迅速改变的函数对于科学计算来说可能是有问题的，因为输入中的舍入误差可能导致输出的巨大变化。
考虑函数 f ( x ) = A − 1 x 。当 A ∈ R n × n 具有特征值分解时，其条件数为

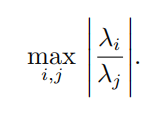
基于梯度的优化方法

我们把要最小化或最大化的函数称为 目标函数 （ objective function ）或 准则（criterion ）。当我们对其进行最小化时，我们也把它称为 代价函数 （ cost function ）、损失函数（ loss function ）或 误差函数 （ error function ）。
导数 f ′ ( x ) 代表 f ( x ) 在点 x 处的斜率。换句话说，它表明如何缩放输入的小变化才能在输出获得相应的变化：f ( x + ϵ ) ≈ f ( x ) + ϵf ′ ( x ) 。
因此我们可以将 x 往导数的反方向移动一小步来减小 f ( x ) 。这种技术被称为 梯度下降（gradient descent ）

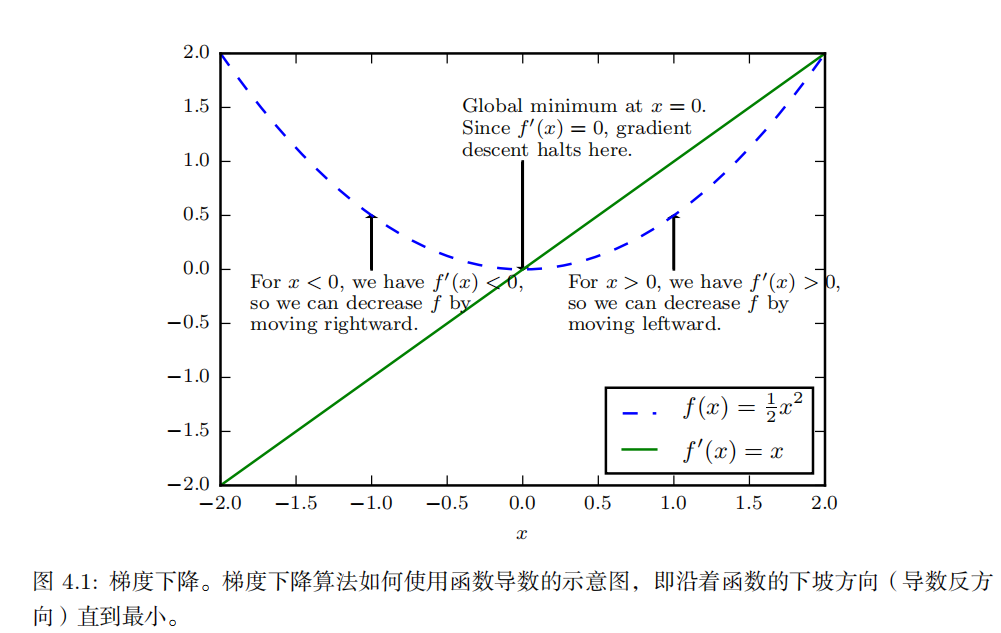
当 f ′ ( x ) = 0 ，导数无法提供往哪个方向移动的信息。 f ′ ( x ) = 0 的点称为 临界点（ critical point ）或 驻点 （ stationary point ）。一个 局部极小点 （ local minimum ）意味着这个点的 f ( x ) 小于所有邻近点，因此不可能通过移动无穷小的步长来减小 f ( x ) 。一个 局部极大点 （ local maximum ）意味着这个点的 f ( x ) 大于所有邻近点，因此不可能通过移动无穷小的步长来增大 f ( x )。有些临界点既不是最小点也不是最大点。这些点被称为 鞍点 （ saddle point ）。

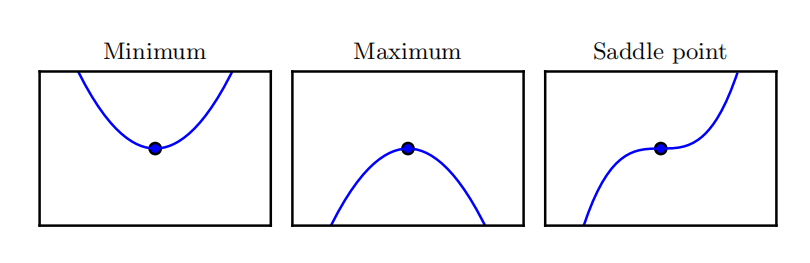
使 f ( x ) 取得绝对的最小值（相对所有其他值）的点是 全局最小点 （ global minimum）。函数可能只有一个全局最小点或存在多个全局最小点，还可能存在不是全局最优的局部极小点。

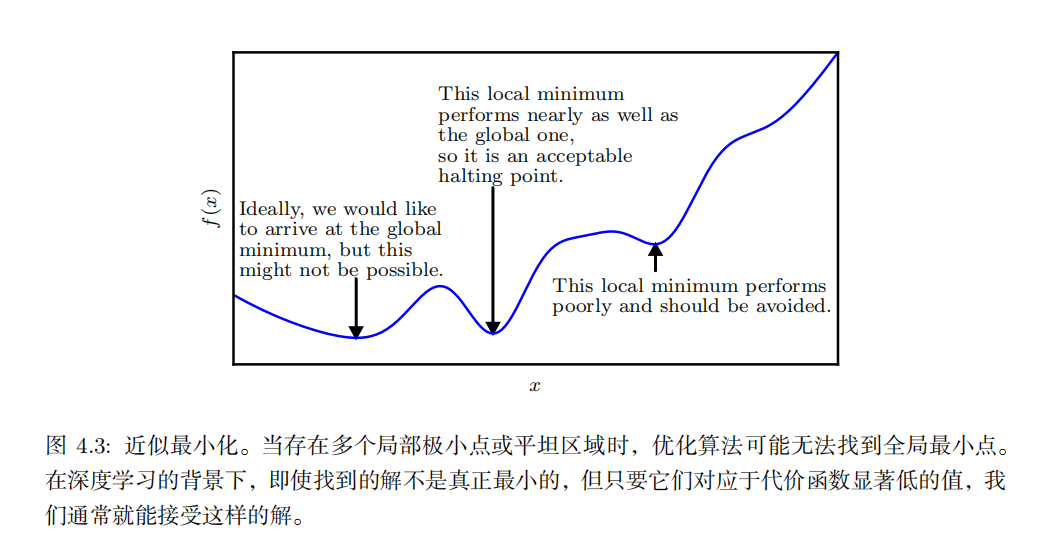
针对具有多维输入的函数，我们需要用到 偏导数 （ partial derivative ）的概念。 梯度 （ gradient ）是相对一个向量求导的导数: f 的导数是包含所有偏导数的向量，记为 ∇ x f ( x ) 。梯度的第 i 个元素是 f 关于 x i 的偏导数。在多维情况下，临界点是梯度中所有元素都为零的点。
为了最小化 f ，我们希望找到使 f 下降得最快的方向。计算方向导数：

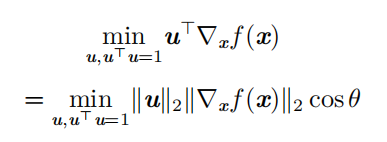
梯度向量指向上坡，负梯度向量指向下坡。我们在负梯度方向上移动可以减小 f 。这被称为 最速下降法 (method of steepest descent) 或 梯度下降 （ gradient descent ）。
最速下降建议新的点为

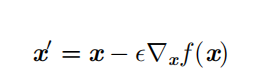
Jacobian和 Hessian矩阵

雅可比矩阵是向量值函数 的一阶偏导数构成的矩阵 ，描述输入向量的微小变化对输出向量的所有维度的变化率 ，是一元函数导数在多元向量值函数上的推广。
当我们的函数具有多维输入时，二阶导数也有很多。我们可以将这些导数合并成一个矩阵，称为 Hessian矩阵。Hessian 矩阵 H ( f )( x ) 定义为

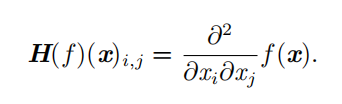
Hessian 等价于梯度的 Jacobian 矩阵
微分算子在任何二阶偏导连续的点处可交换，也就是它们的顺序可以互换：

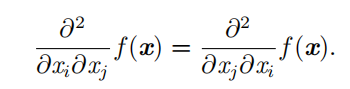
二阶导数 还可以被用于确定一个临界点是否是局部极大点、局部极小点或鞍点，这就是所谓的 二阶导数测试（ second derivative test）。例如，二阶导＜0，是局部极大值点，＞0是局部极小值点。不幸的是，当 f ′′ ( x ) = 0 时测试是不确定的。在这种情况下， x可以是一个鞍点或平坦区域的一部分。

雅可比 ：向量值函数的一阶变化率，m×n矩阵，核心做局部线性近似，是反向传播、EKF 滤波的基础；

海森 ：标量值函数的二阶曲率，n×n对称方阵，核心做二阶泰勒近似，是牛顿法、凸性分析的基础；

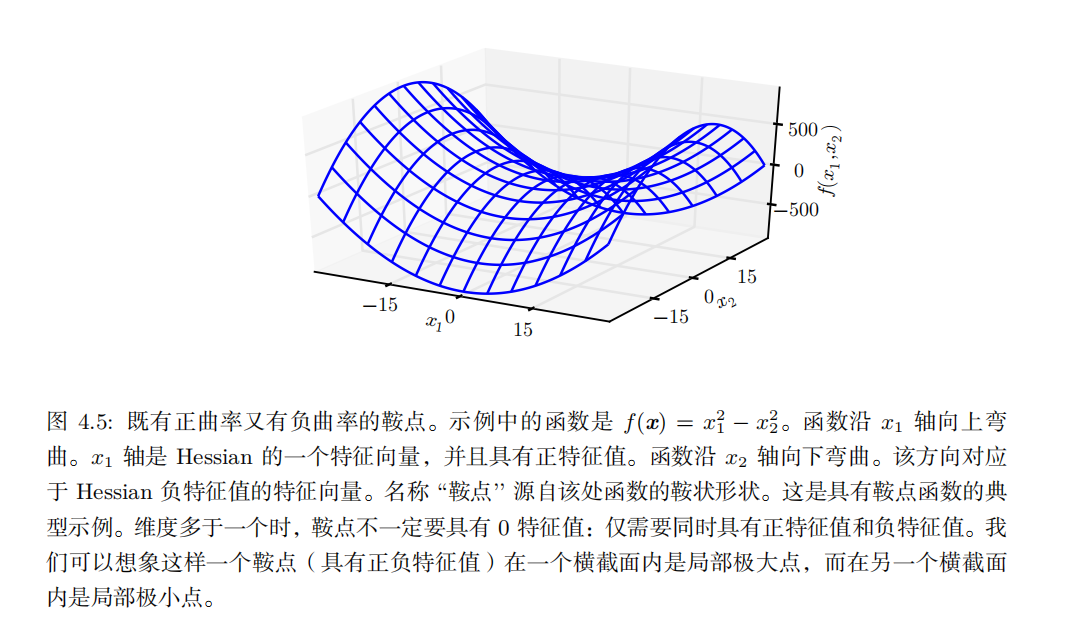
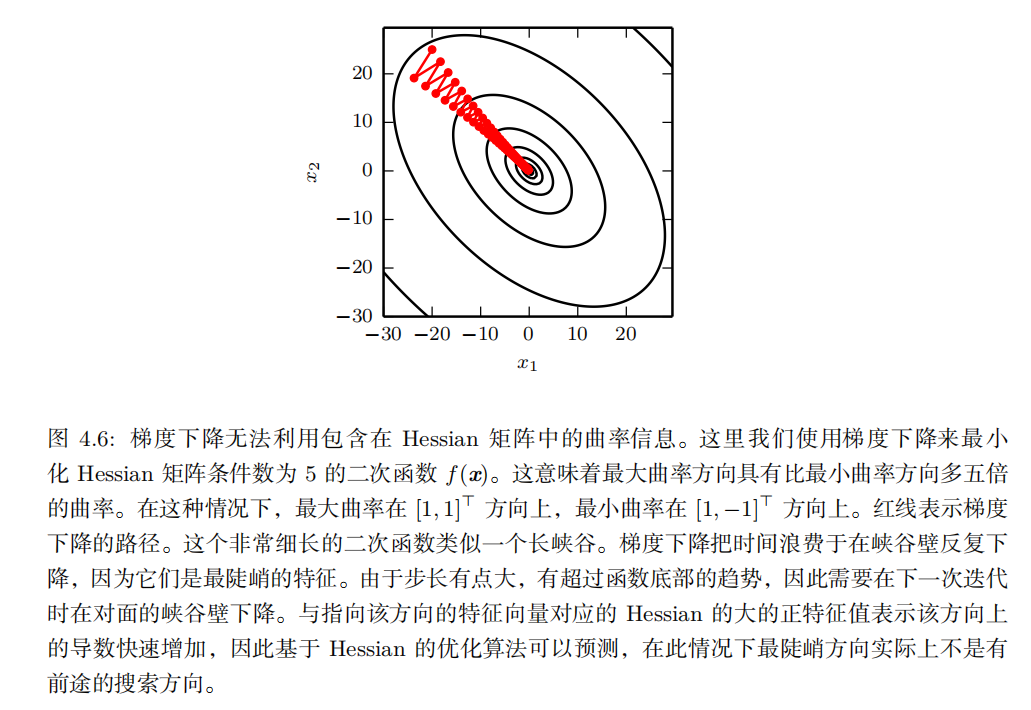
我们可以使用 Hessian 矩阵的信息来指导搜索，以解决这个问题。其中最简单的方法是 牛顿法 （ Newton's method ）。牛顿法基于一个二阶泰勒展开来近似 x (0) 附近的 f ( x ) ：

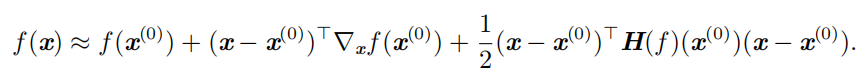
接着通过计算，我们可以得到这个函数的临界点：

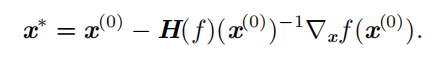
仅使用梯度信息的优化算法被称为 一阶优化算法 (first-order optimization algorithms)，如梯度下降。使用 Hessian 矩阵的优化算法被称为 二阶最优化算法(second-order optimization algorithms)(Nocedal and Wright, 2006)，如牛顿法。

实例：线性最小二乘

将损失函数矩阵化

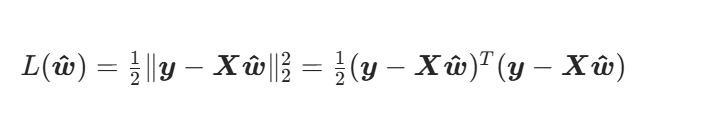
将矩阵形式的损失函数展开

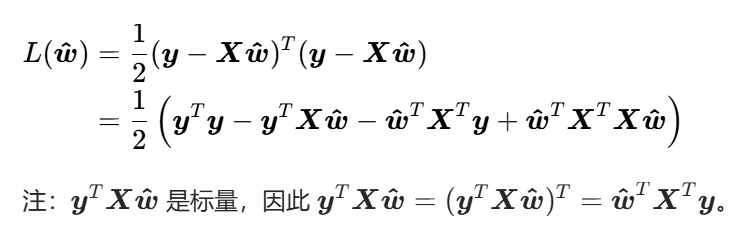
求损失函数的一阶梯度

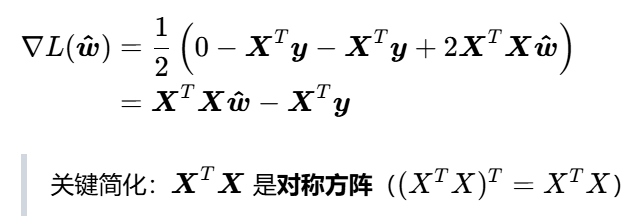
令梯度为0，求极值点

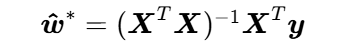
这就是线性最小二乘的闭式解（直接计算，无需迭代优化），也是工程中最常用的求解公式。

计算海森矩阵，证明极值点是全局最小点

第五章：机器学习基础

Mitchell (1997) 提供了一个简洁的定义： '' 对于某类任务 T 和性能度量 P ，一个计算机程序被认为可以从经验 E 中学习是指，通过经验 E 改进后，它在任 务 T 上由性能度量 P 衡量的性能有所提升 "
通常机器学习任务定义为机器学习系统应该如何处理 样本 （ example ）

常见任务

机器学习可以解决很多类型的任务。一些非常常见的机器学习任务列举如下：

|-------------------|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 分类 | 在这类任务中，计算机程序需要指定某些输入属于 k 类中的哪一类。为了完成这个任务，学习算法通常会返回一个函数 f: R n → { 1 , . . . , k } 。当 y = f ( x ) 时，模型将向量 x 所代表的输入分类到数字码 y所代表的类别。 例如，Willow Garage PR2 机器人能像服务员一样识别不同饮料，并送给点餐的顾客 (Goodfellow et al. , 2010) 。目前，最好的对象识别工作正是基于深度学习的 (Krizhevsky et al. , 2012a; Ioffe and Szegedy, 2015)。对象识别同时也是计算机识别人脸的基本技术，可用于标记相片合辑中的人脸 (Taigman et al. , 2014) ，有助于计算机更自然地与用户交互。 |
| 输入缺失分类 | 当输入向量的每个度量不被保证的时候，分类问题将会变得更有挑战性。为了解决分类任务，学习算法只需要定义一个从输入向量映射到输出类别的函数。当一些输入可能丢失时，学习算法必须学习一组 函数，而不是单个分类函数。每个函数对应着分类具有不同缺失输入子集的 x 。 这种情况在医疗诊断中经常出现，因为很多类型的医学测试是昂贵的，对身体有害的。有效地定义这样一个大集合函数的方法是学习所有相关变量的概率分布，然后通过边缘化缺失变量来解决分类任务。使用 n个输入变量，我们现在可以获得每个可能的缺失输入集合所需的所有 2 n 个不同的分类函数，但是计算机程序仅需要学习一个描述联合概率分布的函数。参见 Goodfellow et al. (2013d) 了解以这种方式将深度概率模型应用于这类任务的示例。本节中描述的许多其他任务也可以推广到缺失输入的情况; 缺失输入分类只是机器学习能够解决的问题的一个示例。 |
| 回归 | 在这类任务中，计算机程序需要对给定输入预测数值。为了解决这个任务，学习算法需要输出函数 f: R n → R 。除了返回结果的形式不一样外，这类问题和分类问题是很像的。这类任务的一个示例是预测投保人的索赔金额（用于设置保险费），或者预测证券未来的价格。这类预测也用在算法交易中。 |
| 转录 | 这类任务中，机器学习系统观测一些相对非结构化表示的数据，并转录信息为离散的文本形式。例如，光学字符识别要求计算机程序根据文本图片返回文字序列（ASCII 码或者 Unicode 码）。谷歌街景以这种方式使用深度学习处理街道编号 (Goodfellow et al. , 2014d) 。另一个例子是语音识别，计算机程序输入一段音频波形，输出一序列音频记录中所说的字符或单词 ID 的编码。深度学习是现代语音识别系统的重要组成部分，被各大公司广泛使用，包括微软，IBM 和谷歌 (Hinton et al. , 2012b) 。 |
| 机器翻译 | 在机器翻译任务中，输入是一种语言的符号序列，计算机程序必须将其转化成另一种语言的符号序列。这通常适用于自然语言，如将英语译成法语。最近，深度学习已经开始在这个任务上产生重要影响 (Sutskever et al. ,2014; Bahdanau et al. , 2015) 。 |
| 结构化输出 | 结构化输出任务的输出是向量或者其他包含多个值的数据结构，并且构成输出的这些不同元素间具有重要关系。这是一个很大的范畴，包括上述转录任务和翻译任务在内的很多其他任务。例如语法分析------映射自然语言句子到语法结构树，并标记树的节点为动词、名词、副词等等。参考 Collobert(2011) 将深度学习应用到语法分析的示例。另一个例子是图像的像素级分割，将每一个像素分配到特定类别。例如，深度学习可用于标注航拍照片中的道路位置 (Mnih and Hinton, 2010)。在这些标注型的任务中，输出的结构形式不需要和输入尽可能相似。例如，在为图片添加描述的任务中，计算机程序观察到一幅图，输出描述这幅图的自然语言句子 (Kiros et al. , 2014a,b; Mao et al. ,2014; Vinyals et al. , 2015b; Donahue et al. , 2014; Karpathy and Li, 2015; Fang et al. , 2015; Xu et al. , 2015) 。这类任务被称为 结构化输出任务 是因为输出值之间内部紧密相关。例如，为图片添加标题的程序输出的单词必须组合成一个通顺的句子。 |
| 异常检测 | 在这类任务中，计算机程序在一组事件或对象中筛选，并标记不正常或非典型的个体。异常检测任务的一个示例是信用卡欺诈检测。通过对你的购买习惯建模，信用卡公司可以检测到你的卡是否被滥用。如果窃贼窃取你的信用卡或信用卡信息，窃贼采购物品的分布通常和你的不同。当该卡发生了不正常的购买行为时，信用卡公司可以尽快冻结该卡以防欺诈。参考 Chandola et al. (2009) 了解欺诈检测方法。 |
| 合成和采样 | 在这类任务中，机器学习程序生成一些和训练数据相似的新样本。通过机器学习，合成和采样可能在媒体应用中非常有用，可以避免艺术家大量昂贵或者乏味费时的手动工作。例如，视频游戏可以自动生成大型物体或风景的纹理，而不是让艺术家手动标记每个像素 (Luo et al. , 2013) 。在某些情况下，我们希望采样或合成过程可以根据给定的输入生成一些特定类型的输出。例如，在语音合成任务中，我们提供书写的句子，要求程序输出这个句子语音的音频波形。这是一类结构化输出任务 ，但是多了每个输入并非只有一个正确输出的条件，并且我们明确希望输出有很多变化，这可以使结果看上去更加自然和真实。 |
| 缺失值填补 | 在这类任务中，机器学习算法给定一个新样本 x ∈ R n ， x 中某些元素 x i 缺失。算法必须填补这些缺失值。 |
| 去噪 | 在这类任务中，机器学习算法的输入是，干净样本 x ∈ R n 经过未知损坏过程后得到的损坏样本 x ˜ ∈ R n 。算法根据损坏后的样本 x ˜ 预测干净的样本 x ，或者更一般地预测条件概率分布 p ( x | x ˜) 。 |
| 密度估计或概率质量函数估计 | 在密度估计问题中，机器学习算法学习函数p model : R n → R ，其中 p model ( x ) 可以解释成样本采样空间的概率密度函数（如果 x 是连续的）或者概率质量函数（如果 x 是离散的）。要做好这样的任务（当我们讨论性能度量 P 时，我们会明确定义任务是什么），算法需要学习观测到的数据的结构。算法必须知道什么情况下样本聚集出现，什么情况下不太可能出现。以上描述的大多数任务都要求学习算法至少能隐式地捕获概率分布的结构。密度估计可以让我们显式地捕获该分布。原则上，我们可以在该分布上计算以便解决其他任务。例如，如果我们通过密度估计得到了概率分布 p ( x )， 我们可以用该分布解决缺失值填补任务。如果 x i 的值是缺失的，但是其他的变 量值 x − i 已知，那么我们可以得到条件概率分布 p ( x i | x − i ) 。实际情况中，密度估计并不能够解决所有这类问题，因为在很多情况下 p ( x ) 是难以计算的。 |

当然，还有很多其他同类型或其他类型的任务。这里我们列举的任务类型只是用来介绍机器学习可以做哪些任务，并非严格地定义机器学习任务分类。
机器学习算法可以大致分类为 无监督 （ unsupervised）算法和 监督 （ supervised ）算法。

• 无监督学习算法 （unsupervised learning algorithm）训练含有很多特征的数据集，然后学习出这个数据集上有用的结构性质。在深度学习中，我们通常要学习生成数据集的整个概率分布，显式地，比如密度估计，或是隐式地，比如合成或去噪。还有一些其他类型的无监督学习任务，例如聚类，将数据集分成相似样本的集合。
• 监督学习算法 （supervised learning algorithm）训练含有很多特征的数据集，不过数据集中的样本都有一个 标签（label）或 目标（target）。例如，Iris 数据集注明了每个鸢尾花卉样本属于什么品种。监督学习算法通过研究 Iris 数据集，学习如何根据测量结果将样本划分为三个不同品种。

以下是决定机器学习算法效果是否好的因素：

1. 降低训练误差。
2. 缩小训练误差和测试误差的差距。
   这两个因素对应机器学习的两个主要挑战： 欠拟合 （ underfitting ）和 过拟合（overfitting ）。欠拟合是指模型不能在训练集上获得足够低的误差。而过拟合是指训练误差和和测试误差之间的差距太大。

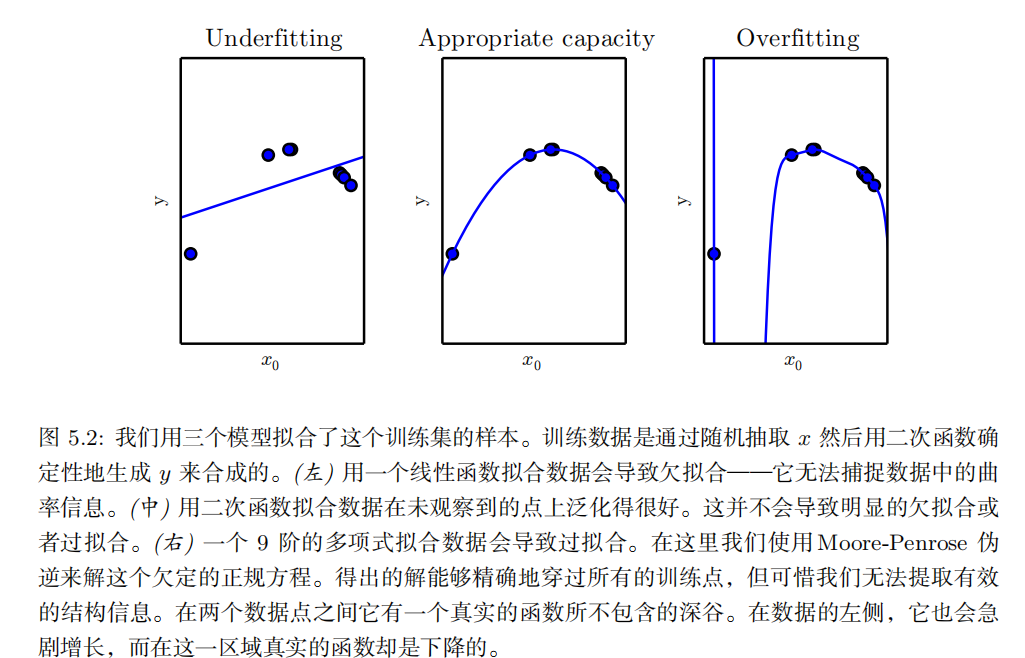
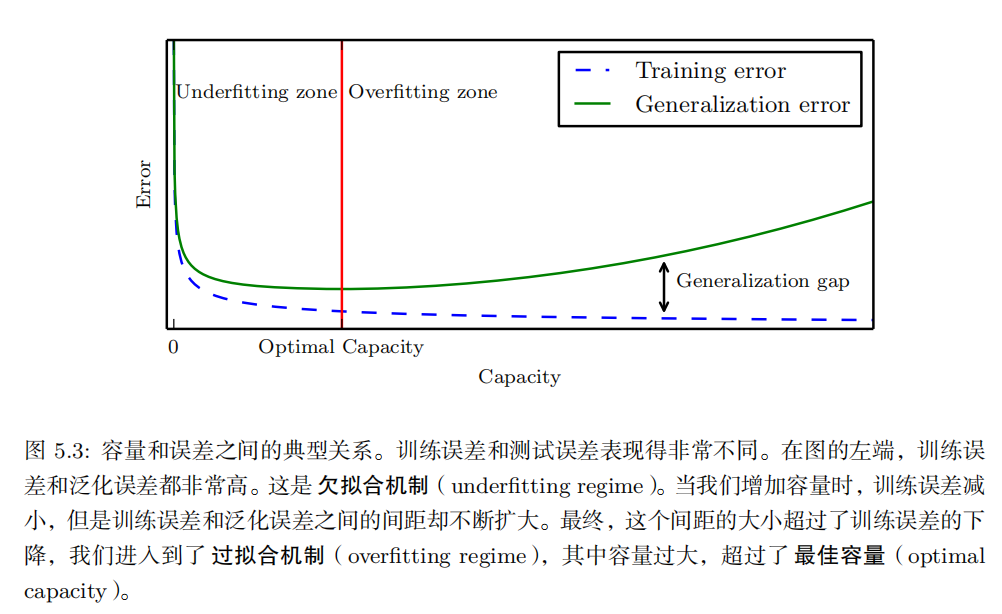
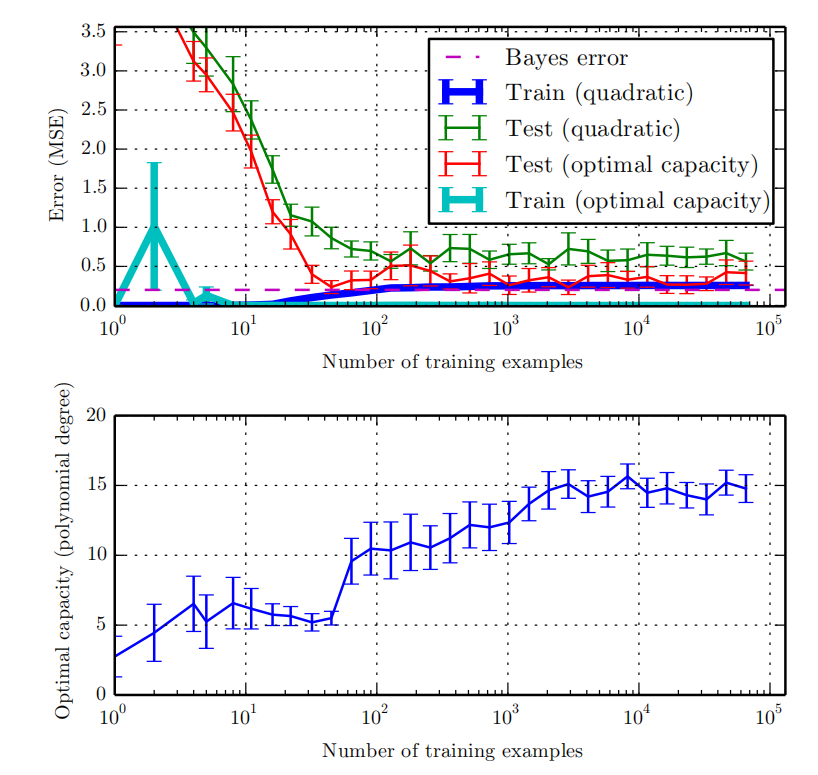
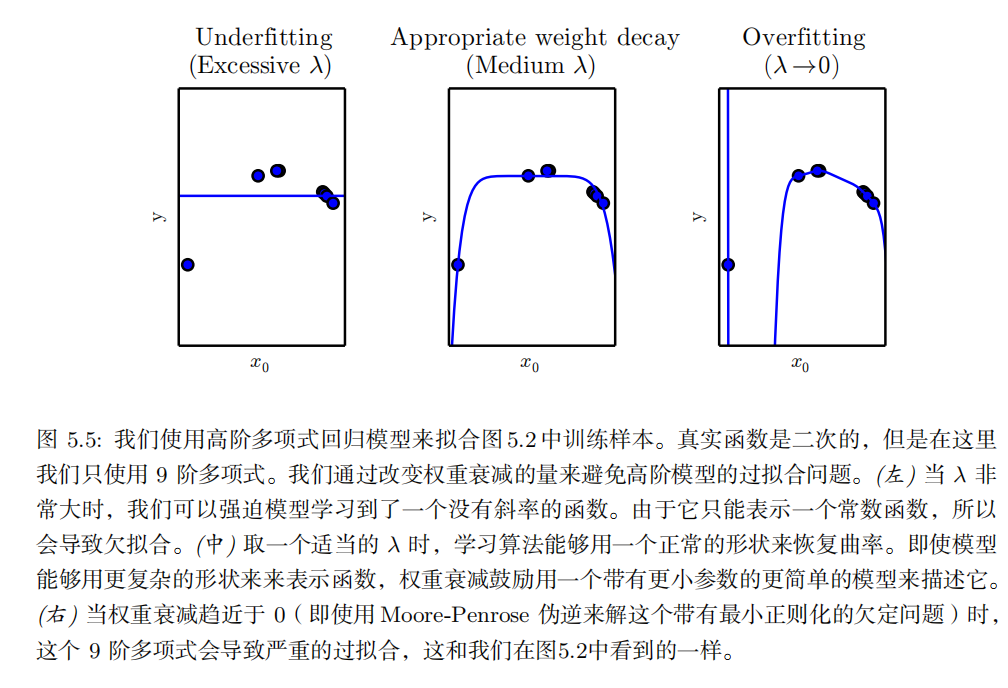
k- 折交叉验证过程，如算法 5.1 所示，将数据集分成 k 个不重合的子集。测试误差可以估计为 k 次计算后的平均测试误差。在第 i 次测试时，数据的第 i 个子集用于测试集，其他的数据用于训练集。带来的一个问题是不存在平均误差方差的无偏估计 (Bengio and Grandvalet, 2004) ，但是我们通常会使用近似来解决。

点估计 （ point estimator）或 统计量 （ statistics ）是这些数据的任意函数：

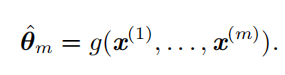
估计的偏差被定义为：

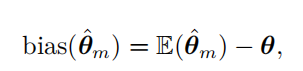
除了频率派统计 （ frequentist statistics ）方法和基于估计单一值 θ 的方法，然后基于该估计作所有的预测。另一种方法是在做预测时会考虑所有可能的 θ 。后者属于 贝叶斯统计 （ Bayesian statistics ）的范畴。
最大后验（Maximum A Posteriori, MAP）点估计

|-------------|--------------------------------------------------------------------------------------------------|
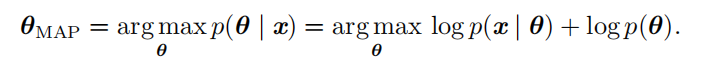
| 监督学习算法 | 概率监督学习：逻辑回归（logistic regression） |
| 监督学习算法 | 支持向量机 （ support vector machine, SVM ） |
| 监督学习算法 | 其他简单的监督学习算法： 决策树 （ decision tree ）及其变种是另一类将输入空间分成不同的区域，每个区 域有独立参数的算法 (Breiman et al. , 1984) 。 |
| 无监督学习算法 | 主成成分分析（PCA） |
| 无监督学习算法 | k - 均值聚类 |

促使深度学习发展的挑战

当数据的维数很高时，很多机器学习问题变得相当困难。这种现象被称为 维数灾难（ curse of dimensionality ）
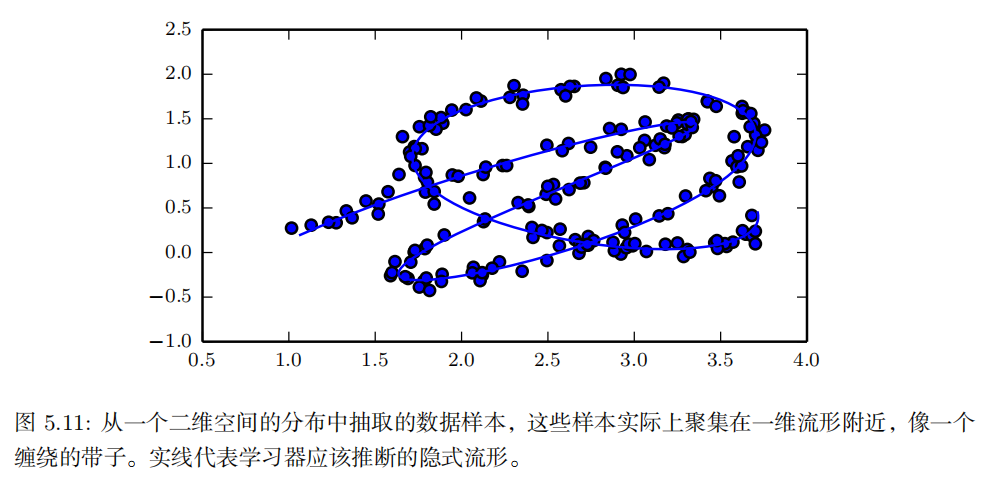
流形（manifold **）**指连接在一起的区域。数学上，它是指一组点，且每个点都有其邻域。给定一个任意的点，其流形局部看起来像是欧几里得空间。日常生活中，我们将地球视为二维平面，但实际上它是三维空间中的球状流形。