题目
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
数据范围
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同
测试用例
示例1
java
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]示例2
java
输入:nums = [0]
输出:[[],[0]]题解1(迭代,利用位运算,时间On*2n,空间On)
java
class Solution {
// curr: 用于临时存放当前正在构建的这一个子集
List<Integer> curr = new ArrayList<>();
// res: 存放最终所有子集的结果列表
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
int len = nums.length;
// 核心逻辑:遍历 0 到 2^n - 1 的所有数字
// 1 << len 等同于 2^len。例如 len=3,则 1<<3 = 8。
// mask (掩码) 的二进制形式代表了一种子集的选取状态
// 比如 mask = 5 (二进制 101),代表选中第0个和第2个元素
for (int mask = 0; mask < (1 << len); mask++) {
// 每次构建新子集前,必须清空临时列表
curr.clear();
// 遍历数组的每一位,检查它在当前 mask 中是否被"选中"
for (int i = 0; i < len; i++) {
// (1 << i) 是制造一个"探针",只有第 i 位是 1,其他位是 0
// (mask & (1 << i)) 是"按位与"操作:
// 如果结果不为 0,说明 mask 的第 i 位是 1(开关开了)
if ((mask & (1 << i)) != 0) {
// 如果开关开了,就把对应的 nums[i] 加入当前子集
curr.add(nums[i]);
}
}
// 必须使用 new ArrayList<>(curr) 创建一个新的列表对象
// 如果直接 res.add(curr),最后结果里全是空的(因为 curr 后面被 clear 了)
res.add(new ArrayList<>(curr));
}
return res;
}
}题解2(dfs,递归,时间On*2n,空间On)
java
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
// 入口:从数组的第 0 个位置开始尝试,当前的路径(子集)是空的
dfs(nums, 0, new ArrayList<>(), res);
return res;
}
/**
* @param nums 原始数组
* @param start 控制搜索的起始位置(这是"不走回头路"的关键!)
* @param curr 当前正在构建的子集路径
* @param res 结果集
*/
private void dfs(int[] nums, int start, List<Integer> curr, List<List<Integer>> res) {
// ---------------------------------------------------------
// 1. 【收集结果】(Save Snapshot)
// ---------------------------------------------------------
// 与全排列不同,子集问题中,递归树上的每一个节点(包括根节点空集)都是一个有效的结果。
// 关键点:必须使用 new ArrayList<>(curr) 进行"深拷贝"。
// 如果直接 res.add(curr),存进去的是内存地址。随着后续 curr.remove 的操作,
// 结果集里的所有列表都会变成空的。
res.add(new ArrayList<>(curr));
// ---------------------------------------------------------
// 2. 【横向遍历与纵向递归】(Explore & Backtrack)
// ---------------------------------------------------------
// i 从 start 开始:这是为了避免重复。
// 假设 nums=[1,2,3]。
// 如果当前选了 1,下一层从 2 开始选(得到 [1,2])。
// 轮到当前层选 2 时,下一层从 3 开始选(得到 [2,3])。
// 永远不会回头去选 1,所以绝不会出现 [2,1] 这种重复组合。
for (int i = start; i < nums.length; i++) {
// [做选择]:把当前数字加入路径
curr.add(nums[i]);
// [递归]:进入下一层决策树
// 关键:传入 i + 1。
// 表示:"我都选了下标为 i 的这个数了,子集里的下一个数,只能从 i 后面去找"。
dfs(nums, i + 1, curr, res);
// [撤销选择](回溯):
// 递归返回了,说明包含 nums[i] 的所有情况都找完了。
// 把 nums[i] 拿出来,好让循环继续,去试探下一个数 nums[i+1]。
curr.remove(curr.size() - 1);
}
}
}思路
这道题的思路没什么可以讲解的,特别是dfs,很容易想到,就是很平常的一个回溯深搜。但迭代思路如果没接触的话确实不容易想到这么做(比如博主),所以博主这里贴一下迭代思路就行了。
记原序列中元素的总数为 n。原序列中的每个数字 ai的状态可能有两种,即「在子集中」和「不在子集中」。我们用 1 表示「在子集中」,0 表示不在子集中,那么每一个子集可以对应一个长度为 n 的 0/1 序列,第 i 位表示 ai是否在子集中。例如,n=3 ,a={5,2,9} 时:
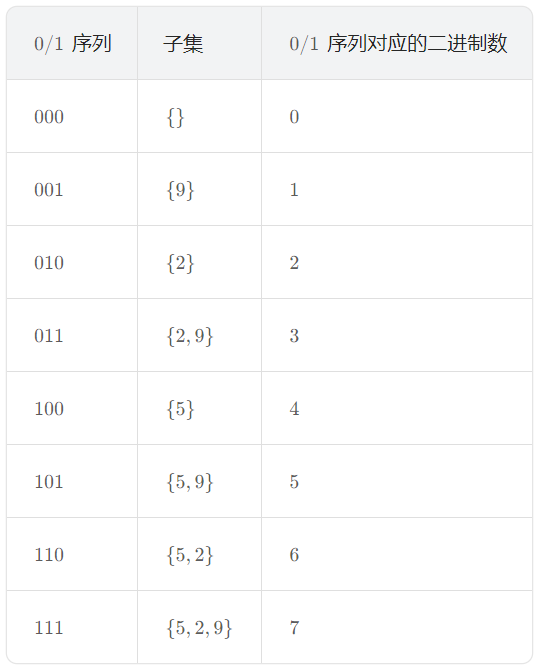
可以发现 0/1 序列对应的二进制数正好从 0 到 2n −1。我们可以枚举 mask∈[0,2n −1],mask 的二进制表示是一个 0/1 序列,我们可以按照这个 0/1 序列在原集合当中取数。当我们枚举完所有 2n个 mask,我们也就能构造出所有的子集。