1 Sigmoid 函数
这是最经典的激活函数,模拟了生物神经元的"开"与"关"。
公式
原函数: σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
导数: σ ′ ( x ) = σ ( x ) ⋅ ( 1 − σ ( x ) ) \sigma'(x) = \sigma(x) \cdot (1 - \sigma(x)) σ′(x)=σ(x)⋅(1−σ(x))
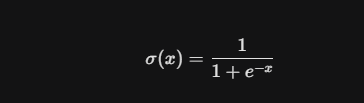
- x x x:输入的特征值。
- e e e:自然常数,负责产生平滑的指数增长/衰减。
- − x -x −x:负号确保了当 x x x 很大时, e − x e^{-x} e−x 趋近于 0 0 0,结果趋近于 1 1 1;反之趋近于 0 0 0。
- 1 + ... 1 + \dots 1+...:分母始终大于 1 1 1,确保输出范围在 ( 0 , 1 ) (0, 1) (0,1) 之间。
为什么要这么做?
优点(体现在原公式中):
- 归一化 :输出永远在 ( 0 , 1 ) (0, 1) (0,1),在公式中表现为分母永远比分子大一点点。这让它 天然适合做门控信号(控制多少信息通过)。
缺点(体现在导数中):
-
梯度消失 :看导数公式 σ ( x ) ( 1 − σ ( x ) ) \sigma(x)(1-\sigma(x)) σ(x)(1−σ(x)),当 x = 0 x=0 x=0 时,导数达到最大值 0.25 0.25 0.25。这意味着每经过一层 Sigmoid 激活,梯度至少衰减 75%。在深层网络(如 32 层的 MiniMind)中,梯度会迅速趋近于 0,导致无法训练。
-
非零中心(Non-zero centered) :输出全是正数,这会导致下一层神经元的输入发生偏移,减慢收敛速度。
为什么非零中心有问题?
Sigmoid 函数的输出是非负数(0,1),这导致模型梯度更新方向一致 ,导致"之字形"更新路径。
例子:
假设某一层使用 Sigmoid 激活,其输出 (a_i > 0) 全为正。那么下一层神经元的输入为:
- z ( l + 1 ) = ∑ i w i ( l + 1 ) a i ( l ) + b ( l + 1 ) z^{(l+1)} = \sum_i w_i^{(l+1)} a_i^{(l)} + b^{(l+1)} z(l+1)=∑iwi(l+1)ai(l)+b(l+1)
在反向传播时,损失对权重的更新为:
- w i ← w i − η ⋅ ∂ L ∂ w i w_i \leftarrow w_i - \eta \cdot \frac{\partial \mathcal{L}}{\partial w_i} wi←wi−η⋅∂wi∂L
根据梯度链式法则,可知:
- ∂ L ∂ w i = ∂ L ∂ z ⏟ 上游梯度 ⋅ x i ⏟ 输入 \frac{\partial \mathcal{L}}{\partial w_i} = \underbrace{\frac{\partial \mathcal{L}}{\partial z}}{\text{上游梯度}} \cdot \underbrace{x_i}{\text{输入}} ∂wi∂L=上游梯度 ∂z∂L⋅输入 xi
结果:
因为所有 Sigmoid 输出 > 0,所以:
- 如果上游梯度 ∂ L ∂ z \frac{\partial \mathcal{L}}{\partial z} ∂z∂L 是 正的 ,那么 所有 ∂ L ∂ w i \frac{\partial \mathcal{L}}{\partial w_i} ∂wi∂L 都是正的 → 所有权重都往减小方向更新。
- 如果上游梯度是 负的 ,那么所有偏导都是负的 → 所有权重都往增大方向更新。
结论: 同一层的 所有权重 在一次更新中要么全增大,要么全减小,无法独立调整不同权重的方向(如:(x1, x2, x3, ...))。 每次操作的都是所有权重 。
- 如果输入 x i x_i xi可正可负的话,则代表激活值的输出为可正可负的(如 tanh 或标准化后的 ReLU),那么不同权重的偏导符号可能不同,每个权重可以根据自己的输入特征,独立选择更新方向!
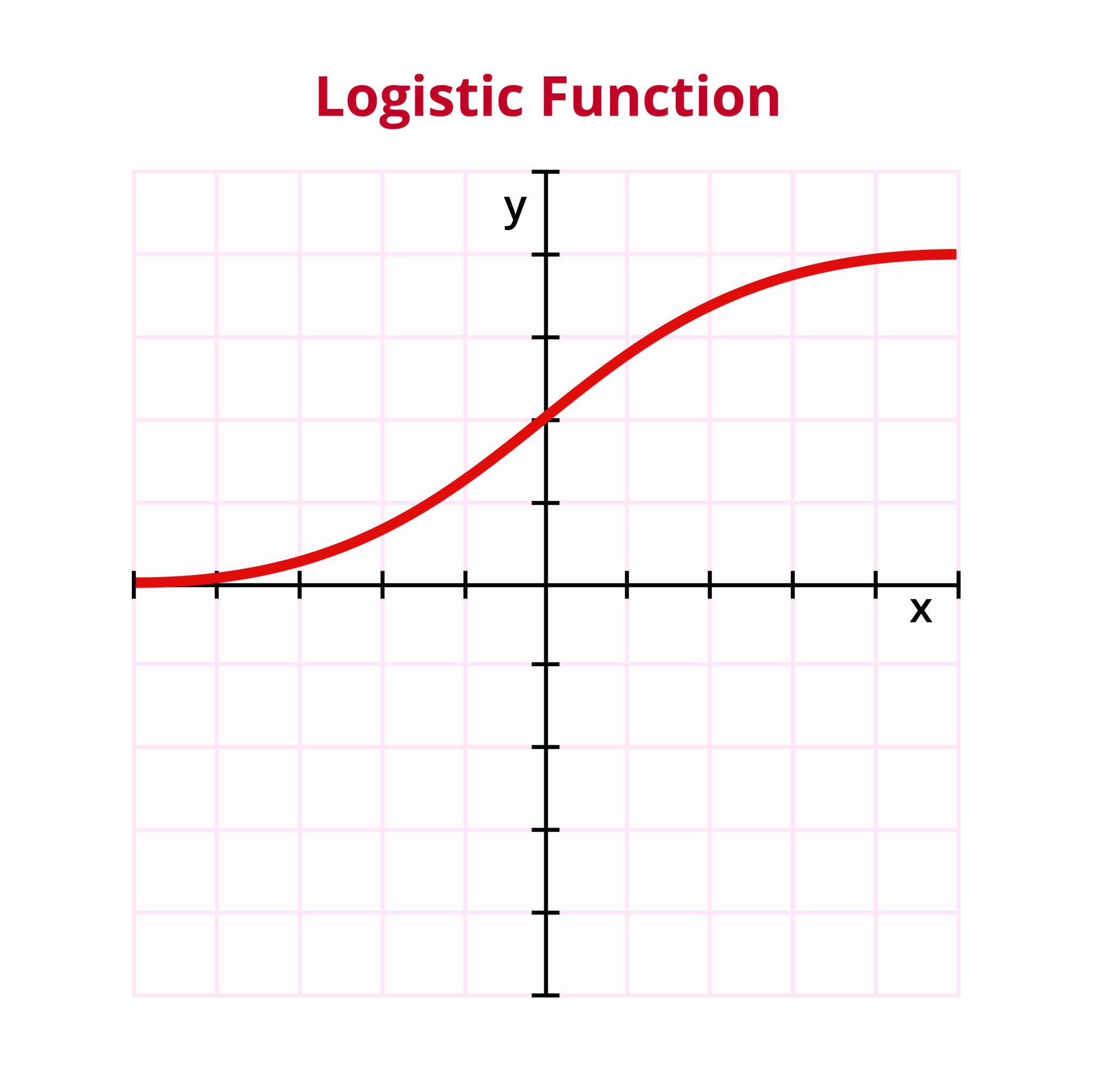
2 SiLU(Swish)平滑的"自适应门" 函数
公式
- 原函数: f ( x ) = x ⋅ σ ( x ) = x 1 + e − x f(x) = x \cdot \sigma(x) = \frac{x}{1 + e^{-x}} f(x)=x⋅σ(x)=1+e−xx
- 导数: f ′ ( x ) = σ ( x ) + x ⋅ σ ( x ) ( 1 − σ ( x ) ) = σ ( x ) ( 1 + x ( 1 − σ ( x ) ) ) f'(x) = \sigma(x) + x \cdot \sigma(x)(1 - \sigma(x)) = \sigma(x) \left( 1 + x(1 - \sigma(x)) \right) f′(x)=σ(x)+x⋅σ(x)(1−σ(x))=σ(x)(1+x(1−σ(x)))
为什么这么做?
优点(体现在原公式中):
- 无上界(Unbounded above) :当 x → ∞ x \to \infty x→∞ 时, f ( x ) ≈ x f(x) \approx x f(x)≈x,即正无穷。这保证了在高激活区域导数接近 1,有效缓解梯度消失。
f(x)=x⋅σ(x),当 x→+∞, σ(x)→1⇒f(x)≈x,所以它近似线性增长,导数也趋近于 1(见下文导数公式)。
✅ 高激活区域梯度不衰减 → 更利于深层网络传递有效梯度 → 缓解梯度消失问题。
✅ SiLU 的大值在反向传播时,不仅不会梯度消失,反而能够很好地表示激活强度
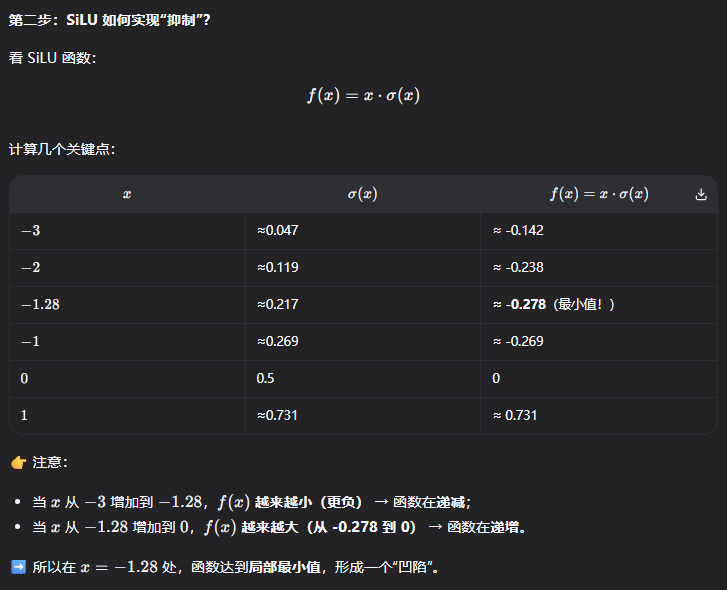
- 非单调性(Non-monotonicity) :这是 SiLU 的精髓。在 x ≈ − 1.28 x \approx -1.28 x≈−1.28 时有一个极小值。这意味着模型可以学到 "稍微抑制负值,而不是像 ReLU 那样直接杀掉它" 。
解释:
"非单调性"本身不是目的,而是实现 "灵活抑制负输入" 的数学手段。因为 SiLU 是非单调的(有极小值),所以它能在某些负区间输出比两侧更小的值 → 实现"选择性抑制"。
什么是"抑制负值"?"抑制" ≠ "归零",而是 让输出比线性情况更小(甚至为负),以表达"这个特征不太重要/可能是干扰"。但又不能完全丢弃(像 ReLU 那样),因为某些负值可能携带有用信息(如边缘对比、相位等)。
例子:SiLU 如何实现"抑制"?

优点(体现在导数中):
- 自门控梯度 :导数包含 x x x 项,意味着梯度不仅取决于激活状态 f(x),还 取决于输入值的大小 。这让模型 在反向传播时能更精细地调整权重 。
3 GELU 函数
GELU (发音为 "gel-you")是一种平滑、非单调、无上界 的激活函数,由 Dan Hendrycks 和 Kevin Gimpel 在 2016 年提出。它被设计为 ReLU 的概率化、平滑替代品,并在 BERT、GPT 等大模型中成为默认激活函数。
公式

GELU ( x ) = x ⋅ Φ ( x ) \text{GELU}(x) = x \cdot \Phi(x) GELU(x)=x⋅Φ(x);
- Φ ( x ) \Phi(x) Φ(x) 是标准正态分布的累积分布函数(CDF)
- Φ ( x ) = 1 2 [ 1 + − erf ( x 2 ) ] \Phi(x) = \frac{1}{2} \left[ 1 + - \operatorname{erf}\left( \frac{x}{\sqrt{2}} \right) \right] Φ(x)=21[1+−erf(2 x)];
为什么?

非零中心:激活值覆盖全范围,梯度更新灵活覆盖每一个权重,而不是全部权重。非单调:能够选择性抑制要求,对某些特定范围的负输入,输出比"更负"的输入还要小 ------ 这只有非单调函数才能做到。
非单调为什么能实现选择抑制?
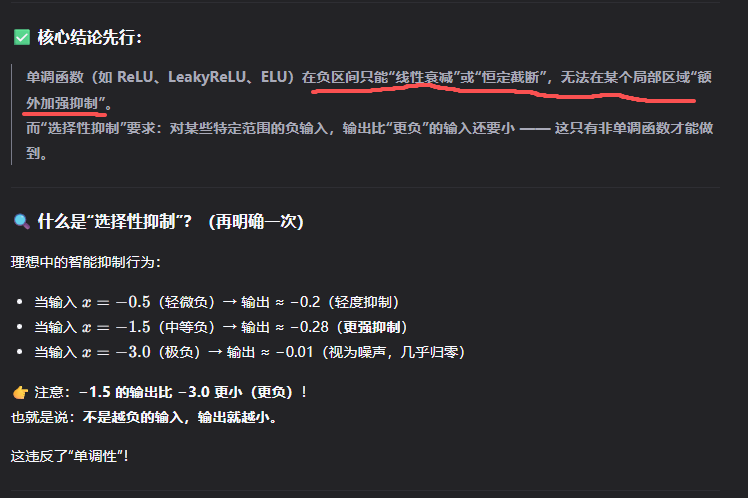
选择性抑制为什么是好处?

4 Swiglu 函数

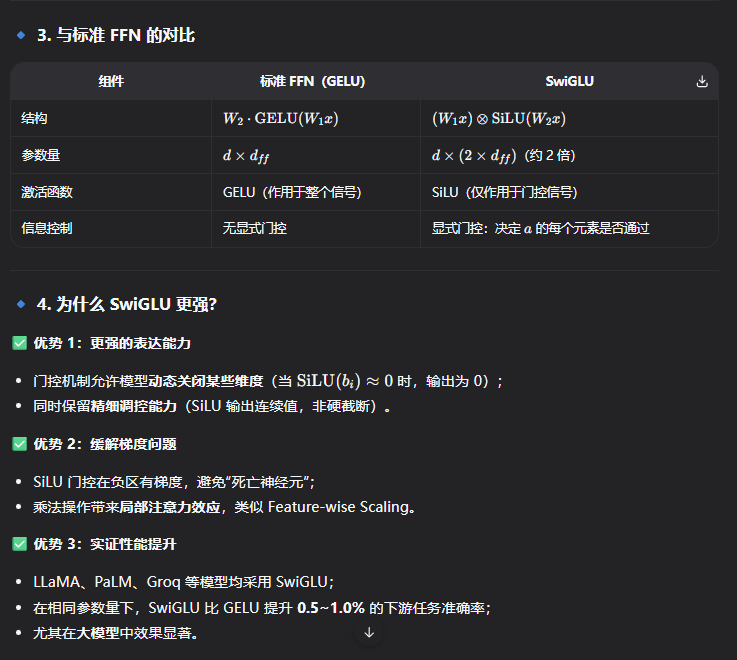

5 GeGLU 函数


