NO.1一个线性回归模型 - 用colab的第一步

colab.research.google.com/?hl=zh-cn

以下所有程序都在这个上面实现

1 参数优化与训练数据量

训练数据的使用方式：

• Batch Size: 每次训练时模型观察的数据量称为batch size，例如每次只给模型看10个数据样本
• 更新次数: 若有1万个数据，batch size=10，则需要更新参数1000次（10000/10）
• 数据量不足的表现: 若更新1000次后模型效果仍不佳，可能是数据量太小或学习率设置不当

数据重复使用的注意事项

• 常规做法: 训练时每条数据通常只看一遍，避免过拟合（类比"刷题过多导致看什么都像原题"）
• 特殊情况处理:
  当模型在特定任务（如数学题）表现不佳时，可重复使用相关训练数据
• 实际案例：千问、DeepSeek等大模型在特定场景下也会采用此方法
  注意：这是"没办法的办法"，应谨慎使用

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

• ​NumPy​: 数值计算基础库
• ​Pandas​: 数据处理库
• ​Matplotlib​: 数据可视化库
• ​train_test_split​ : 用于划分训练集和测试集
  导入技巧
• ​自动补全​: 输入部分代码后，Colab会自动提示完整导入语句
• ​环境优势​: 网页端无需配置本地环境，开箱即用

2 线性回归代码实现：类的初始化与参数更新

2.1 类的基本结构

①

• ​学习率​: 默认设为0.01
• ​迭代次数​: 默认设为1000次

② - ​​梯度计算​ ​:

• d w = 1 m X T ( y p r e d − y ) dw = \frac{1}{m}X^T(y_{pred} - y) dw=m1XT(ypred−y)

• d b = 1 m ∑ ( y p r e d − y ) db = \frac{1}{m}\sum(y_{pred} - y) db=m1∑(ypred−y)

• ​​参数更新​​:

  • w = w − α ⋅ d w w = w - \alpha \cdot dw w=w−α⋅dw
  • b = b − α ⋅ d b b = b - \alpha \cdot db b=b−α⋅db

• ​​归一化处理​​: 除以self.m（样本数量）使梯度更稳定

• 编程规范建议

  • ​面向对象编程​: 将功能封装成类（如Transformer架构也采用此方式）
  • ​代码组织​ :
    • 初始化方法(init)设置基本参数
    • 核心算法逻辑单独封装
    • 预测方法(predict)独立实现

class LinearRegression:
	def __init__(self, learning_rate=0.01, n_iters=1000):
    self.lr = lr
    self.iterations = iterations
  def update_weight(self):
    y_hat = self.predict(self.X) # y帽是预测值，通过输入x得到预测值

    # 求对dw的梯度
    dw = - (2 * (self.X.T).dot(self.Y - y_hat)) / self.m
    db = - 2*np.sum(self.Y - y_hat) / self.m  # 这里的m是进行平均化

    self.w = self.w - self.lr * dw
    self.b = self.b - self.lr * db
    return self

  def forward(self, X, Y):
    # 前传函数
    # m 样本数量，n特征数量
    self.m, self.n = X.shape # X为一个3*4的矩阵
    self.w = np.zero(self.n)

    self.b = 0
    self.X = X
    self.Y = Y

    # 1000个轮次
    for i in range(self.iterations):
      self.update_weight()

    return self

  def predict(self, X):
    return X.dot(self.w) + self.b

2.2主要运行程序（main）

2.2.1线性回归代码实现：前传函数与预测

• forward函数规范：深度学习模型中前传过程统一命名为forward，这是行业编码规范
• shape属性：矩阵的内置函数，返回维度元组。如3×4矩阵调用x.shape返回(3,4)
• 参数初始化：
  样本数量m和特征数量n通过x.shape获取
  权重采用零初始化w = np.zeros(n)
  偏置项同样初始化为0 b = 0
• 向量化操作：处理批量数据时将多条数据拼接成向量，如每次处理10条数据则构造长度为10的向量
• 梯度下降实现：
  iterations参数表示参数更新轮次（深度学习中也称step）
  每个iteration完成一次参数更新
• 预测函数：实现的线性方程y = wx+b，其中w为权重向量，b为偏置项

2.2.2线性回归代码实现：数据读取与预处理

• 数据上传：在Colab中通过文件上传功能将数据上传到当前工作目录
• 数据格式处理：
  支持多种格式（csv/json/txt等）
  实际编码时可通过AI辅助完成格式转换
• 示例数据集：工作年限与薪资的预测数据
• 数据集划分：
  使用train_test_split划分训练集和测试集
  test_size=0.2表示20%数据作为测试集
  随机筛选保证数据分布一致性

# 读取数据
df = pd.read_csv('YearsExperience_Salary.csv')
X = df.iloc[:,:-1].values  # 未来可直接跟ai说，我要把一个什么文件转成为可以训练的格式，用来读取
Y = df.iloc[:,-1].values
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

2.2.3 线性回归代码实现：模型训练与预测

• 模型初始化：需指定learning_rate和iterations两个超参数
• 训练过程：
  调用forward函数传入特征向量x和标签向量y
  自动完成参数更新过程
• 结果展示：
  预测值输出使用np.round保留2位小数
  可对比前3条数据的预测值和真实值
  可视化测试集数据点和回归线
• 调试技巧：
  利用Colab的自动补全功能提高编码效率
  通过报错信息定位问题所在
  逐步验证各模块功能

model = LinearRegression(lr=0.01,iterations=1000)


#进行训练
model.forward(X_train, Y_train)

# 在testset上进行一次预测，看预测准不准
Y_pred = model.predict(X_test)

#看一下预测结果
print("预测值：",np.round(Y_pred[:3],2))
print("真值：",Y_test[:3])

# 计算均方误差
mse = mean_squared_error(Y_test, Y_pred)
print("均方误差：",mse)

2.2.4线性回归代码实现：结果可视化与调试

数据可视化方法：

• 将真实值和预测值同时绘制在二维坐标系上，横轴表示工作经验年限，纵轴表示预测薪资
• 绘图流程：
  先绘制真实数据点（散点图）
  再绘制预测结果线（直线图）
  通过对比观察拟合效果

代码调试技巧

• 常见错误处理：
  变量名错误：如报错信息显示"变量未定义"，需检查变量名拼写是否一致
  函数调用错误：注意类方法调用时是否遗漏self参数
• 调试步骤：
  阅读报错信息第一层（如model.forward报错）
  追踪到具体报错代码行
  检查相关变量定义和使用
  修改后重新运行验证

# 可视化
plt.scatter(X_test, Y_test, color='blue', label='Test Data')
plt.plot(X_test, Y_pred, color='orange', label='Prediction')
plt.xlabel('years of Experience')
plt.ylabel('Salary')
plt.legend()
plt.show()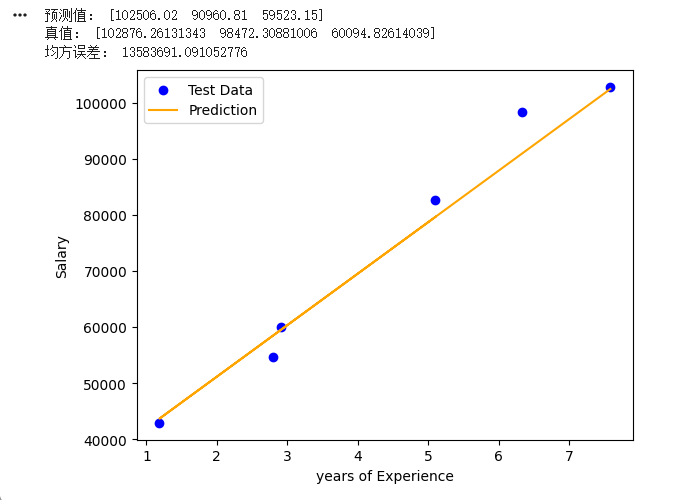

2.3 模型训练核心逻辑 及现代开发选择

初始化要点

• 所有类必须包含 __init__ 方法
• 权重W和偏置b初始化为零（使用np.zeros）

训练流程

• 前向传播：固定命名为forward方法

权重更新

核心是通过数学推导得到的梯度更新公式：
d w = − 2 n X T ( Y − Y ^ ) dw = -\frac{2}{n} X^T (Y - \hat{Y}) dw=−n2XT(Y−Y^)
d b = − 2 n ∑ ( Y − Y ^ ) db = -\frac{2}{n} \sum (Y - \hat{Y}) db=−n2∑(Y−Y^)

• 迭代优化：每个iteration更新一次参数

---

开发工具与环境

开发工具使用技巧

Colab使用建议

• 分段执行代码（Jupyter Notebook特性）
• 开启自动补全功能提高效率

开发环境选择

• 小型模型：Colab免费版足够
• 大型模型：需使用专业平台如AutoDL

---

现代开发模式

• 重点聚焦理论创新而非代码实现
• 实际开发中多借助AI代码生成工具
• 工程师核心竞争力转向理论深度和领域见解

---