λ(lambda)不是一个"新物理量",而是 Smith 遮蔽模型里的一个中间统计函数 。
它的意义可以一句话概括:
λ(v) 表示:在给定观察/光照方向 v 下,一个微表面法线被其它微表面遮挡的"期望遮挡程度"。
λ 的物理含义(直观层)
在微表面模型里,你假设表面是由大量微小镜面(microfacets)组成的。
当你从方向 v 看过去,并不是所有"朝向合适"的微表面都能被看到:
-
有些被旁边更高的微表面挡住(masking)
-
有些在入射方向上被挡住(shadowing)
λ(v) 表示:沿方向 v,平均有多少"潜在可见微表面"被挡掉了。
-
λ = 0:几乎无遮挡(法线接近正对)
-
λ 大:遮挡严重(grazing 视角)
它不是概率本身,而是一个用于构造概率的统计量。


"从方向 v 看过去,微表面坡度在该方向上的平均陡峭程度是多少。"
λ 是连接"法线统计 (D)"与"可见性 (G)"的桥梁。
各向异性粗糙度在切线平面上本质是一个椭圆尺度张量,而它的两个主轴参数自然就记为 αx、αy。


为什么是 x/y?
因为在推导里,切线空间通常写成局部坐标:
-
x 轴:tangent(T)
-
y 轴:bitangent(B)
-
z 轴:normal(N)
所以各向异性参数写成:
-
αx:沿 x(切线)方向
-
αy:沿 y(副切线)方向
这是局部坐标系约定,不是世界坐标。
历史来源:Walter / Heitz / Disney 统一命名
从各向异性 GGX 的经典文献开始,符号就是:
-
αx, αy:椭圆分布尺度
-
Λ(v):Smith 遮蔽统计
-
D(h):NDF
例如:
-
Walter et al. 2007(GGX/Trowbridge-Reitz)
-
Heitz 2014(Smith Joint / VNDF)
-
Disney BRDF 2012(anisotropic roughness)
这些论文都采用 αx、αy 作为主轴参数。
所以引擎代码沿用:
-
Unreal:AlphaX / AlphaY
-
Unity HDRP:roughnessT / roughnessB → alphaT / alphaB
-
Filament:at, ab
ax/ay 是最短的工程写法。

椭圆度量(anisotropic metric)

切线平面变成椭圆缩放:
所以 denom 就是:把 h 在切线平面按 αx/αy 拉伸后,再计算它的平方长度

物理意义:它控制"这种法线出现的概率"
NDF 的作用是:
给定一个半程向量 h,这种微表面法线出现的概率密度是多少?
-
如果 h 落在椭圆主轴方向上,并且对应粗糙度大 → denom 小 → D 大
-
如果 h 落在细轴方向上 → denom 大 → D 小
因此:
-
denom越小,高光越集中(概率密度越高) -
denom越大,高光越弱(概率密度越低)
平方让分布衰减更慢,比 Beckmann 更"长尾",这就是 GGX 更真实的原因(尤其 grazing)。
为什么还要加 NoH²?
很多人第一次看会疑惑:
为什么切线项除以 α²,而法线项不除?
denom 是"半程向量在各向异性粗糙度椭圆下的距离平方",决定 D(h) 的衰减。
denom 和 Lambda 里的 tan2
同一个椭圆度量在 h-space 与 v-space 的两个投影版本--->GGX D 和 Smith G 能闭合
-
"h-space 投影"(半程向量 H 在 T/B/N 上的投影)
这是给 D(h) 用的,也就是你
D_GGX_Aniso()的这段:
-
ToH = dot(T,H), BoH = dot(B,H), NoH = dot(N,H)
-
denom = (ToH²)/αx² + (BoH²)/αy² + NoH²
-
D = 1 / (π αx αy denom²)
直观含义:把 H 看成一个方向,问"这个 H 在椭圆分布下出现的概率密度是多少"。所以它天然是 "h-space"。
-
"v-space 投影"(视线 V / 光线 L 在 T/B/N 上的投影)
这是给 Smith 的遮蔽/阴影(Λ(v)、Λ(l))用的,你
Lambda_GGX_Aniso()里是:
-
ToV = dot(T,V), BoV = dot(B,V), NoV = dot(N,V)
-
tan²θ_v(aniso) = (ToV²)/αx² + (BoV²)/αy² 然后再除以 NoV²
-
Λ(v) = ( -1 + sqrt(1 + tan²θ_v) ) / 2
直观含义:Smith G 描述的是"沿着某个出射方向 v,微表面自遮蔽的统计",所以它必须以 v 为自变量(v-space)。同理对 l 也做一次,然后 joint 组合。
同一个数学对象(各向异性 GGX)在代码层面有两种等价写法/投影写法
各向异性--[ggx,ggx是一种数学对象
d项和光照和视角无关
但 H 是由 L 和 V 共同决定的 ,因此从"复合依赖"角度讲,D 会随光照和视角变化------不是因为它"看 L/V",而是因为 H 变了。
1.0 / (PI * ax * ay * denom * denom)为什么可以精准的表示一种离散样本的统计情况?
D在描述"无限多微表面法线样本的概率密度极限"。

(1) "统计模型/分布"指的是我们用一个连续概率密度去描述微表面法线的随机性;
(2) "蒙特卡洛采样"指的是用有限样本去数值估计积分。
D(h)=1/(π ax ay denom²) 属于第 (1) 类,不是"积分后的结果",也不依赖"样本无限"这个前提;它本身就是连续分布的解析表达(概率密度/面积密度)。
真正"需要积分"的地方在哪里
需要积分的是最终的镜面反射能量(渲染方程):


积分等于 1,而不是 D(m) 的取值在 [0,1]
概率密度函数(PDF)一样:PDF 在某些点的值完全可以大于 1,只要整体积分为 1 就行。
因此 D(h) 可以远大于 1,尤其在粗糙度很小(α 很小)且 h 接近法线时,会出现尖峰(这也是你要 clamp roughness/α 的原因之一)。
你可以把它直观地理解成:
"同一个全局 H,在切线平面里投影到 T/B 方向后,分别按 αx、αy 缩放,最后形成一个'椭圆度量'下的长度平方;GGX 用这个椭圆度量的长度来决定该方向出现的概率密度。"
ax,ay并不是离开了ggx 就完全没有意义,离开 microfacet 分布族与其配套的 G/采样/IBL 处理,才算的是失去可比性
一个椭圆度量下的"长度平方"。这类结构不仅 GGX 用,Beckmann/Gaussian、Phong 的某些各向异性形式也有类似"两个轴尺度"的参数。换句话说:
- ax/ay 的可解释性来自"这是一个各向异性 NDF 的主轴尺度参数"
改用 Beckmann,各向异性的 D 仍会用 αx、αy(但公式不同);它们仍然是"切线平面两个主轴的 roughness 参数",只是对应的尾部行为不同。
"GGX"并不是一个单独的 BRDF,而是一个微表面统计族里的一种 NDF(D 项)选择。
你完全可以在 Cook--Torrance 框架里替换 D 项,只要你同时保证 G(Smith)与之匹配,或者明确接受近似。
Cook--Torrance 的结构允许替换 D
"用 GGX"严格来说是:
-
D = GGX (Trowbridge--Reitz)
-
G = Smith-GGX(与 GGX 分布一致)
-
采样与 LUT 也通常围绕 GGX
但你可以换掉 D。
新艺术时期


维梅尔 Johannes Vermeer (楊·維梅爾)
黑键提供"天然的手指弧度"。
例子:
Db 大调:大量黑键,手型自然贴合
F# 大调:拇指更容易落白键支撑
C 大调:全白键,反而容易手塌
所以 Chopin 才会说:
"最自然的音阶是 B 大调。"
这不是玄学,是人体工学。
Smith Joint 的几何项 G(以及 Vis)是"方向相关的遮蔽函数",它定义在入射方向 L 和视线方向 V 上,而不是定义在半角向量 H 上。

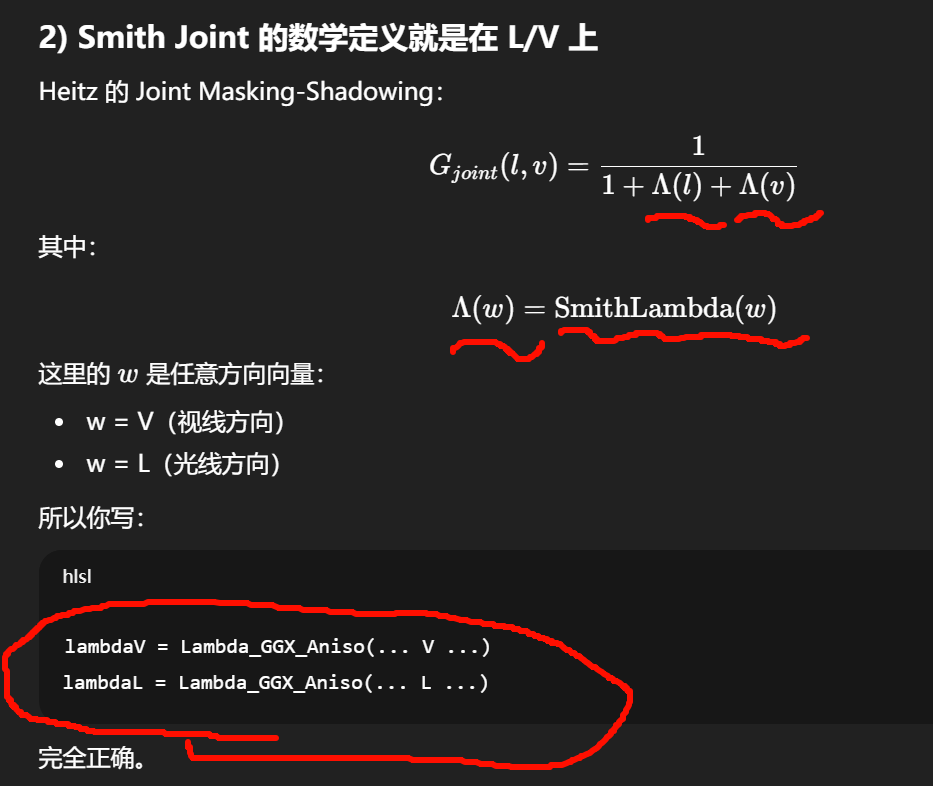
几何项的物理意义是:
-
从方向 V 看进去,微表面有多少被遮挡(masking)
-
从方向 L 打进来,微表面有多少投影被阴影遮住(shadowing)
这两件事只与 入射方向和出射方向有关,不与 H 有直接定义关系。
如果你用 H 代替 V 或 L,会导致:
-
grazing 区域遮蔽不正确
-
能量不守恒
-
高光边缘会异常亮或异常暗
Λ 的意义可以理解成:从某个方向 w 看过去,由微表面统计导致的"额外遮挡程度"的量化。角度越 grazing(NoW 越小),Λ 越大,G 越小。
为什么是这个开方形式
这是 GGX(Trowbridge-Reitz)分布下,Smith masking-shadowing 函数的一个常用闭式近似/闭式形式。对于 GGX,几何衰减随角度的变化不像 Beckmann 那样指数衰减,而是具有更重尾(heavy tail),于是会出现这种 的结构。
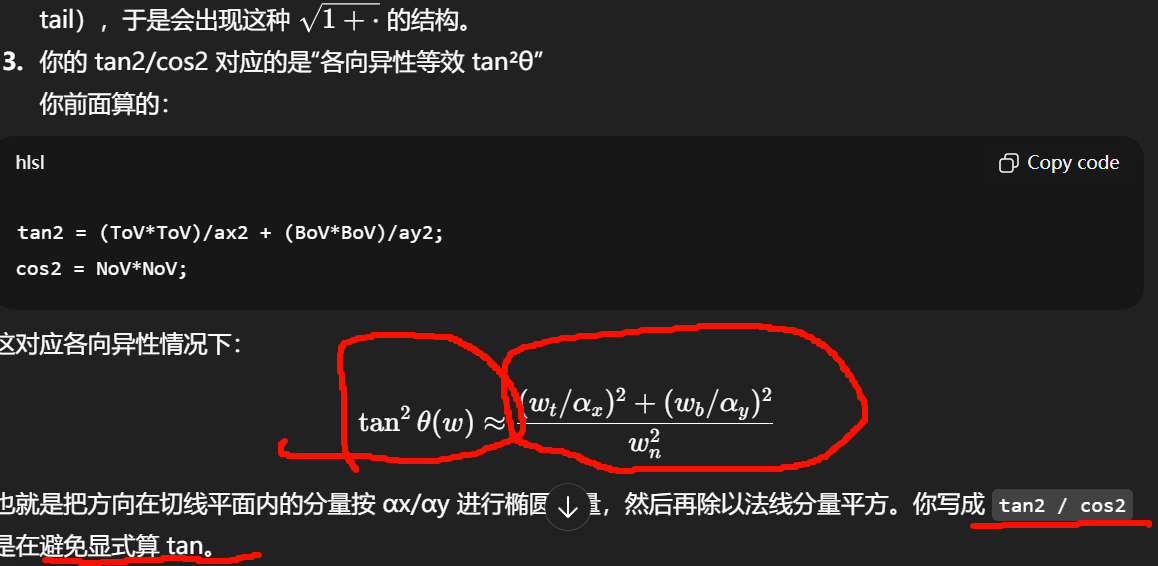
"避免显式算 tan"

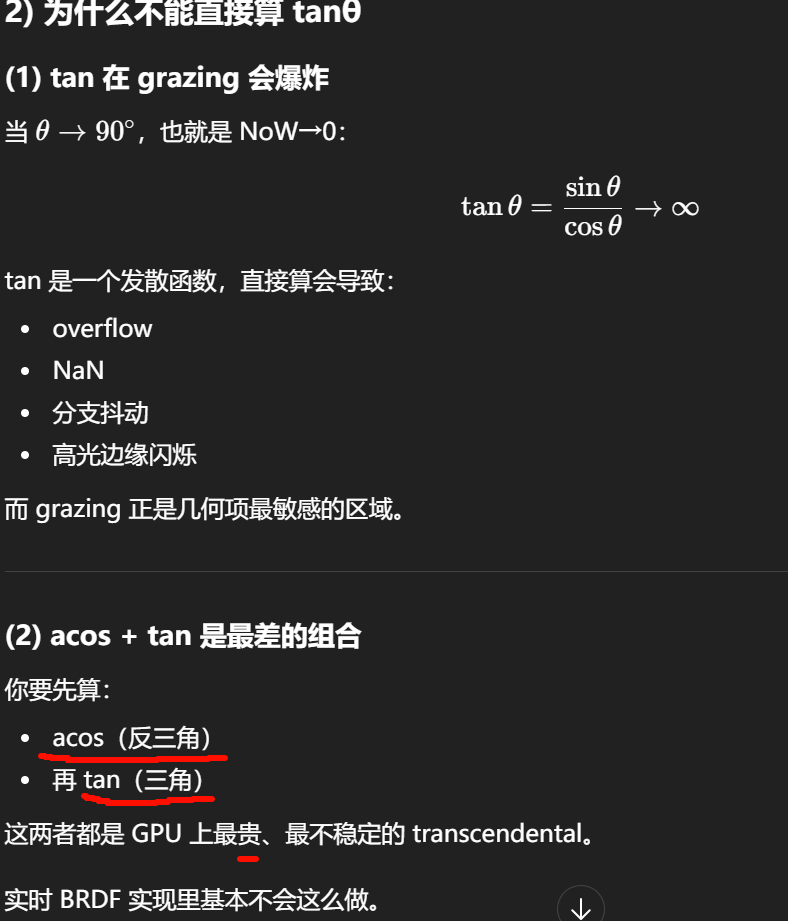

在各向异性 GGX 中,切线平面不是欧式长度,而是椭圆度量:
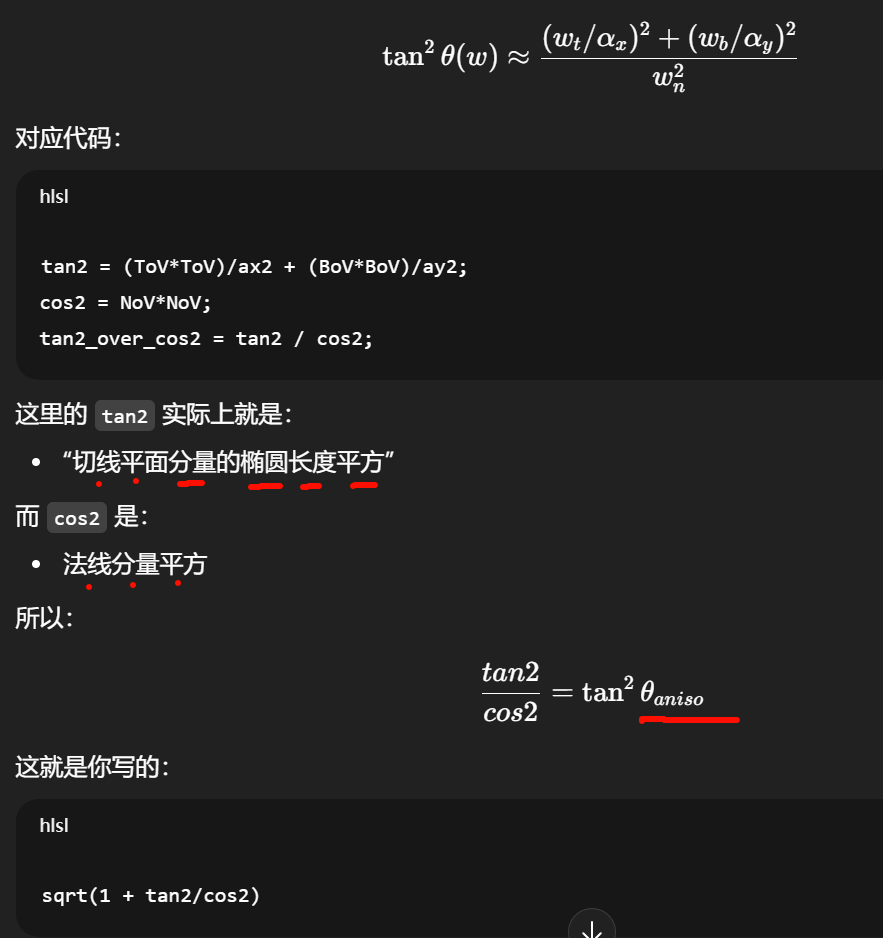

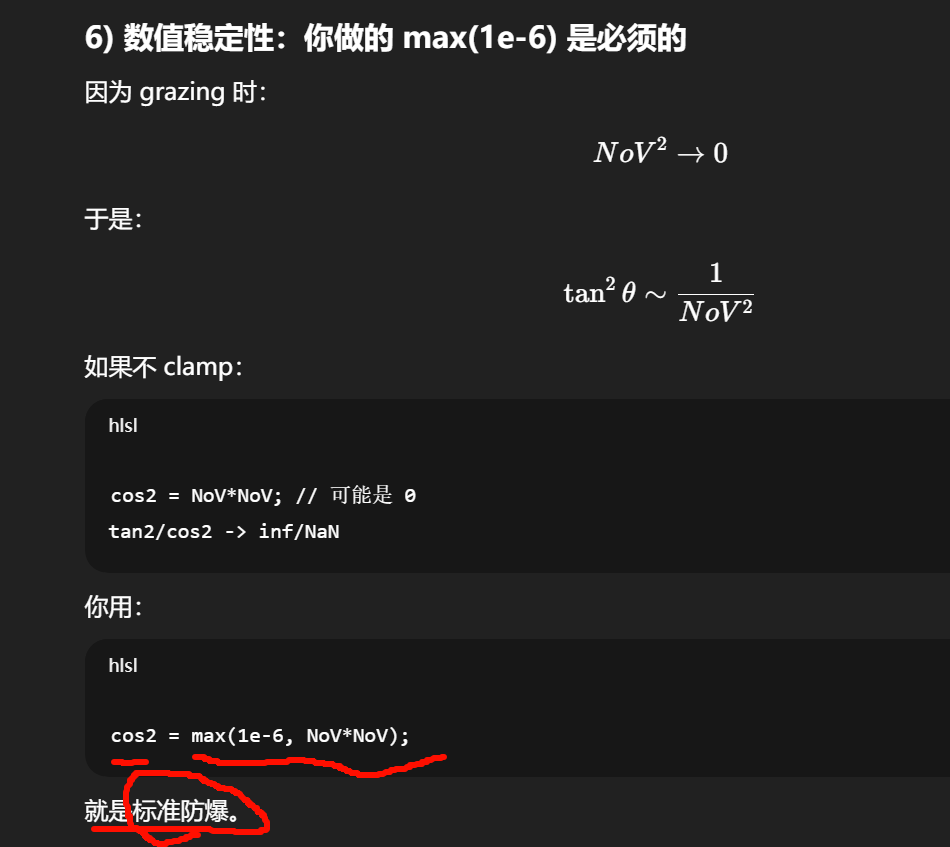
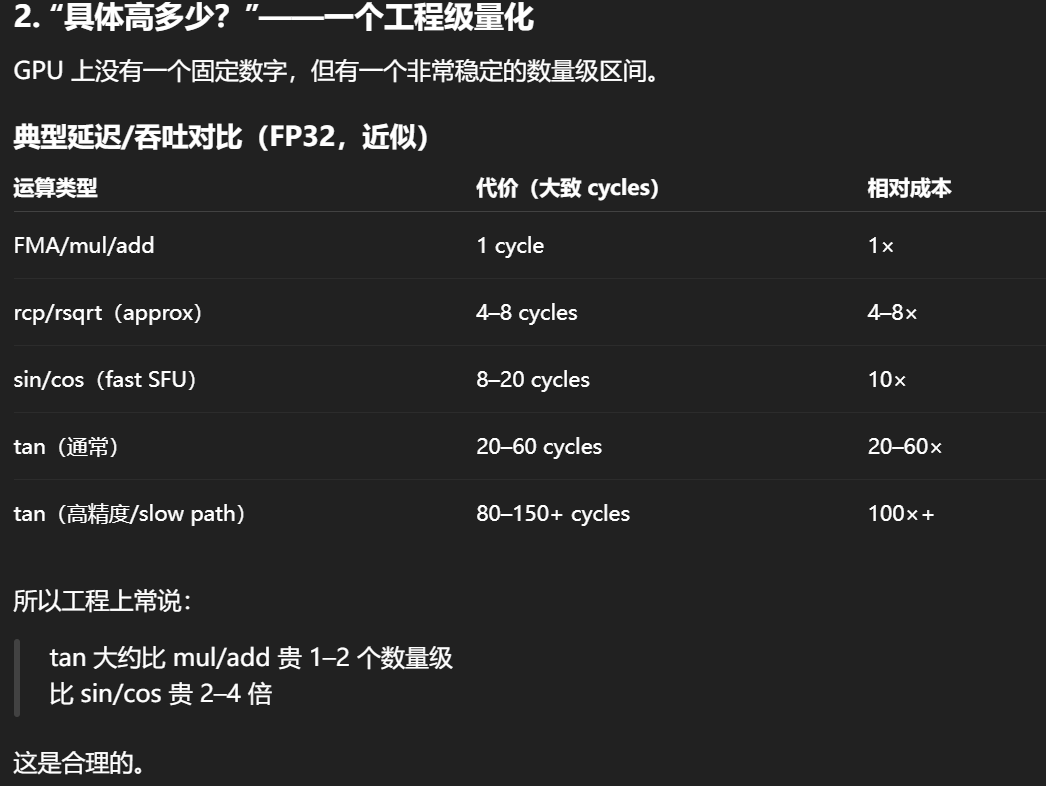

实际 profiling 怎么验证?
你如果想要"具体高多少"在你的 pipeline 上成立,唯一可靠方法是:
microbenchmark shader
-
baseline:纯 FMA loop
-
variant:插入 tan()
-
用 Nsight / Radeon GPU Profiler / RenderDoc capture
观察:
-
SFU utilization
-
instruction latency
-
warp occupancy stall
这才是精确答案。

-
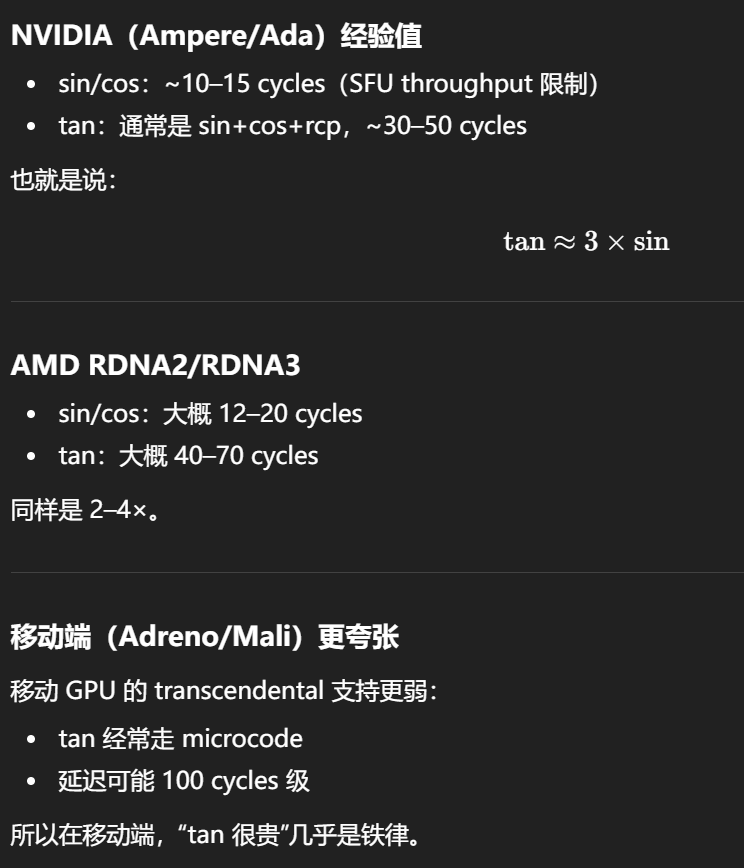
GPU 上 tan 消耗高的原因是:它不是基本指令,需要 range reduction + sin/cos + division,并且在 π/2 附近数值病态导致 slow path。
-
定量上:tan 通常比 mul/add 贵 20--60×,比 sin/cos 贵 2--4×,移动端可能达到 100×。
-
是否"真的贵"取决于调用频率:每像素、每光源循环里使用会非常明显。
Range Reduction 是什么?
三角函数是周期函数:sin(x) 周期 2π
tan(x) 周期 π
tan(x)=tan(x+kπ)
这意味着:
对任意输入角度 xxx,我们都可以先把它"折叠"回一个小区间,再去做近似计算。
这个"折叠回主区间"的过程就是 range reduction。
实现会拆成:2/π=C1+C2+C3
用多次 FMA 减去,保证余数 rrr 精度够。
这叫 Payne--Hanek reduction 或 Cody--Waite reduction。
这一步不是简单 mod,而是高精度浮点算法。

GPU Shader 中的实际情况
HLSL/GLSL 的 tan()
一般会调用硬件 SFU 或 microcode:
-
内部必定包含 reduction
-
输入越大 reduction 越慢
-
某些架构在大输入时走 slow path
这就是为什么 shader 编程里常见经验:
Avoid transcendental functions unless you know input range.
正入射附近(NoV≈1, NoL≈1)
此时 ToV、BoV 很小,tan2/cos2 很小:
λV ≈ 0,λL ≈ 0
=> G ≈ 1/(1+0+0)=1
=> Vis ≈ 1/(4 NoV NoL) ≈ 1/4
"Vis ≤ 1/4"只在一个很特殊的点成立:NoV=NoL=1 且 λ≈0(也就是 V、L 都正对法线、遮蔽近乎没有):
G≈1,Vis≈1/(4*/*1)=1/4。
roughness → α → D 与 G 的形状
AO 与 DV 的关系:理论无关,工程上通常只作用于 IBL
AO(ambient occlusion)不是 BRDF 参数,它不属于 Cook--Torrance。
DV 是微表面统计模型,AO 是宏观遮蔽近似。
因此:
-
AO 不应直接乘在 direct specular 上
-
AO 常用于环境光项(IBL)
常见做法:
indirectDiffuse *= ao; indirectSpecular *= SpecularAO(ao, roughness, NoV);
其中 SpecularAO 通常是启发式:
float specAO = saturate(pow(NoV + ao, roughness));
目的:
-
避免凹槽里反射环境光过亮
-
但 direct lighting 不受影响
-
DV_SmithJointGGX_Aniso 定义的是 specular BRDF 的微表面统计结构(D+G/Vis)
-
roughness 决定 DV 的输入 αx/αy(高光宽度与遮蔽)
-
metallic 不改变 DV,只决定 Fresnel F0 与 diffuse/specular 能量分配
-
AO 与 DV 理论无关,工程上只用于环境光遮蔽,不应直接影响 direct specular
c_diff = (1 - metallic) * albedo
这对应标准 metallic workflow:
metallic 控制 diffuse/specular 的能量分裂
| metallic | diffuse | specular F0 |
|---|---|---|
| 0 | 有漫反射 | F0≈0.04 |
| 1 | 无漫反射 | F0=albedo |
正确应是:
float3 kd = (1.0 - F) * (1.0 - metallic);
float3 diffuse = kd * albedo / PI;
否则会发生什么?
-
正视角:F≈0.04,diffuse 基本没问题
-
grazing:F→1,但 diffuse 仍然保持全强
-
结果就是 grazing 会过亮,不守恒
所以 diffuse 这一行目前是"不完整 PBR"。
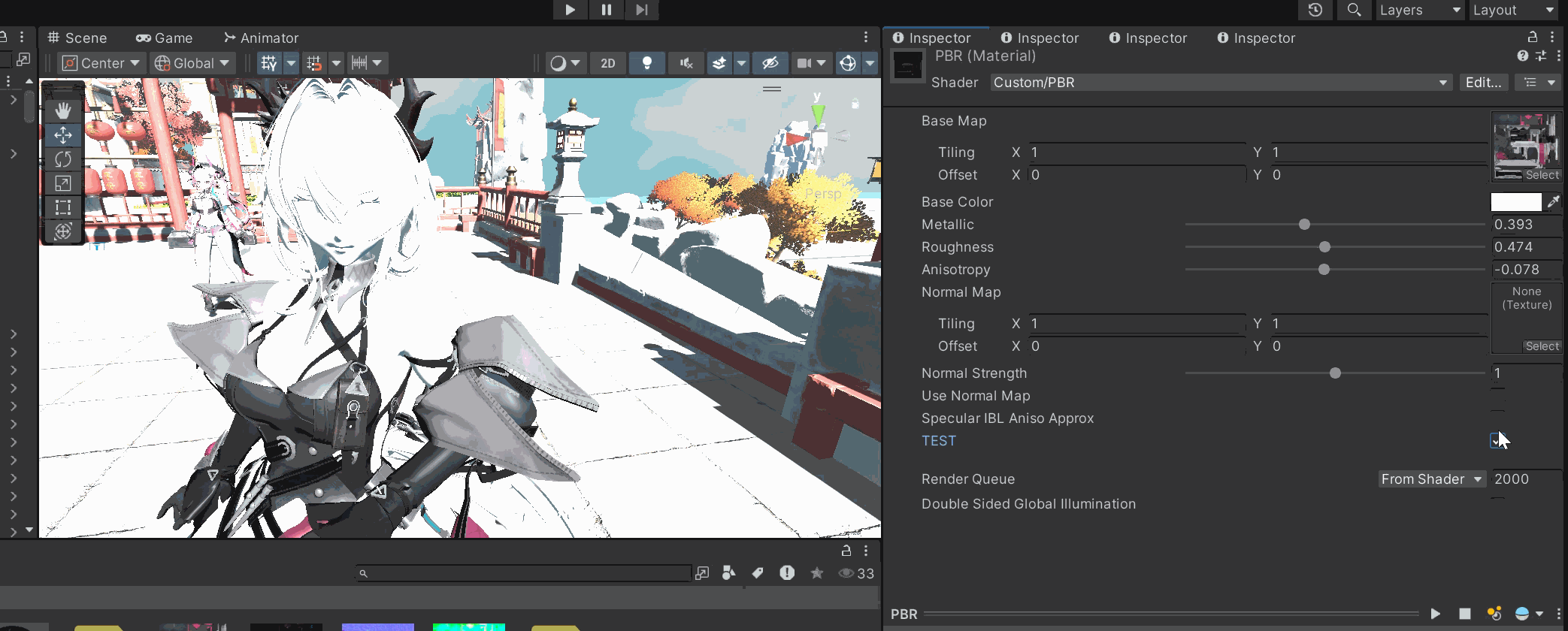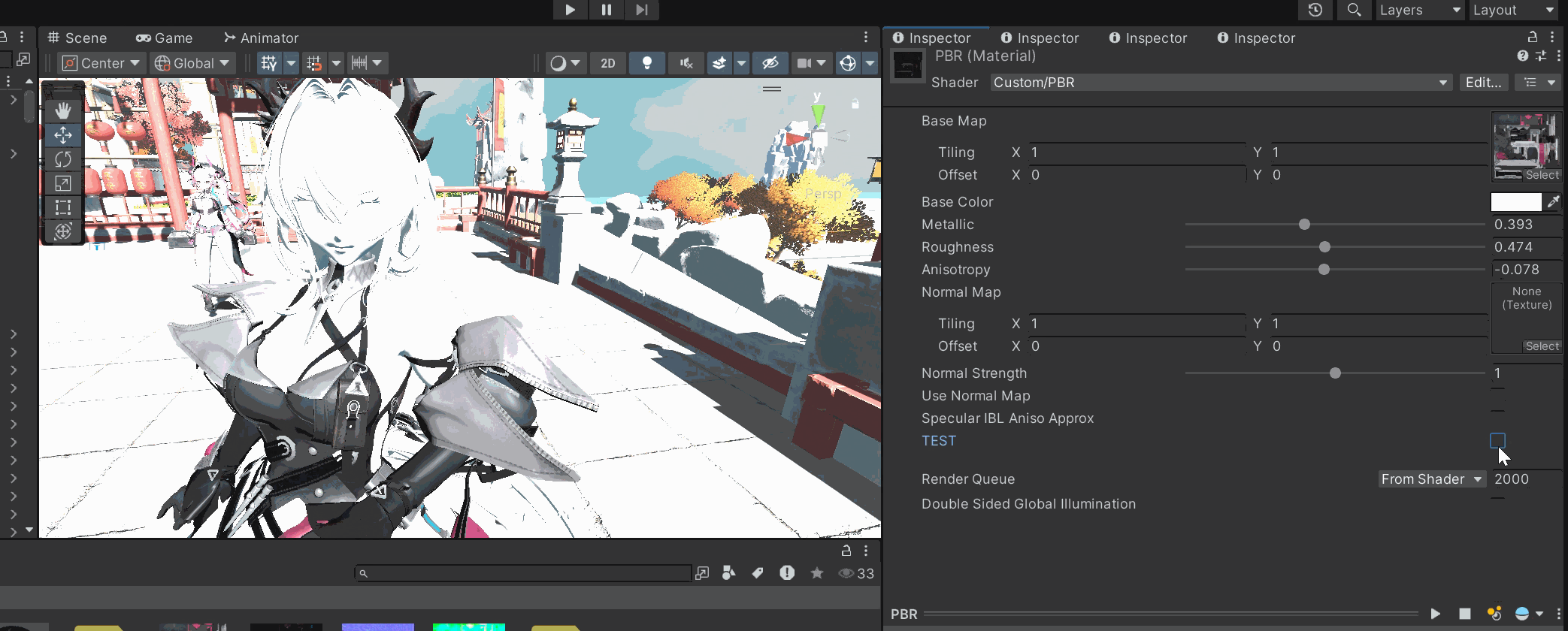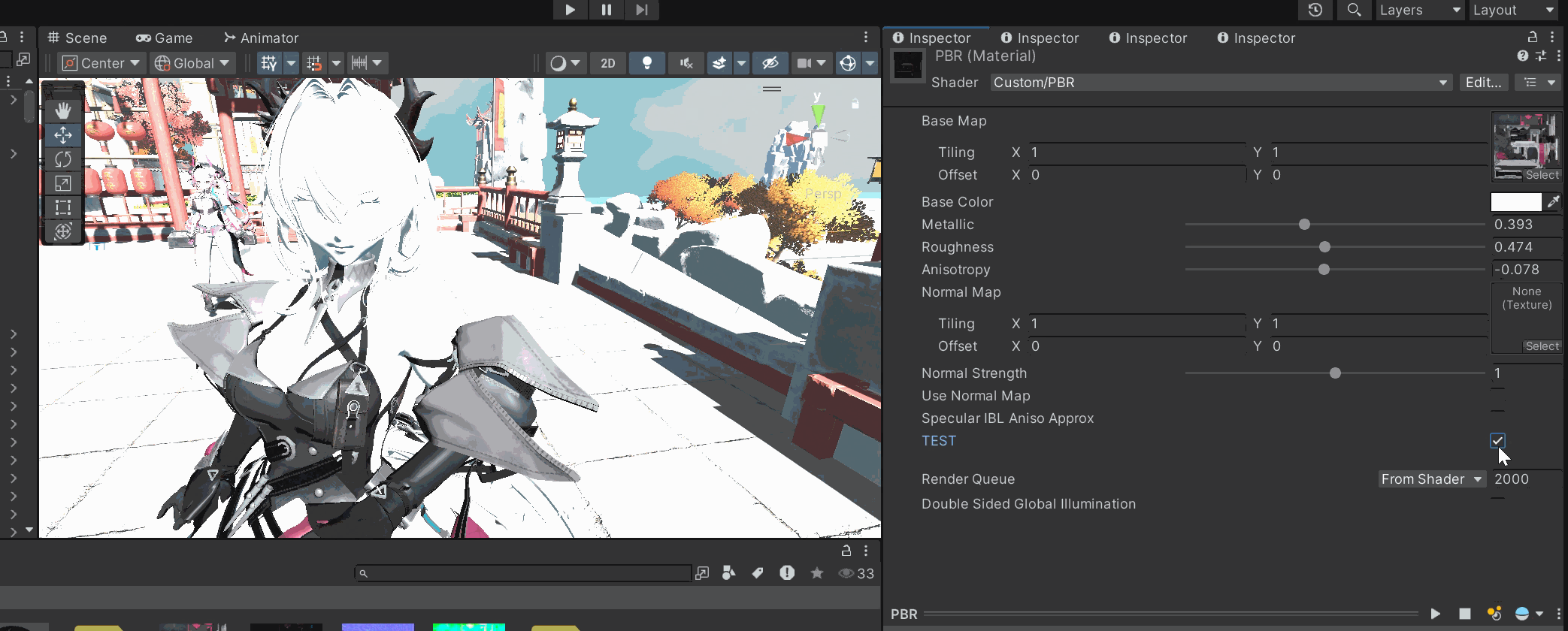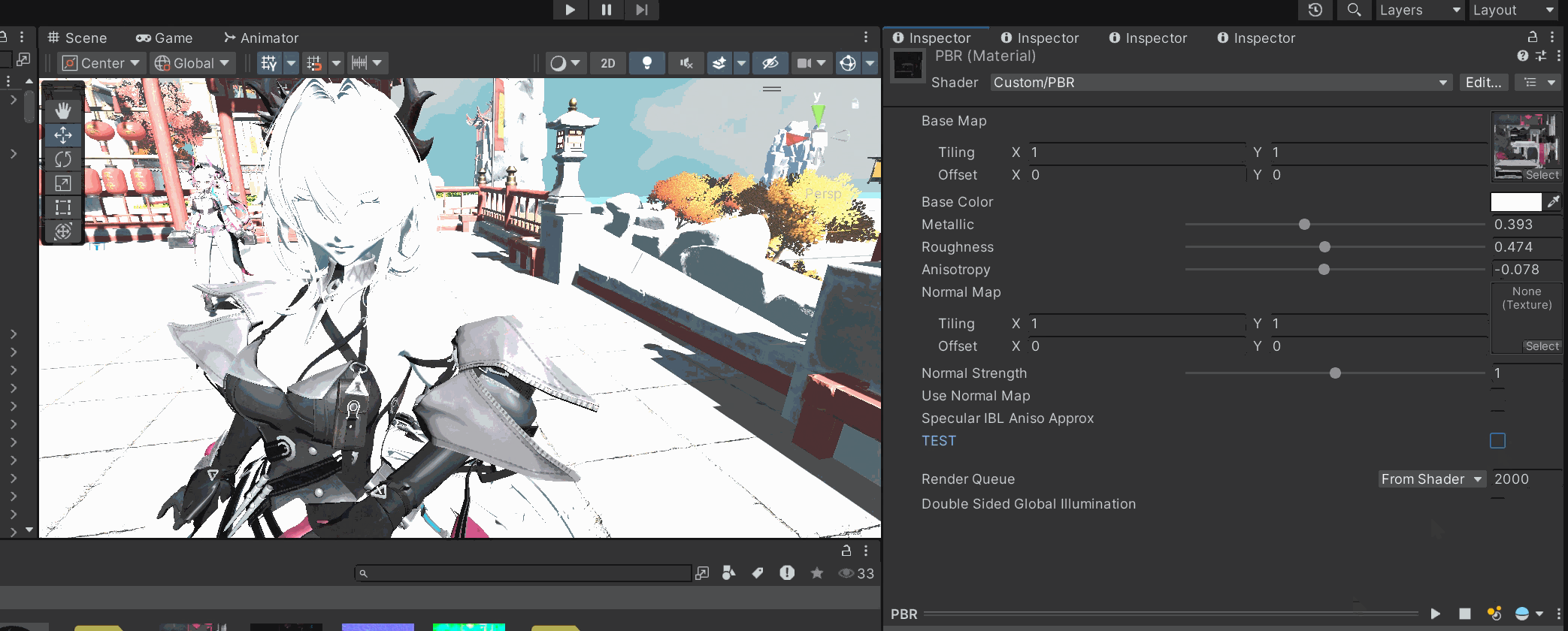
cpp
float3 f0 = lerp(0.04, albedo.rgb, saturate(_Metallic));
float3 F = F_Schlick_local(f0, VoH);
float3 specular = D * Vis * F;
float3 kd = (1.0 - F) * (1.0 - _Metallic);
float3 diffuse = kd * albedo.rgb * (1.0 / PI);
if (_TEST < 0.5)
diffuse = (1.0 - _Metallic) * albedo.rgb * (1.0 / PI);其实差别不大,一个是为了能量守恒把漫反射的能量额外消减了,看上去可能会保守一点,更加的"温顺",如果没有额外的要求的情况下,我还是更喜欢狂野一点的数值暴力。
所以我选择还是遵守Diffuse能量的消减
cpp
float3 radiance = mainLight.color * mainLight.distanceAttenuation * mainLight.shadowAttenuation;
float3 color = (diffuse + specular) * radiance * NoL;* NoL,本质上不是"材质能量守恒项",而是渲染方程里的几何投影项(cosine law / Lambert 余弦定律)。它描述的是:同样的入射辐亮度 Li 打到一个倾斜表面时,单位表面面积接收到的辐照度(irradiance)会按 cosθ 变小。这跟 BRDF 自身是否能量守恒是两件不同层级的事,但它们在同一条公式里同时出现,所以很容易混在一起。

-
radiance≈ Li(包含距离衰减、阴影、光色等) -
(diffuse + specular)≈ fr -
NoL≈ (n⋅l)
NoL 是"入射几何项",把 radiance 转成 irradiance(接受能量随倾角减少)
渲染方程(反射):
这里的(n⋅l) 就是你代码里的 NoL。

"Tashika datta kke" (確かだったっけ) in Japanese means "If I remember correctly, was it [X]?" or "Was it true/certain?".
Breakdown of the Phrase
- Tashika (確か): Certain, sure, reliable, or if I remember correctly.
- Datta (だった): Was (past tense of da / desu).
- Kke (っけ): A sentence-ending particle used for retrieving or recollecting previously shared information.
Based on the Japanese phrasing, "Ikiteta desho" (生きてたでしょ) most commonly means "They/he/she were/was alive, right?" or "It was still alive, wasn't it?".
Here is a breakdown of the phrase:
- Ikiteta (生きてた): A colloquial, casual past tense form of ikiteiru (to be living/alive). It means "was alive" or "was living".
- Desho (でしょ): A conversational, shortened form of deshou. It acts as a tag question, meaning "isn't it?", "right?", or "don't you agree?".
"Haka made itte" could roughly be interpreted in Japanese as "Going to the grave" or "Saying [something] until the grave" (often implying keeping a secret forever or doing something until death).
- Haka made (墓まで): Means "Until the grave" or "To the grave".
- Itte (行って/言って): Means "Going" (from iku ) or "Saying" (from iu).
"Kaeshite hoshii" (返してほしい / かえしてほしい) in Japanese means " I want [you] to return it " or "I want [it] back".
The Shader decides "how to interpret the material", while the texture decides "what the material actually is".
最常见的最小集合(游戏量产默认)
-
BaseColor (sRGB)
-
Normal (切线空间,通常BC5/ATI2,线性)
-
ORM 或分离的:Occlusion、Roughness、Metallic(线性;经常打包到一张纹理 RGB)
你大概率能拿到这些,但细节不一定规范(例如 roughness 是否是 perceptual,normal 是否是 DirectX/GL 约定)。
经常"拿不到但很想要"的
-
Height/Displacement(很多项目不做)
-
Bent Normal、Thickness、Curvature(烘焙成本高、工具链不统一)
-
Anisotropy/Aniso direction(更少,尤其在非高端管线)
典型从高模到引擎的链条:
-
高模/低模 + UV
-
Bake:Normal/AO/Curvature/Thickness 等(MikkTSpace 一致性是重点)
-
在 Substance Painter / Designer 里用 PBR 模板绘制
-
导出预设(Unreal/Unity/自定义)→ 贴图命名与通道打包
-
引擎导入:色域、压缩、通道语义、法线翻转、金属度约定
你应重点盯住三件事:
-
切线空间一致性(MikkTSpace + 正确的 tangent sign)
-
色域/线性空间(baseColor sRGB,其他一律线性)
-
粗糙度/光滑度约定(roughness vs smoothness;是否 perceptual;是否要平方到 alpha)
输入契约(你向美术/外包明确写清楚的规范)
至少要在文档里明确:
-
BaseColor:sRGB,禁止含光照/阴影/高光;++金属 baseColor 允许带色(导体反射色)++
-
Metallic:++0/1 为主++ ,允许++少量过渡++;线性
-
Roughness:线性(perceptual roughness),范围[0,1],禁止反相;引擎内部 alpha = roughness²
-
Normal:MikkTSpace;DirectX 还是 OpenGL 绿通道约定(必须定死)
-
ORM 打包顺序:例如 R=AO, G=Roughness, B=Metallic(或你项目的顺序)
-
强制贴图命名/后缀(便于导入器识别)
MikkTSpace 解决的是"切线基(TBN)怎么定义"
MikkTSpace规定了如何从 UV/几何计算 tangent、bitangent(以及 tangent.w 的 handedness)。这保证你在 bake(Substance/xNormal/Marmoset 等)和引擎运行时使用同一个 tangent 生成规则时,normal map 的细节方向一致,接缝和镜像 UV 处理一致。
-
只要 bake 端和引擎端都用 MikkTSpace(或兼容实现),就不会出现"同一张 normal 在接缝处左右不一致"的大问题。
-
Unity(尤其 URP/HDRP)常见工作流默认就是 MikkTSpace(依赖模型导入 tangent),但你仍要确保 DCC 导出的 tangents 与引擎计算方式一致(或干脆让引擎重算,且 bake 端按同样方式)。
-
DirectX vs OpenGL 绿通道约定解决的是"normal map 编码的坐标系方向"
切线空间 normal 通常存的是 (x,y,z) = (T方向,B方向,N方向) 的分量,贴图里一般:
-
R = x
-
G = y
-
B = z(或由 x,y 重建)
差异只在 y(绿通道)的符号:
-
"DirectX normal":y 向上(常见理解:+Y 指向 bitangent 的某一方向)
-
"OpenGL normal":y 取反(相当于把 B 轴反过来)
很多工具链把它描述成:OpenGL 相对 DirectX 需要 flip green(G = 1 - G 或 y = -y)。本质就是切线空间的 handedness/轴向约定不同导致的编码差异。