Leecode热题100：矩阵置零（矩阵）

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例：

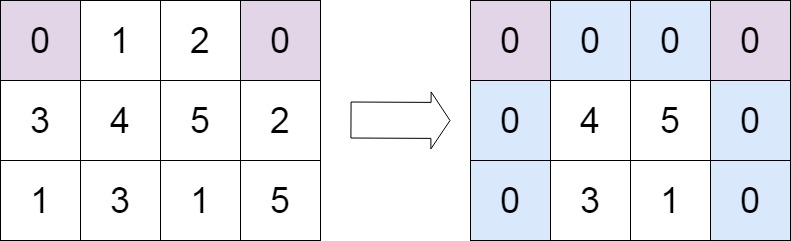
输入：matrix = $\[0,1,2,0$ , $3,4,5,2$ , $1,3,1,5$ ]

输出： $\[0,0,0,0$ , $0,4,5,0$ , $0,3,1,0$ ]

（来源：Leecode）

第一步：拆解问题的本质

我们要解决的"物理事实"是什么？

输入：一个的数值网格。
规则：如果某个点是 0，那么整个第行和第列都要变成 0。
约束：必须是原地（In-place） 。这意味着我们不能简单地通过复制一个完整的矩阵来解决问题（那会消耗的空间）。

核心矛盾：

如果我们直接遍历并修改矩阵，我们会污染数据。

比如：原本是 1，但因为它所在的第 0 行有另一个 0，它被改成了 0。
当我们随后遍历到时，我们会误以为它原本就是 0，从而错误地把第 0 列也清零。

推导出的基础真理：

我们需要一种方式来记录哪些行、哪些列需要清零，且这种记录不能干扰我们对"原始 0"的判断。

第二步：寻找存储空间的"最小化"

既然需要记录，记录在哪？

方案 A（直觉推导） ：创建一个的布尔矩阵记录 0 的位置。
- 评价：违背了原地算法的要求，空间复杂度太高。
方案 B（进一步压缩） ：我真的需要记录每一个点吗？不需要。我只需要知道"第行是否要清零"和"第列是否要清零"。
- 物理事实 ：我们需要个标记位（行）和个标记位（列）。
- 空间复杂度 ：。

第一性原理的终极拷问：

如果没有额外的空间呢？既然矩阵本身就在内存里，我们能不能借用矩阵内部的空间来做标记？

第三步：利用矩阵自身作为账本

如果我们用矩阵的第一行 和第一列 来充当那的标记位：

如果，我们就把设为 0（代表第行要清零），把设为 0（代表第列要清零）。

发现新的边界问题：

第一行和第一列本身也是数据。如果它们自己作为"账本"，那它们原本是否包含 0 的信息就会被覆盖。

解决方案：先用两个变量记录"第一行原本是否有 0"和"第一列原本是否有 0"，然后再开始借用它们。

第四步：代码实现

让我们按照上述逻辑编写 C++ 代码：

1. 初始化标记

首先，我们要确定第一行和第一列是否本来就需要清零。

cpp 复制代码

bool row0_has_zero = false;
bool col0_has_zero = false;

// 检查第一列
for (int i = 0; i < m; i++) {
    if (matrix[i][0] == 0) col0_has_zero = true;
}
// 检查第一行
for (int j = 0; j < n; j++) {
    if (matrix[0][j] == 0) row0_has_zero = true;
}

2. 遍历剩余部分并打标

我们利用第一行和第一列来记录 0 的出现情况。

cpp 复制代码

for (int i = 1; i < m; i++) {
    for (int j = 1; j < n; j++) {
        if (matrix[i][j] == 0) {
            matrix[i][0] = 0; // 标记行
            matrix[0][j] = 0; // 标记列
        }
    }
}

3. 根据标记清零

根据我们刚才在第一行/列留下的"脚印"，把内部元素清零。

cpp 复制代码

for (int i = 1; i < m; i++) {
    for (int j = 1; j < n; j++) {
        if (matrix[i][0] == 0 || matrix[0][j] == 0) {
            matrix[i][j] = 0;
        }
    }
}

4. 最后处理"账本"本身

别忘了，我们第一步记录的 row0_has_zero 还没用呢。

cpp 复制代码

if (col0_has_zero) {
    for (int i = 0; i < m; i++) matrix[i][0] = 0;
}
if (row0_has_zero) {
    for (int j = 0; j < n; j++) matrix[0][j] = 0;
}

完整代码如下：

cpp 复制代码

void setZeroes(vector<vector<int>>& matrix) {
    int m = matrix.size();
    int n = matrix[0].size();
    bool row0 = false, col0 = false;

    for(int i=0; i<m; i++) if(matrix[i][0] == 0) col0 = true;
    for(int j=0; j<n; j++) if(matrix[0][j] == 0) row0 = true;

    for(int i=1; i<m; i++) {
        for(int j=1; j<n; j++) {
            if(matrix[i][j] == 0) {
                matrix[i][0] = 0;
                matrix[0][j] = 0;
            }
        }
    }

    for(int i=1; i<m; i++) {
        for(int j=1; j<n; j++) {
            if(matrix[i][0] == 0 || matrix[0][j] == 0) matrix[i][j] = 0;
        }
    }

    if(col0) for(int i=0; i<m; i++) matrix[i][0] = 0;
    if(row0) for(int j=0; j<n; j++) matrix[0][j] = 0;
}

通过第一性原理，我们将问题的复杂度从降到了的额外空间。