Leetcode会员尊享面试100题：255.验证二叉搜索树的前序遍历序列

给定一个 无重复元素 的整数数组 preorder ， 如果它是以二叉搜索树的先序遍历排列 ，返回 true 。

示例 1：

复制代码

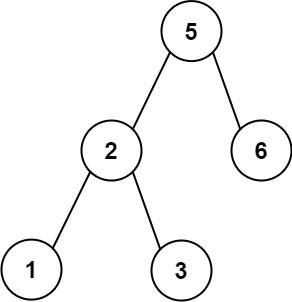
输入: preorder = [5,2,1,3,6]
输出: true

示例 2：

复制代码

输入: preorder = [5,2,6,1,3]
输出: false

提示:

1 <= preorder.length <= 104
1 <= preorder[i] <= 104
preorder 中 无重复元素

**进阶：**您能否使用恒定的空间复杂度来完成此题？

直接上代码，不懂请留言或私信

java 复制代码

class Solution {
    public boolean verifyPreorder(int[] preorder) {
        if(preorder.length == 1) {
            return true;
        }
        Info info = getInfo(preorder, 0, preorder.length - 1);
        return info.isBST;
    }
    /**当前树的范围是start～end，计算这棵树的Info信息 */
    public Info getInfo(int[] preorder, int start, int end) {
        if(start == end) {
            /**根据二叉搜索树的定义，如果只有一个节点就是 */
            return new Info(preorder[start], preorder[start], true);
        }
        /**拿到root的值 */
        int rootVal = preorder[start];
        /**现在我们还没有遍历不知道左右子树的情况，就以自己考虑设置minValue、maxValue还有isBST */
        int minValue = rootVal;
        int maxValue = rootVal;
        boolean isBST = true;
        /**这种情况只有右子树 */
        if(preorder[start + 1] > preorder[start]) {
            /**左子树为空，我们不用做任何关于左子树的比较*/
            Info info = getInfo(preorder, start + 1, end);
            /**统一写法*/
            minValue = Math.min(info.minValue, rootVal);
            maxValue = Math.max(rootVal, info.maxValue);
            isBST = info.isBST && rootVal < info.minValue;
            return new Info(minValue, maxValue, isBST);
        } else {
            /**有左子树，找一下左子树的终点的下一个位置*/
            int leftEndPost = searchFirstG(preorder, start + 1, end, rootVal);
            if(leftEndPost == -1) {
                /**只有左子树，剩下所有都是左子树的信息*/
                Info info = getInfo(preorder, start + 1, end);
                minValue = Math.min(info.minValue, rootVal);
                maxValue = Math.max(rootVal, info.maxValue);
                isBST = info.isBST && rootVal > info.maxValue;
                return new Info(minValue, maxValue, isBST);
            } else {
                /**左右子树都有，需要获取两颗子树的信息，左子树丛start+1~leftEndPost-1,右子树从leftEndPost～end */
                Info leftInfo = getInfo(preorder, start + 1, leftEndPost - 1);
                Info rightInfo = getInfo(preorder, leftEndPost, end);
                minValue = Math.min(leftInfo.minValue, Math.min(rootVal, rightInfo.minValue));
                maxValue = Math.min(leftInfo.maxValue, Math.min(rootVal, rightInfo.maxValue));
                /**这里需要左右子树都判断，左子树最大值必须比rootVal小，右子树最小值必须比rootVal大 */
                isBST = leftInfo.isBST && rightInfo.isBST && leftInfo.maxValue < rootVal && rightInfo.minValue > rootVal;
                return new Info(minValue, maxValue, isBST);
            }
        }
    }
    /**获取第一个大于root值的元素，使用二分查找*/
    public int searchFirstG(int[] arr, int start, int end, int rootVal) {
        if(start > end) {
            return -1;
        }
        /**先定义为-1，如果没有查找到最后就是-1，如果查找到了大雨rootVal的就更新成满足条件的最小的 */
        int index = -1;
        while(start <= end) {
            int mid = start + (end - start)/2;
            /**根据题意，无重复元素，所以这里直接判断大于就行，一般的二分是需要写>= */
            if(arr[mid] > rootVal) {
                /**找到了一个大于等于的，但是这未必是最终的答案，需要继续往小了找 */
                index = mid;
                end = mid - 1;
            } else {
                /**范围错了，如果有这个值肯定在前面 */
                start = mid + 1;
            }
        }
        return index;
    }
}

/**根据二叉搜索树的特性：根节点比它左子树的任何节点都大
比它右子树的任何节点都小，并且左右子树都是二叉搜索树，所以我们需要左右子树的以下信息：最大值、最小值、是否为二叉搜索树*/
class Info{
    int minValue;
    int maxValue;
    boolean isBST;
    public Info(int minValue, int maxValue, boolean isBST) {
        this.minValue = minValue;
        this.maxValue = maxValue;
        this.isBST = isBST;
    }
}

运行结果：