最近忙着考驾照...v20min又被喊去吃饭了...慢慢补题吧
D 构造 位运算

题意:计算前缀与的码重(1的个数)
从二进制角度想,一旦 p i p_i pi一位上出现0,之后这一位都没有贡献了,所以要让 p i p_i pi越晚出现0越好
容易想到把1对齐,固定 n o w now now个位上一直有1 ( n o w = n , n − 1 , . . . , 1 , 0 ) (now=n,n-1,...,1,0) (now=n,n−1,...,1,0),其他位上随便枚举
比如n=5时
11111
01111
00111
10111
00011
01011
10011
11011
00001
...
我是选的低几位的固定为1
注意这样枚举,枚举位要和固定位隔一个0
cpp
void solve(){
int n;cin>>n;
vector<int>a,vis((1<<n),0);
int now=n;
/* 错了
while(now){
a.push_back(now);
vis[now]=1;
now>>=1;
}
forr(i,1,(1<<(n-1))-1){
if(vis[(i<<1)+1])continue;
a.push_back((i<<1)+1);
vis[(i<<1)+1]=1;
}
forr(i,0,(1<<(n-1))-1){
a.push_back((i<<1));
}*/
while (now>-1)
{
int base=max(0,(1<<now)-1),lst=(1<<max(0ll,(n-now-1)))-1;
a.push_back(base);
forr(i,1,lst){
a.push_back((i<<(now+1))+base);
}
now--;
}
for(auto x:a)cout<<x<<' ';
cout<<endl;
}E 分类讨论 构造

感觉是很复杂的分类讨论
参考@znzryb dalao题解
关键思路:本题的关键在于"每个选区至少 p i p_i pi张票"。即使我们满足了所有下界,剩余的票也必须分配到某些选区,且不能改变原有的胜负关系。
思路流程:将每个位置胜负关系固定,并"对半分"让票数使用最少→分类讨论剩下的票数情况,多的适当填充进去,少的抽出
- 填充:
- 向胜利(票数占多数)地方填充,多的更多
- 没有获胜的选区,发现偶数"对半分"有空隙可以填补
- 剩下的票用对方票抵消,维持胜负关系
- 抽出:
- 从失败选区抽出,少的更少。为了维持数目 ≥ p i \geq p_i ≥pi,需要对方票来补充。
- 抽出完成,剩下的票按填充规则继续填充进去
cpp
#define rno cout<<"NO"<<endl
#define ryes cout<<"YES"<<endl
void solve(){
int n,a,b;cin>>n>>a>>b;
string s;cin>>s;
vector<int>cnt(2,0);
for(auto c:s){
cnt[c-'0']++;
}
vector<int>p(n+1);
int ra=a,rb=b;//resta restb 最少分配后剩余的a,b
forr(i,1,n){
cin>>p[i];
int ca,cb;
//这种"对半分"的分配方式 是让多数的那一方用的最少
if(s[i-1]=='0'){
ca=p[i]/2+1;
cb=p[i]-ca;
}else{
cb=p[i]/2+1;
ca=p[i]-cb;
}
ra-=ca;
rb-=cb;
}
//填充
auto putin=[&]()->bool{
if(ra>=0&&rb>=0){ //ab两边都有剩余
if(cnt[0]&&cnt[1])return ryes,true; //ab都有多数位置 把剩余的往多数里塞
else if(cnt[0]){ //只有a多数
///如p[i]=2x c1=p[i]/2+1=x+1 c2=p[i]-c1=x-1 c2-c1=2 b有1个的空隙能塞
int del=0; //统计还能塞的空隙
forr(i,1,n){
int ca=p[i]/2+1,cb=p[i]-ca;
del+=max(0ll,ca-cb-1);
}
// rb填满空隙后 剩下的和ra一换一 保持a多数不变
if(ra>=rb-del)return ryes,true;
}else if(cnt[1]){ //只有b多数 和上面对称
int del=0;
forr(i,1,n){
int cb=p[i]/2+1,ca=p[i]-cb;
del+=max(0ll,cb-ca-1);
}
if(rb>=ra-del)return ryes,true;
}
}
return false;
};
if(ra<0&&rb<0)return rno,void();
else if(ra>=0&&rb>=0){ //ab两边都有剩下的票 填充
if(putin())return;
}else{ //有一边剩下的是负数 就是过量用了 需要抽出
if(ra>=abs(rb)){ //b被过量用了 并且a能把b补上
forr(i,1,n){
if(s[i-1]=='0'){ //b多数的已经是最少了 只能从b少数抽回,b少数的地方更少,并用多数的a补上
int ca=p[i]/2+1,cb=p[i]-ca;
int pullout=min({cb,ra,abs(rb)});
ra-=pullout,rb+=pullout;
}
}
//补完了 此时ra>=0,rb=0 分配剩下多出来的
if(putin())return;
}
if(rb>=abs(ra)){ //b把a补上
forr(i,1,n){
if(s[i-1]=='1'){
int cb=p[i]/2+1,ca=p[i]-cb;
int pullout=min({ca,rb,abs(ra)});
ra+=pullout,rb-=pullout;
}
}
//补完了
if(putin())return;
}
}
rno;
}F 二分图 构造
题好长,读了好长时间:
- agent先把所给二分图中节点涂上rgb三种颜色
- 玩家b再根据相邻节点颜色从任意一点走到节点1,b不知道整个图的情况和所在节点的颜色,需要仅通过邻居颜色推导方向
往顶点1的方向走,每次不断缩小与1的距离,核心思路就是把颜色和距离变化绑定
偷个懒,直接引用dalao题解的清晰讲解
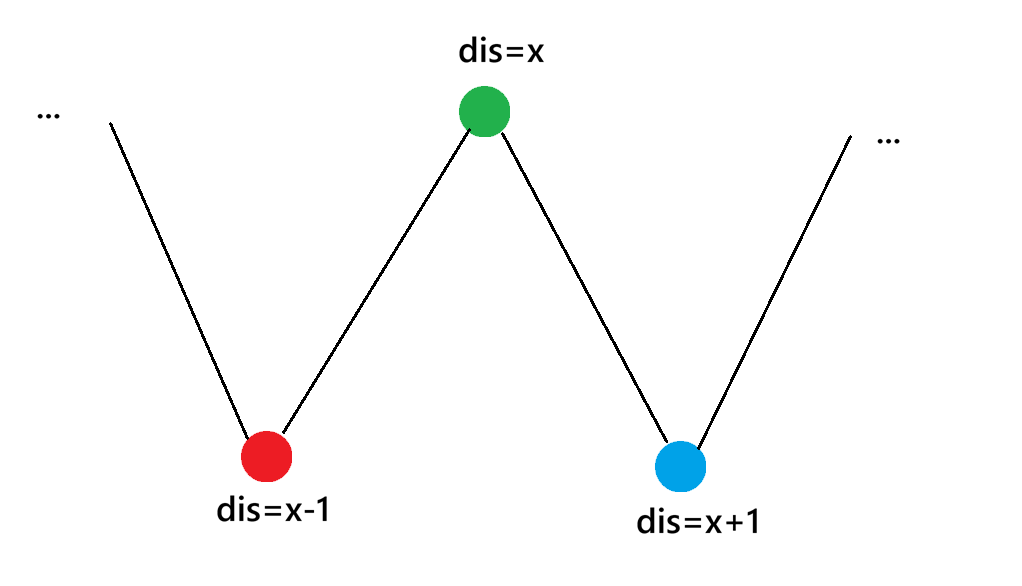
结论:二分图的每条边相连的两点,到节点1的距离一定相差1,奇偶性不同。于是需要用两种颜色区分是"靠近"(-1)还是"远离"(+1)
一共3种颜色,自然会想到距离模3染色
d i s % 3 = 0 → r = 1 → g = 2 → b dis\%3 =0\rightarrow r\\ =1\rightarrow g\\=2\rightarrow b dis%3=0→r=1→g=2→b
靠近: ( d i s − 1 ) % 3 (dis-1)\%3 (dis−1)%3是"rgb"顺序中前一位颜色
远离: ( d i s + 1 ) % 3 (dis+1)\%3 (dis+1)%3是"rgb"顺序中后一位颜色
每个顶点的邻居颜色组合,要么是两种(靠近 + 远离),要么是一种(全靠近或全远离),且两种颜色的组合必然 "缺一种颜色"------ 而缺失的颜色,恰好是自身的颜色。
cpp
string clr="rgb";
void solve1(){
int n,m;cin>>n>>m;
vector<int>g[n+5];
forr(i,1,m){
int a,b;cin>>a>>b;
g[a].push_back(b);
g[b].push_back(a);
}
// dij求各点最短距离
vector<int>dis(n+1,inf),vis(n+1,0);
auto dij=[&]()->void{
dis[1]=0;
priority_queue<pii>q;
q.push({0,1});
while (q.size())
{
auto [t,now]=q.top();
q.pop();
if(vis[now])continue;
vis[now]=1;
for(auto x:g[now]){
if(dis[x]>dis[now]+1){
dis[x]=dis[now]+1;
q.push({-dis[x],x});//大根堆
}
}
}
};
dij();
forr(i,1,n){
cout<<clr[dis[i]%3];
}cout<<endl;
}
void solve2(){
int q;cin>>q;
while(q--){
int d;cin>>d;
string ds;cin>>ds;int ls=ds.size();
map<char,int>id;
forr(i,0,ls-1)id[ds[i]]=i+1;
if(id.size()==1){
cout<<1<<endl;
}else{
forr(i,0,2){
if(!id[clr[i]]){
cout<<id[clr[(i+3-1)%3]]<<endl;
}
}
}
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int _ = 1;
string s;cin>>s;
cin >> _;
while (_--)
{
if(s[0]=='f')solve1();
else solve2();
}
return 0;
}