第八章 - 贪心法

UVA120 煎饼 Stacks of Flapjacks

思路：

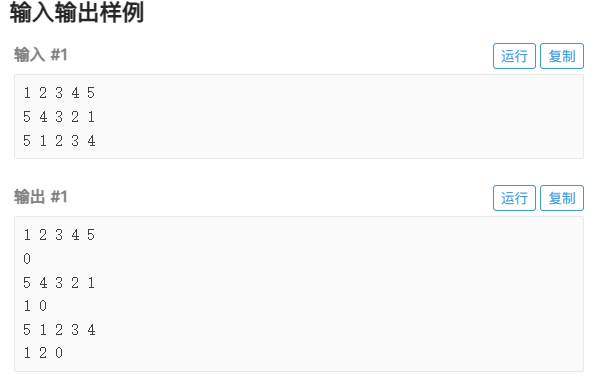
要求通过翻转 1~刀插入位置的所有数，使煎饼的半径做到从小到大排，那么思路就很清晰了：先找到最大的数，翻转把它扔到最后，再找到第二大的数，也想办法翻转，扔到倒数第二个；

这里会出现一个问题：

就是这个我们要找的当前最大数是否在第1位，如果是，则直接翻转最后一个煎饼，把这个半径最大的煎饼扔到后面去；如果不是呢？就把它翻转到第一位，再扔到后面去；

简单来说，找到起始位置 i 和结束位置 p，然后从两边开始交换。

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
int main() {
    string line;
    while (getline(cin, line)) {
        vector<int> a, b;
        stringstream ss(line);  // 使用字符串流解析数字
        int p;
        while (ss >> p) {a.push_back(p);b.push_back(p);}
        sort(b.begin(), b.end());//升序排序作为模版
        
        p = b.size();//从最后一个开始处理  /* cout << a[p-1] << endl; */
        while(p > 0){
            bool cg = true;
            for (size_t t = 0; t < a.size(); t++){if(a[t] != b[t]) cg = false;} 
            if(cg){cout << '0' << endl;break;}
            
            int i = 0;
            for (size_t t = 0; t < p; t++){
                if(a[t] == b[p-1]) i = t;
            }    //将第 p 个数的数组下标给 i 
            if(i != p-1){
                if(i != 0){//第 p 个数不在最上面，翻转到最上面
                    reverse(a.begin(),a.begin() + i + 1);
                    cout << b.size() - i << ' ';
                }
                
                //将第 p 个数翻转到最下层（比p直径大的上一层）
                reverse(a.begin(),a.begin() + p);
                cout << b.size() - p + 1 << ' ';
            }
            p--;
        }
    }
    return 0;
}

UVA11134 传说中的车 Fabled Rooks

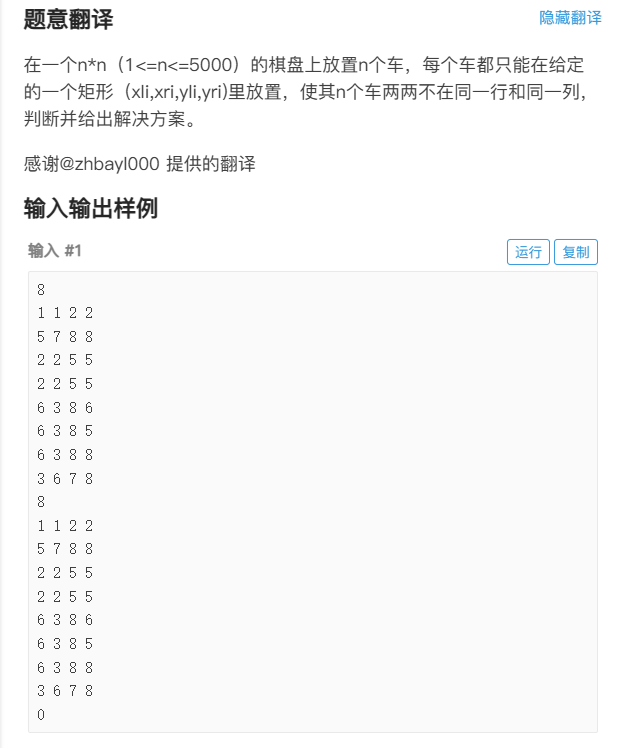
首先，我们发现其实x轴与y轴是互不相关的，可以独立求解。于是我们把x轴与y轴分开求解。于是问题就变成了：在[1,n]的区间中，有一些区间，在每一个区间中选一个点，使最终恰好覆盖[1,n]中的这n个点。

开始时，我想的是以l作为第一关键字，r作为第二关键字进行排序。然后从左往右扫。然而这样显然是不成立的，[1,3],[1,3],[2,2]这组数据就会被卡掉。

在用贪心法解决问题时，我们可以考虑：如果要选择几种状态，一种决策的"后路"覆盖了所有其他决策的"后路"，那我们不应当选择这种决策。（可能我语文不怎么好，那就用这道题解释一下吧。）

试想一下，如果我们要求从前往后做出抉择，且有两段区间都可以选择，那我们应该选择哪一段？显然是r值小的哪一段。应为对于后面的点，r值小的可以覆盖的点r值大的也可以覆盖，而r值大的可覆盖的点r值小的可能无法覆盖。这样，我们可以认为r值大的"后路"覆盖了r值小的的所有后路，于是我们应该选r值小的。于是我们就不难想到方法：以r（后路）作为关键字排序（r相同的可以随意排），然后对于每一个序列，从l到r扫描。如果是该点没有被选择过，那就选择该点。

问题分解：将二维棋盘问题分解为两个独立的一维问题

贪心策略 ：按右端点从小到大排序，然后每个区间选择最小的可用位置

正确性：右端点小的区间选择余地小，应该优先安排

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    while (cin >> n && n) {
        struct Node { int l, r, id; };
        vector<Node> rows(n), cols(n);
        
        // 读取
        for (int i = 0; i < n; i++) {
            int xl, yl, xr, yr;
            cin >> xl >> yl >> xr >> yr;
            rows[i] = {xl, xr, i};
            cols[i] = {yl, yr, i};
        }
        
        // 按右端点排序
        auto cmp = [](const Node& a, const Node& b) {
            return a.r == b.r ? a.l < b.l : a.r < b.r;
        };
        sort(rows.begin(), rows.end(), cmp);
        sort(cols.begin(), cols.end(), cmp);
        
        vector<int> ans_x(n), ans_y(n);
        vector<bool> used_x(n + 1, false), used_y(n + 1, false);
        bool ok = true;
        
        // 处理x坐标
        for (auto& node : rows) {
            int pos = node.l;
            while (pos <= node.r && used_x[pos]) pos++;
            if (pos > node.r) { ok = false; break; }
            used_x[pos] = true;
            ans_x[node.id] = pos;
        }
        
        // 处理y坐标
        if (ok) {
            for (auto& node : cols) {
                int pos = node.l;
                while (pos <= node.r && used_y[pos]) pos++;
                if (pos > node.r) { ok = false; break; }
                used_y[pos] = true;
                ans_y[node.id] = pos;
            }
        }
        
        // 输出
        if (ok) {
            for (int i = 0; i < n; i++) 
                cout << ans_x[i] << " " << ans_y[i] << endl;
        } else {
            cout << "IMPOSSIBLE" << endl;
        }
    }
    return 0;
}