【线性 VS 逻辑回归：一篇讲透两种核心回归模型】

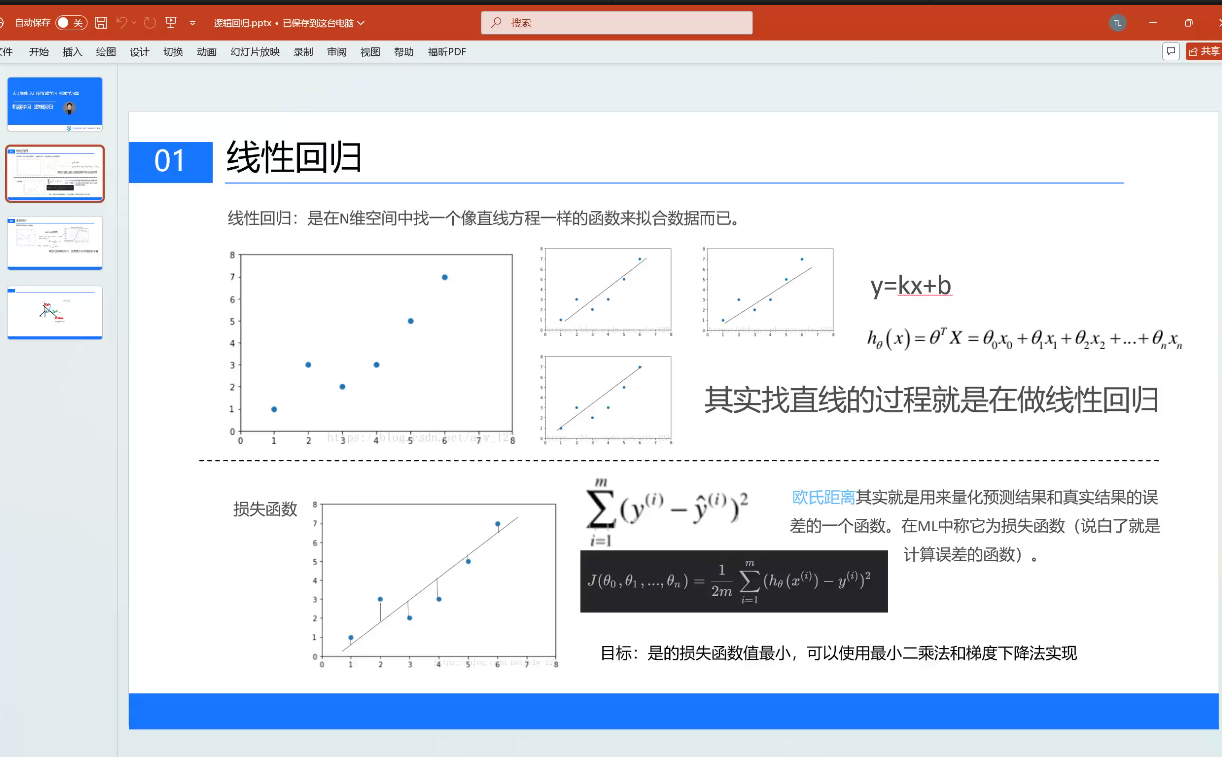
线性回归

在N维空间中找到一个像直线方程一样的函数来拟合数据

基于多元线性回归的数据建模与分析，针对体重、年龄与血压收缩压之间的关系进行建模和预测。

import pandas as pd
from sklearn.linear_model import LinearRegression
#导入数据，指定编码为 'gbk' 以兼容中文，engine='python' 处理特殊字符
# open(encoding=)
data = pd.read_csv("多元线性回归.csv",encoding='gbk',engine='python')
#打印相关系数矩阵，查看特征间的相关性
corr = data[["体重","年龄","血压收缩"]].corr()
print(corr)
#第二步，估计模型参数，建立回归模型
lr_model = LinearRegression()#初始化模型
x = data[['体重','年龄']]#两个特征：体重和年龄
y = data[['血压收缩']]#目标变量
lr_model.fit(x,y)#训练模型，拟合数据寻找最佳参数
#第四步，对回归模型进行检验
'''score:调整R方，判断自变量对因变量的解释程度R方越接近于1，自变量对因变量的解释就越好
F检验:方程整体显著性检验
T检验:方程系数显著性检验
score给的是R方
'''
score =lr_model.score(x,y)#sklearn statsmodes(数理统计这个专业)
print(lr_model.predict(x))
#第五步，利用回归模型进行预测
print(lr_model.predict([[80,60]]))
print(lr_model.predict([[70,30],[70,20]]))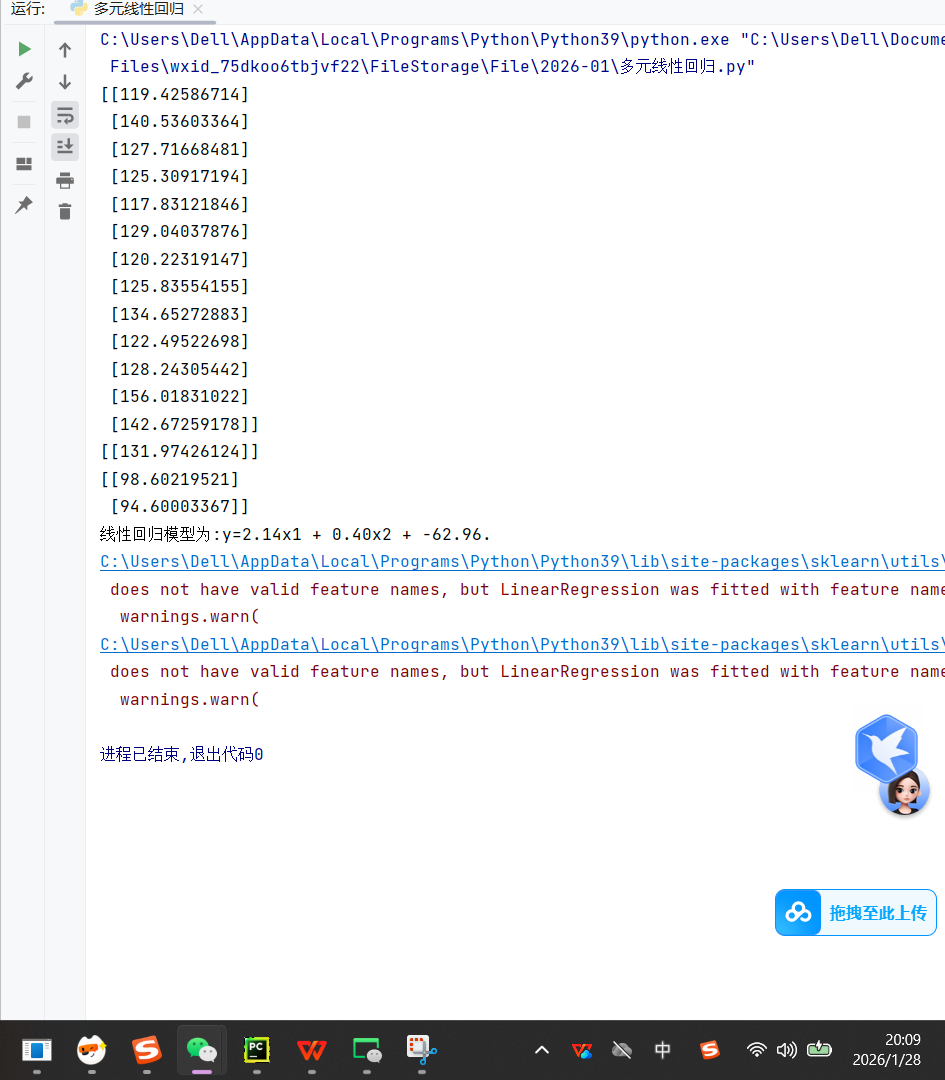

统计学概念：

• R² (决定系数)：衡量模型对因变量变化的解释程度。范围通常在 0 到 1 之间，越接近 1 说明拟合效果越好。
• F 检验：用于检验回归方程整体的显著性，即所有自变量的系数是否同时为零。
• T 检验：用于检验单个回归系数的显著性，即某个自变量是否对因变量有显著影响

LinearRegression 类详解

class sklearn.linear_model.LinearRegression (fit_intercept=True , normalize=False , copy_X=True , n_jobs=None )

1.参数：

fit_intercept: 布尔值，默认为True。决定是否计算模型的截距。若数据已中心化，可设置为False。是否有截据，如果没有则直线过原点。

**normalize:**布尔值，默认为False。是否对数据进行归一化处理。该参数在fit_intercept=False时无效。

copy_X ： 是否对X复制，如果选择false，则直接对原数据进行覆盖而非修改原数据。（即经过中心化，标准化后，是否把新数据覆盖到原数据上）

n_jobs： 计算时设置的任务个数(number of jobs)。如果选择-1则代表使用所有的CPU。这一参数的对于目标个数>1（n_targets>1）且足够大规模的问题有加速作用。

2.属性：

C oef _:数组

对于线性回归问题计算得到的feature的系数。如果输入的是多目标问题，则返回一个二维数组(n_targets, n_features)；如果是单目标问题，返回一个一维数组 (n_features,)。

intercept_ ：浮点数

线性模型中的独立项。

3.方法 ：

**fit(X, y[, n_jobs]) ：fit(X, y)，**X训练集, y标签

对训练集X, y进行训练。

predict(X)：X数据集，对输入数据 X 进行预测

使用训练得到的估计器对输入为X的集合进行预测（X可以是测试集，也可以是需要预测的数据）。

**score(X, y[,]sample_weight)：score(X, y)，**X, y测试集

返回 R² 决定系数。值越接近 1，模型解释能力越强。

逻辑回归

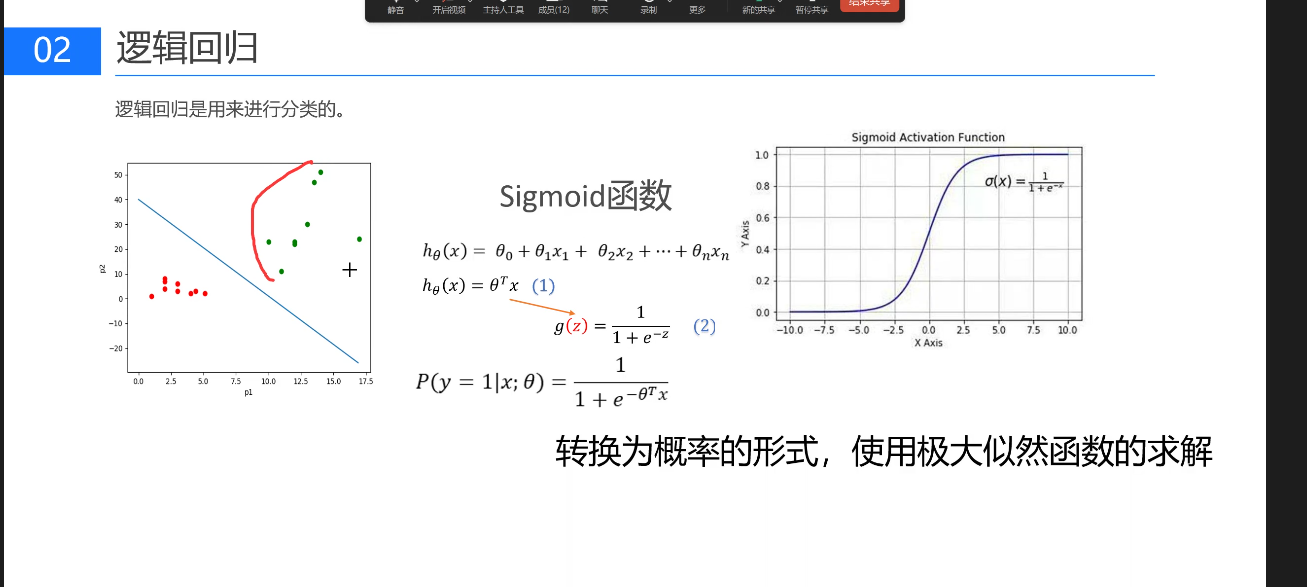
逻辑回归是改进线性回归使其适用于分类任务的方法。它基于线性回归原理，通过构建一条线将数据点分隔，并使用sigmoid函数将结果映射到0和1之间作为概率。目标是找到使所有点概率最大的线，从而正确分类数据。核心在于建立模型，将输入数据映射到sigmoid曲线，求解使概率最大的参数。

1.构建线性模型：和线性回归一致，计算线性得分

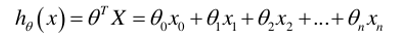
2.Sigmoid 函数映射：将线性得分 z 代入 Sigmoid 函数，转换为 0-1 之间的概率值。

Sigmoid 函数数学表达式：

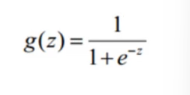
它是一条 "S" 形曲线，自变量 z 为任意实数，输出值严格落在 (0,1) 区间，可理解为 "样本属于正类的概率"；

3.分类判定： 以 0.5 为阈值，概率 > 0.5 判定为正类，<0.5 判定为负类（阈值可根据业务调整，如风控场景可降低阈值提高召回率）。

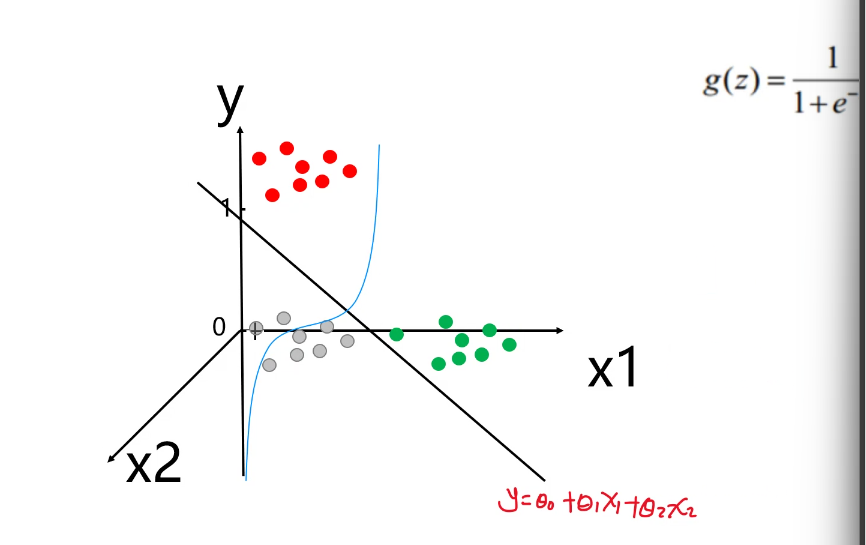
以银行贷款异常检测为案例，实现从数据读取到模型评估的全闭环，核心模块如下：

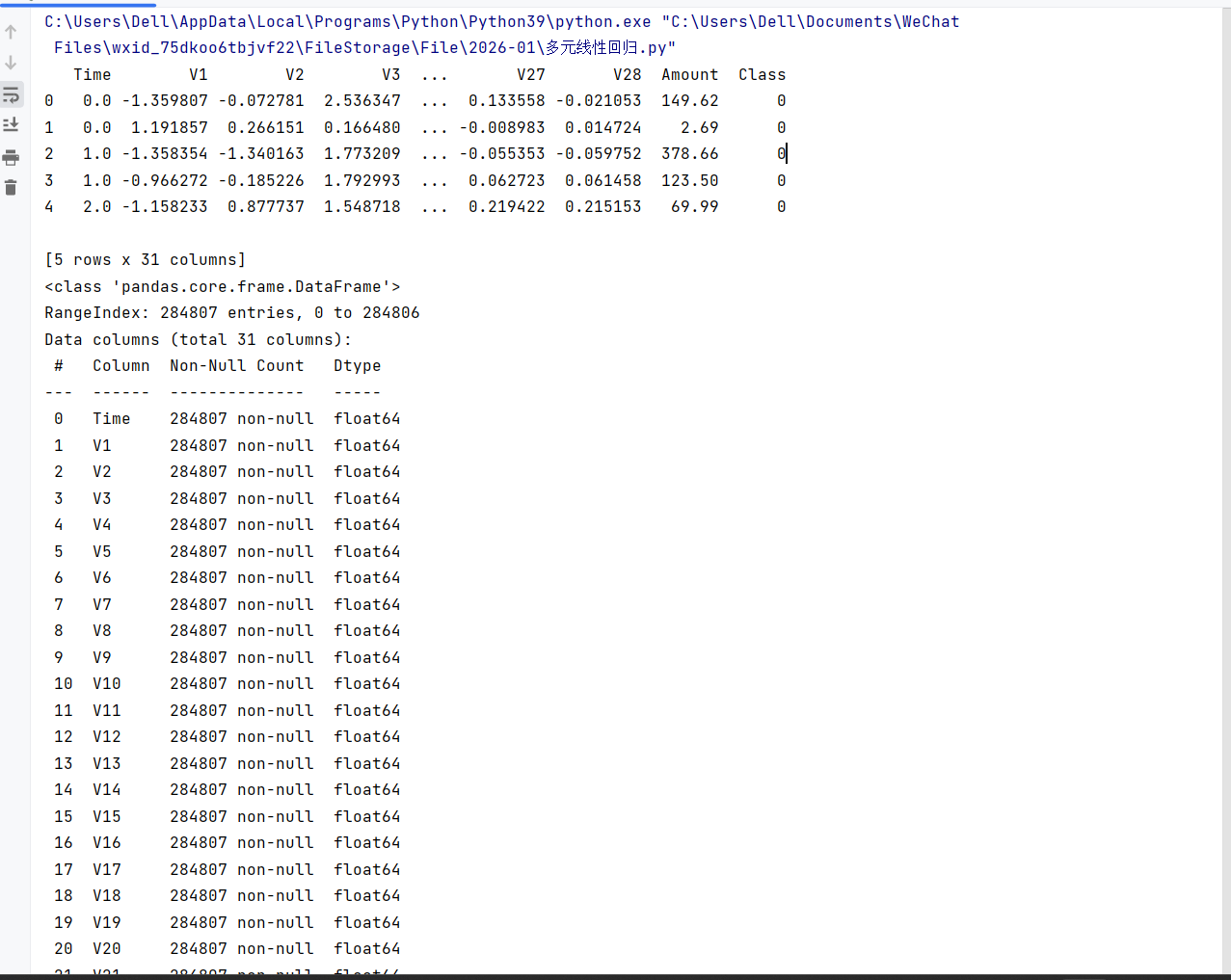
1.导入环境，读取数据集信息：使用 creditcard.csv 数据集，含 Time（时间）、Amount（金额）、Class（标签，0 为正常、1 为异常）及 V1-V28 共 31 列特征，数据已脱敏处理。

可视化工具：matplotlib 绘制正负样本柱状图，设置中文显示（font.sans-serif='Microsoft YaHei'），直观呈现类别分布差异。

import pandas as pd
import matplotlib.pyplot as plt
from pylab import mpl
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report

# 中文显示配置
mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']
mpl.rcParams['axes.unicode_minus'] = False

# 读取数据（处理编码问题）
data = pd.read_csv(r"./creditcard.csv", engine="python")
print(data.head())  # 查看数据前5行
print(data.info())  # 查看数据基本信息

2.数据预处理，预处理步骤：删除无关列（Time）、对 Amount 特征做 Z 标准化，消除量纲）、通过可视化查看样本分布（正负样本极度不均衡）。

# 1. Z标准化处理Amount特征
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])

# 2. 删除无关列（Time列）
data = data.drop(['Time'], axis=1)

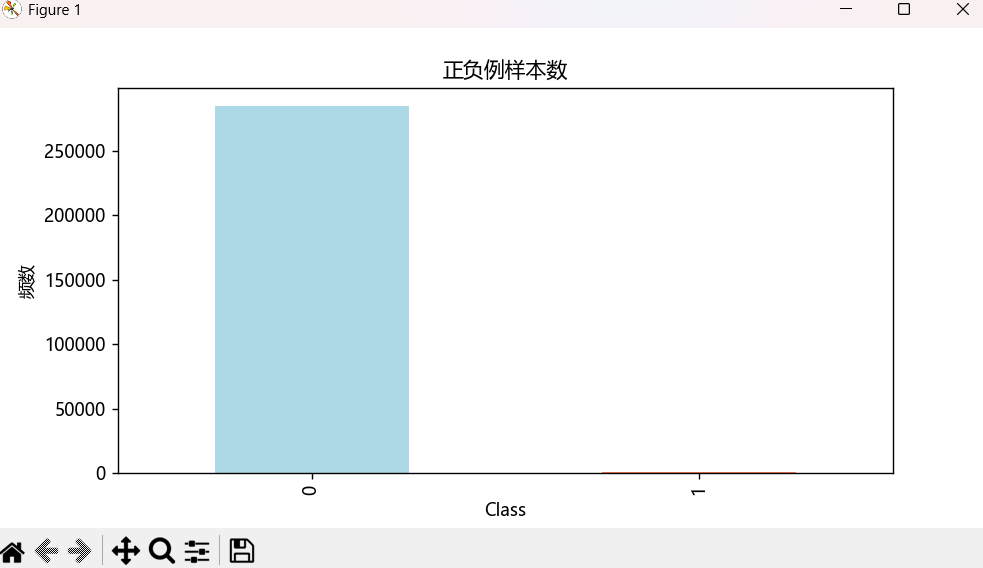
# 3. 统计并可视化正负样本分布
labels_count = pd.value_counts(data["Class"])
print("正负样本数量：\n", labels_count)
plt.figure(figsize=(8, 4))
plt.title("正负例样本数")
plt.xlabel("类别（0=正常，1=异常）")
plt.ylabel("频数")
labels_count.plot(kind='bar', color=['lightblue', 'coral'])
plt.show()

3.数据集划分，用 train_test_split 拆分训练集与测试集，test_size=0.3（测试集占比），random_state=1000（固定随机种子确保可复现）。然后进行模型训练

# 划分特征集（X）与标签集（y）
X_whole = data.drop('Class', axis=1)
y_whole = data['Class']

# 拆分训练集与测试集
X_train_w, X_test_w, y_train_w, y_test_w = train_test_split(
    X_whole, y_whole, test_size=0.3, random_state=1000
)

# 初始化逻辑回归模型（配置关键参数）
lr = LogisticRegression(
    penalty='l2',  # L2正则化
    C=0.01,        # 较强正则化强度
    solver='liblinear',  # 适配二分类的求解器
    max_iter=100   # 迭代次数
)

# 训练模型
lr.fit(X_train_w, y_train_w)

4.模型预测与评估（评估指标：准确率（score 函数）、F1-score、混淆矩阵（适配样本不均衡场景）。）

# 模型预测
test_predicted = lr.predict(X_test_w)

# 1. 输出准确率
accuracy = lr.score(X_test_w, y_test_w)
print(f"模型准确率：{accuracy:.4f}")

# 2. 输出详细分类报告（含F1-score等）
print("\n分类报告：")
print(classification_report(y_test_w, test_predicted))

运行结果：

LogisticRegression API 参数详解

penalty（正则化类型）正则化类型（'l1' 或 'l2'），L1 适合特征选择，L2 适合防止过拟合；

C（正则化强度）

正则化强度倒数，值越小正则化越强（默认 1.0）

solver（优化算法）求解器选择（'liblinear'适配小数据集，'lbfgs'/'sag'适配大数据集）

max_iter （最大迭代次数）

优化算法的迭代上限，默认 100。若未收敛会触发警告。

class_weight（类别权重）

处理样本不均衡（'balanced' 自动调整权重，或手动传入字典如 {'0':1, '1':10}）；

random_state（随机种子）

控制随机性（solver 为'sag'/'liblinear' 时生效）

fit_intercept （是否拟合截距）

布尔值，默认 True。若数据已中心化可设为 False。

intercept_scaling （截距缩放）

仅当 solver='liblinear' 且 penalty='l2' 时生效，通常无需调整。

召回率：

模型评估核心指标（基于混淆矩阵）

• 混淆矩阵核心定义：

◦ TP（True Positive）：真实值为 1、预测值为 1（真阳性）；

◦ FN（False Negative）：真实值为 1、预测值为 0（假阴性）；

◦ FP（False Positive）：真实值为 0、预测值为 1（假阳性）；

◦ TN（True Negative）：真实值为 0、预测值为 0（真阴性）。

• 核心评估指标公式：

◦ 准确率（Accuracy）：(TP+TN)/(TP+TN+FP+FN)，反映模型整体预测正确的比例；

◦ 精确率（Precision）：TP/(TP+FP)，反映预测为正类的样本中实际为正类的比例；

◦ 召回率（Recall）：TP/(TP+FN)，反映真实为正类的样本中被正确预测的比例（对异常检测等场景关键）；

◦ F1-score：2×(Precision×Recall)/(Precision+Recall)，综合精确率和召回率，平衡两者冲突

评价方式：

1.分类：AUC，Score

2.回归：R的平方