【机器学习】标准化流模型（NF）

与 VAE 的近似概率推断 、GAN 的无显式概率密度 、扩散模型的逐步去噪采样 不同，标准化流的核心思想是：从简单的已知基分布（如高斯分布）出发，通过一系列 可逆、雅可比行列式易计算的光滑变换，将其映射为与真实数据分布高度拟合的复杂目标分布 。同时，利用概率变量替换公式，可精确计算目标分布的概率密度，这是其区别于其他生成模型的核心优势。

标准化流在密度估计、可控生成、变分推断、强化学习 等领域应用广泛，尤其适合对概率密度计算精度有要求 的场景（如异常检测、分子生成、策略建模）。本文将从核心定位与优势 、数学基础（必懂） 、核心原理与基本框架 、关键设计原则 、经典基础变换与主流模型 、训练方法 、优缺点 、应用场景 八个维度详细讲解，以及Python代码完整实现，兼顾理论严谨性和直观理解，同时对比其他生成模型突出其特性。

二、核心定位与核心优势

1. 核心定位

标准化流是基于可逆变换的精确概率生成模型 ，属于显式密度模型（Explicit Density Model），核心目标有两个：

密度估计：精确计算任意样本在真实数据分布中的概率密度p(x)；
生成建模：从简单基分布采样，经可逆变换生成符合真实数据分布的样本x。

其所有设计都围绕 **"可逆变换"和"雅可比行列式易计算"** 展开，这是实现上述两个目标的前提。

2. 与其他主流生成模型的核心对比

标准化流的优势和特点，在与 GAN、VAE、扩散模型的对比中体现得最为明显（下表为核心维度对比，聚焦生成模型的核心诉求）：

模型类型	概率密度特性	采样特性	训练稳定性	核心优势	核心缺陷
标准化流	精确计算（无近似）	直接采样（部分模型高效）	高（似然优化）	精确密度估计、无模式崩溃、可控生成	高维数据建模难度大、表达能力受限于变换
VAE	近似计算（变分下界）	随机采样（存在模糊）	中	训练简单、结合变分推断	样本模糊、密度估计不精确
GAN	无显式密度	直接采样（高效）	低（模式崩溃、梯度消失）	样本质量高、生成效率高	无密度估计、训练不稳定
扩散模型	近似计算（逐步估计）	逐步采样（速度慢）	高	样本质量极高、适合高维图像	采样效率低、无精确密度估计

3. 标准化流的核心优势

精确的概率密度估计 ：通过变量替换公式可直接计算样本的对数似然，是所有生成模型中唯一能实现精确密度估计的类型，适合异常检测、概率预测等对密度精度有要求的场景；
训练稳定 ：训练目标是最大化数据的对数似然（MLE），属于有监督的优化问题，无 GAN 的模式崩溃、梯度消失问题，也无 VAE 的变分下界近似偏差；
可逆的生成与推断 ：变换的可逆性让 "基分布→目标分布（生成）" 和 "目标分布→基分布（推断）" 成为双向过程，可实现可控生成（如基于基分布的隐变量调整生成样本的特征）；
无模式崩溃：对数似然的优化目标会让模型尽可能拟合所有数据的分布，不会出现 GAN 中只拟合部分数据模式的问题。

三、数学基础（必懂，核心公式）

标准化流的所有理论都基于概率论的变量替换公式 ，这是模型的 "数学基石"，同时依赖可逆变换 和雅可比行列式两个概念，先掌握这三个基础，后续原理会迎刃而解。

1. 一维变量替换公式（直观入门）

先从一维情况入手，理解核心逻辑，高维是一维的自然推广。

假设存在可逆的单调可微变换 y=f(x)，其逆变换为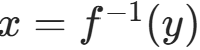；已知随机变量X的概率密度函数为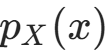，求随机变量Y=f(X)的概率密度函数。

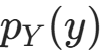根据概率的基本性质（概率质量守恒），X落在区间 $x,x+dx$ 的概率等于Y落在区间 $y,y+dy$ 的概率，即：

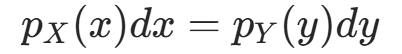
变形后得到一维变量替换公式：

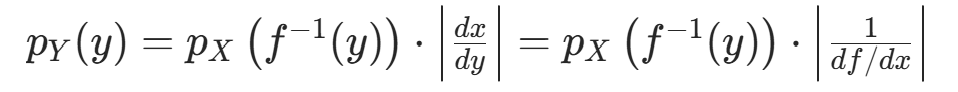
其中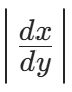是导数的绝对值，表示变换后的 "体积缩放因子"------ 变换会拉伸 / 压缩概率空间，导数绝对值用于修正这种缩放，保证概率密度的积分和为 1。

简单例子：设X∼N(0,1)（标准高斯），变换y=2x+1（可逆线性变换），逆变换x=(y−1)/2，导数dx/dy=1/2，则Y的密度为：

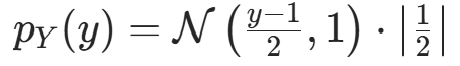
即Y∼N(1,4)，与线性变换的高斯分布性质一致，验证了公式的正确性。

2. 高维变量替换公式（模型核心）

标准化流处理的是高维数据（如图像、语音、特征向量），需要推广到高维情况，此时导数变为雅可比矩阵 ，导数的绝对值 变为雅可比行列式的绝对值。

（1）核心概念定义

设高维随机变量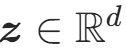（基分布样本），经可逆光滑变换 x=f(z)映射为高维随机变量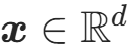（目标分布样本）；
逆变换为；
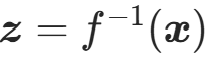雅可比矩阵 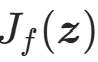：变换f在z处的雅可比矩阵是d×d的矩阵，第i行第j列的元素为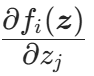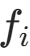（是f的第i个分量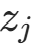，是z的第j个分量）；
雅可比行列式 ：记为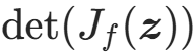，是方阵的行列式，仅方阵有行列式；
变换可逆的充要条件：雅可比矩阵非奇异 （）。

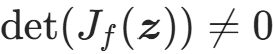（2）高维变量替换公式

根据概率质量守恒，高维情况下的概率密度变换公式为：

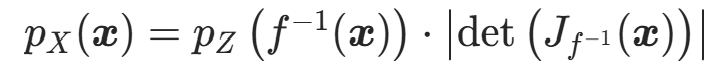
其中：

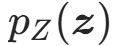：基分布的概率密度（已知、简单，如标准多元高斯N(0,I)）；
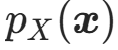：目标分布（真实数据分布）的概率密度，即标准化流要估计的密度；
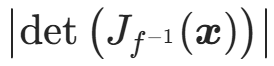：逆变换的雅可比行列式的绝对值，高维的 "体积缩放因子"。

（3）更实用的等价形式

利用逆矩阵的行列式性质 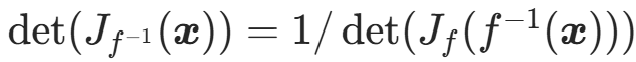：，公式可改写为：

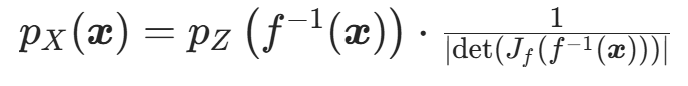
该形式更适合标准化流的计算，因为实际中常先计算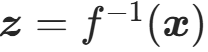，再计算正变换f在z处的雅可比行列式。

3. 对数似然形式（训练核心）

直接计算概率密度会出现数值下溢 （高维下密度值极小，连乘后趋近于 0），因此标准化流中通常使用对数似然形式，利用对数的单调性和积转和性质，将乘法变为加法，避免数值问题。

对高维变量替换公式取自然对数，得到：

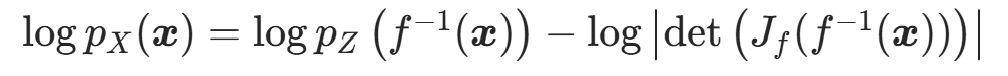
这是标准化流最核心的公式，模型的训练、密度估计、采样均围绕该公式展开，需牢记！

四、标准化流的核心原理与基本框架

基于上述数学基础，标准化流的核心原理可概括为 **"一次基分布定义 + 一系列可逆变换复合 + 两个核心操作（密度估计 / 采样）"**，整体框架简洁且逻辑严谨。

1. 核心定义

（1）基分布（Base Distribution）

选择简单、已知、易采样、密度易计算 的高维分布作为基分布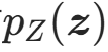，是标准化流的起点，最常用的是标准多元高斯分布：

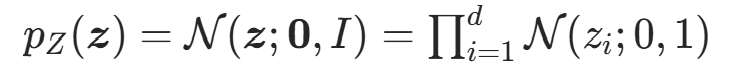
其采样可直接通过随机数生成器实现，对数密度计算为：

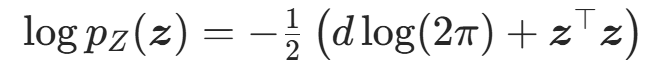
除高斯分布外，均匀分布、拉普拉斯分布也可作为基分布，核心要求是采样和密度计算高效。

（2）流（Flow）------ 可逆变换的复合

"流" 指K 个连续的、可逆的、雅可比行列式易计算的光滑变换 的复合，记为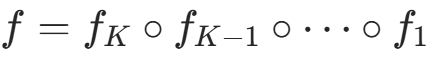，其中：

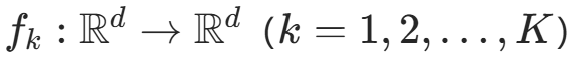：第k个可逆变换，称为流层；
：复合运算符，；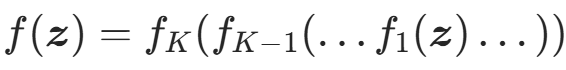
整体变换f：从基分布空间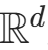到目标分布空间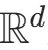的全局可逆变换 ，其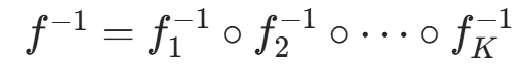（逆变换的复合顺序与正变换相反）。

核心优势 ：复合变换的可逆性由每个流层的可逆性 保证，复合变换的雅可比行列式由行列式的乘积性质计算，即：

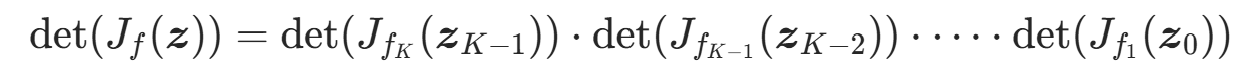
其中。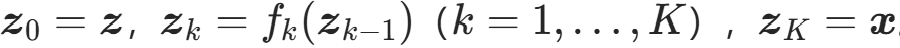

该性质让高维复合变换的雅可比行列式计算 分解为K 个流层雅可比行列式的乘积，只要每个流层的雅可比行列式易计算，整体计算就高效，这是标准化流能落地的关键。

2. 两个核心操作（模型的核心功能）

标准化流的所有应用都依赖密度估计 和采样两个核心操作，两者均通过上述定义的基分布和复合变换实现，无任何近似。

（1）采样（Generation）------ 从基分布到目标分布

采样是生成符合真实数据分布样本的过程，正向执行复合变换即可，步骤为：

从基分布中采样一个随机样本；
依次执行 K 个流层的正变换：；
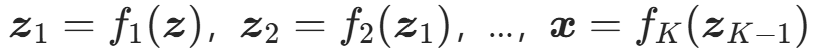输出x，即为目标分布的样本，即。

特点：采样过程是前向传播，无迭代、无近似，部分标准化流模型（如 RealNVP、Glow）的采样效率极高，与 GAN 相当。

（2）密度估计（Density Estimation）------ 计算样本的精确密度

密度估计是计算任意样本x在目标分布中的概率密度（或对数似然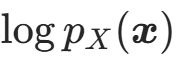）的过程，反向执行复合变换 + 利用对数似然核心公式，步骤为：

对输入样本x，依次执行 K 个流层的逆变换，得到基分布样本；
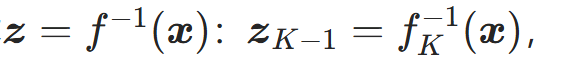
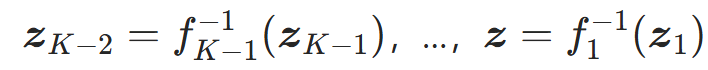计算基分布在z处的对数似然；
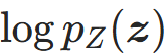计算每个流层在对应位置的雅可比行列式的对数绝对值，求和得到整体的对数行列式：；
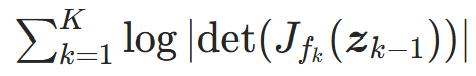代入对数似然核心公式 ，得到样本x的对数似然：
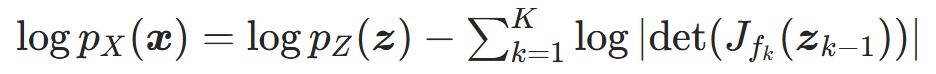
若需要概率密度，直接取指数即可：。

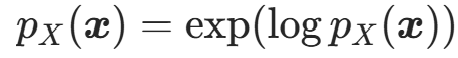特点：密度估计是反向传播，每一步都有精确计算，无任何近似，这是标准化流最核心的优势。

3. 标准化流的整体框架图

用简洁的流程图标注核心逻辑，直观理解模型的双向过程：

bash 复制代码

【采样流程（生成）】
基分布采样 z ~ p_Z(z) → 流层1 f1 → z1 → 流层2 f2 → z2 → ... → 流层K fK → x ~ p_X(x)（生成样本）

【密度估计流程】
输入样本 x → 逆流层K fK⁻¹ → zK-1 → 逆流层K-1 fK-1⁻¹ → zK-2 → ... → 逆流层1 f1⁻¹ → z = f⁻¹(x)
→ 计算log p_Z(z) → 计算各流层log|det(J_fk)|并求和 → 代入公式得log p_X(x)（精确对数密度）

五、标准化流的关键设计原则

并非所有可逆变换都适合作为标准化流的流层，设计流层时必须遵循两大核心原则，这是模型能高效训练和推理的前提，也是区分 "好的流" 和 "差的流" 的关键。

原则 1：变换必须可逆

可逆性是标准化流的必要条件，原因有二：

密度估计需要通过逆变换将样本x映射回基分布样本z，若无逆变换，无法计算；
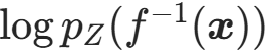生成的可控性依赖逆变换，通过调整基分布样本z，可精准控制生成样本x的特征，若无逆变换，这种双向映射关系消失。

工程实现 ：流层的可逆性需满足数学上的可逆条件 （如雅可比矩阵非奇异），且逆变换的计算效率要高（不能比正变换复杂太多）。

原则 2：雅可比行列式必须易计算（低计算复杂度）

高维数据（如图像256×256=65536维）的雅可比矩阵是d×d的方阵，直接计算其行列式的时间复杂度为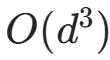，高维下完全不可行。

因此，流层的雅可比行列式必须满足 **"可分解、可简化、计算复杂度为 O (d) 或 O (1)"，即通过设计特殊的变换结构，让雅可比矩阵成为对角矩阵、三角矩阵、稀疏矩阵 ** 等特殊矩阵 ------ 这类矩阵的行列式计算极其简单（对角矩阵的行列式是对角线元素的乘积，三角矩阵的行列式是对角线元素的乘积）。

核心目标 ：将整体雅可比行列式的计算复杂度从O(d3)降低到线性复杂度 O (d)，让标准化流能处理高维数据。

补充原则：变换需具备足够的表达能力

流层的设计需保证复合变换f能拟合复杂的非线性分布（如自然图像、语音的分布），若变换过于简单（如仅线性变换），则复合变换仍为线性变换，只能拟合高斯分布，无法建模真实数据的复杂分布。

因此，流层通常是非线性可逆变换 ，通过堆叠足够多的非线性流层，让复合变换具备强大的非线性表达能力，这是模型能拟合真实数据分布的充分条件。

六、经典流层变换与主流标准化流模型

标准化流的发展历程，本质是流层变换的设计演进------ 从早期的简单非线性流层（表达能力有限），到现代的结构化流层（兼顾可逆性、雅可比计算效率和表达能力）。

下面从经典基础流层 （理解核心设计思想）和主流标准化流模型（工业界 / 学术界常用）两部分讲解，聚焦核心设计和优势。

1. 经典基础流层（早期简单变换）

早期的标准化流层设计简单，主要用于验证模型的可行性，虽表达能力有限，但能直观理解流层的设计原则，是后续复杂流层的基础。

（1）平面流（Planar Flow）

Planar Flow 是最经典的非线性可逆流层之一，由 Rezende et al. 在 2015 年提出，流层变换为：

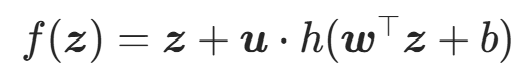
其中：

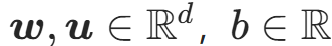：流层的可学习参数；
h(⋅)：光滑的非线性激活函数（如 tanh）；
可逆性条件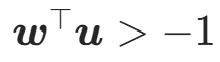：（保证雅可比矩阵非奇异）；
雅可比行列式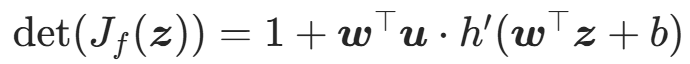：（计算复杂度 O (d)）。

特点：设计简单、可逆性条件明确、雅可比计算高效，但表达能力弱，需要堆叠大量流层才能拟合复杂分布，高维下效果差。

（2）径向流（Radial Flow）

Radial Flow 与 Planar Flow 同期提出，是另一类简单非线性流层，变换为：

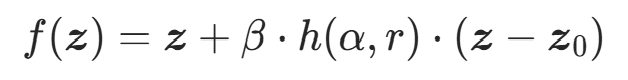
其中：

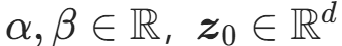：可学习参数；
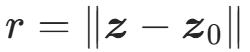：样本到中心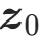的欧氏距离；
h(α,r)：非线性函数（如h=1/(α+r)）；
雅可比行列式：可分解为标量的乘积，计算复杂度 O (d)。

特点：比 Planar Flow 的表达能力稍强，但仍属于全局单变换，高维下拟合复杂分布的能力有限，仅适合低维数据（如 d<10）。

2. 主流标准化流模型（现代结构化变换）

现代标准化流模型的核心创新是结构化流层设计 ，通过特征分块、耦合变换、可逆卷积 等策略，兼顾可逆性、雅可比计算效率和非线性表达能力，能处理高维数据（如图像），是目前的主流选择。

（1）RealNVP（Real-valued Non-Volume Preserving Flow）

RealNVP 由 Dinh et al. 在 2016 年提出，是第一个能处理高维图像数据的标准化流模型 ，核心设计是耦合层（Coupling Layer），解决了高维下非线性可逆变换的设计难题。

核心：耦合层（Coupling Layer）

耦合层的核心思想是 **"特征分块 + 固定一块变换另一块"，将 d 维特征z分为两个不相交的子集和（如前 d/2 维为，后 d/2 维为），变换分为 缩放（scale）和平移（shift）两步，以正向变换 ** 为例：

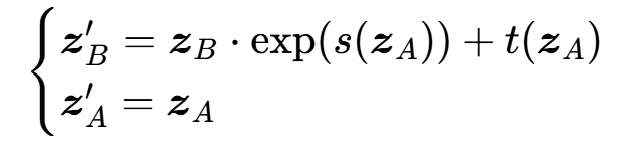
其中：

s(⋅),t(⋅)：由神经网络（如CNN、MLP）实现的非线性函数，分别输出缩放因子 和平移因子 ，仅依赖****；
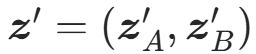：变换后的特征。

关键性质

可逆性 ：逆变换只需反向执行缩放和平移，计算简单：
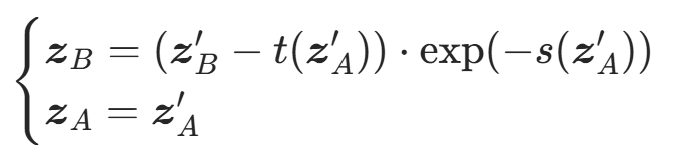
雅可比行列式易计算 ：雅可比矩阵为分块三角矩阵，行列式是对角线元素的乘积，即：

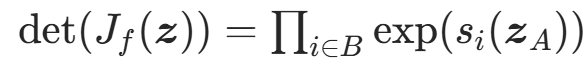
其中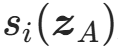是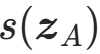的第i个分量，计算复杂度O(d)。

RealNVP的优化

交替分块 ：堆叠多个耦合层时，交替交换**** 和**** 的位置（如第1层变换**** ，第2层变换****），保证所有特征都被非线性变换；
归一化层：加入可逆的批归一化（Batch Normalization）和层归一化（Layer Normalization），提升模型的表达能力和训练稳定性；
CNN适配：将耦合层与CNN结合，实现对图像数据的建模（如处理MNIST、CIFAR-10）。

特点：表达能力强、训练高效、采样速度快，是标准化流的工业界基础模型 ，但分块设计导致特征交互不充分（仅块间交互，块内无交互）。

（2）Glow（Generative Flow with Invertible 1x1 Convolutions）

Glow由Kingma et al.在2018年提出，是RealNVP的升级版 ，核心创新是引入可逆1x1卷积（Invertible 1x1 Convolution） ，解决了RealNVP特征交互不充分的问题，进一步提升了模型的表达能力，是目前最常用的图像标准化流模型。

核心创新1：可逆1x1卷积

在耦合层之前加入可逆1x1卷积 ，作为独立的流层，作用是对特征进行线性混合 ，实现所有特征维度之间的充分交互。

可逆1x1卷积的变换为：

z′=W⋅z

其中W∈Rd×d是可逆的1x1卷积核 （方阵，）。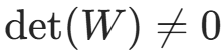

关键性质：

可逆性：逆变换为；
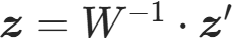雅可比行列式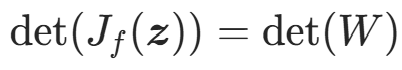：（与z无关，计算复杂度O(1)）；
可学习：W是模型的可学习参数，训练过程中自动学习最优的特征混合方式。

核心创新2：单分块耦合层（Squeeze-and-Excitation）

Glow简化了RealNVP的耦合层设计，采用单分块策略 ，并引入Squeeze操作（将图像的空间维度与通道维度交换，提升特征的维度利用率），进一步提升了模型的表达能力和计算效率。

特点：特征交互充分、表达能力强、适合高维图像生成（如CIFAR-10、ImageNet小尺寸），采样速度快，是目前标准化流中图像生成的SOTA模型之一。

（3）MAF/IAF（自回归流，Autoregressive Flows）

MAF（Masked Autoregressive Flow）和IAF（Inverse Autoregressive Flow）是基于自回归模型的标准化流 ，由Papamakarios et al.在2017年提出，核心设计是自回归变换 ，适合序列数据建模（如文本、语音、时间序列）。

核心思想

自回归流的流层是自回归可逆变换，即特征的第i个分量的变换仅依赖前i−1个分量，以一维变换为例：

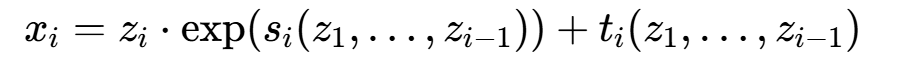
其中是自回归神经网络（如MADE、Transformer）实现的非线性函数。

关键性质

可逆性 ：逆变换为自回归的逆过程，；
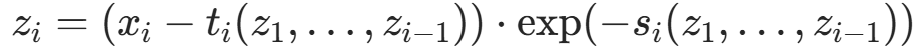雅可比行列式 ：雅可比矩阵为下三角矩阵，行列式是对角线元素的乘积，计算效率高；
自回归特性：适合序列数据的建模，能捕捉序列的时序依赖关系。

MAF vs IAF

MAF：正变换是自回归的，采样过程为自回归（逐维生成，速度慢），密度估计过程高效；
IAF：逆变换是自回归的，采样过程高效（前向传播），密度估计过程为自回归（速度慢）。

特点：适合序列数据建模，表达能力强，能捕捉复杂的时序依赖，但采样/密度估计必有一个是自回归的，速度较慢。

七、标准化流的训练方法

标准化流的训练是有监督的概率密度估计问题 ，训练目标、损失函数、优化方法都非常标准化，训练稳定性远高于GAN，是概率生成模型中最易训练的类型之一。

1. 训练目标

核心训练目标是最大化训练数据集的对数似然（Maximum Likelihood Estimation，MLE），即找到最优的复合变换参数θ（所有流层的可学习参数），使得训练数据的对数似然之和最大：

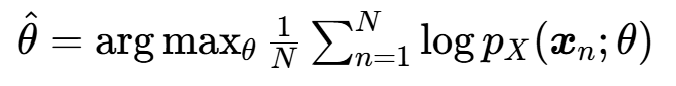
其中N是训练样本数，是第n个训练样本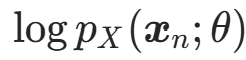，由对数似然核心公式计算。

2. 损失函数

由于深度学习框架通常采用梯度下降法 优化，因此将最大化对数似然转化为最小化负的平均对数似然（Negative Log-Likelihood，NLL），这是标准化流的唯一损失函数：

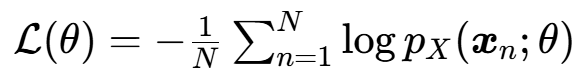
损失函数越小，说明模型拟合真实数据分布的效果越好。

3. 训练流程

标准化流的训练流程为批量梯度下降，步骤简单且可复现，以处理图像数据的Glow模型为例：

数据预处理：将训练图像归一化到 $-1,1$ （适配流层的非线性变换），按批次划分；
模型初始化：初始化基分布（标准高斯）、所有流层的参数（如耦合层的CNN、可逆1x1卷积核）；
前向计算（密度估计） ：对每个批次的样本，执行密度估计的反向变换流程，计算每个样本的对数似然logpX(x)，进而计算批次的NLL损失；
反向传播与参数更新：计算损失函数对所有可学习参数的梯度，通过优化器（如Adam、SGD）更新参数；
迭代训练：重复步骤3-4，直到损失函数收敛（或达到最大训练轮数）；
模型验证：用验证集的NLL损失评估模型性能，选择验证集损失最小的模型作为最终模型。

4. 优化技巧

梯度裁剪（Gradient Clipping）：高维下雅可比行列式的对数可能出现梯度爆炸，通过梯度裁剪将梯度限制在一定范围内，提升训练稳定性；
学习率衰减：采用余弦退火、阶梯衰减等学习率调度策略，让模型在训练后期更稳定地收敛；
归一化层：在流层中加入可逆的批归一化、层归一化，加速训练收敛，提升模型表达能力；
小批次训练：标准化流对批次大小不敏感，可采用小批次训练，降低内存占用。

八、标准化流的优缺点

标准化流作为概率生成模型的重要分支，其优缺点与设计原则高度相关，优势体现在概率密度的精确性和训练的稳定性 ，缺点则体现在高维数据的建模难度和表达能力的限制。

核心优点

精确的概率密度估计：无任何近似，可直接计算样本的对数似然，适合异常检测（通过密度值判断是否为异常）、概率预测（如预测样本的生成概率）等场景；
训练稳定：训练目标是最小化NLL损失，属于有监督的优化问题，无GAN的模式崩溃、梯度消失问题，也无VAE的变分下界近似偏差，调参简单；
可逆的生成与推断 ：变换的可逆性让"隐变量-样本"双向映射，可实现可控生成（如通过调整基分布的高斯样本，控制生成图像的颜色、形状等特征）；
无模式崩溃：对数似然的优化目标会让模型尽可能拟合所有数据的分布，不会出现只拟合部分数据模式的问题；
采样高效（部分模型）：如RealNVP、Glow等模型的采样过程是前向传播，无迭代，采样速度与GAN相当。

核心缺点

高维数据建模难度大：流层的设计需兼顾可逆性、雅可比计算效率和表达能力，高维下（如256×256图像）需要堆叠大量流层，导致模型参数量大、训练时间长；
表达能力受限于变换序列：复合变换的表达能力依赖流层的数量和类型，若流层数量不足或类型简单，无法拟合真实数据的复杂分布；
部分模型采样/密度估计效率低：如自回归流（MAF/IAF）的采样或密度估计是自回归的，逐维计算，速度较慢；
内存占用高：训练过程中需要存储每个流层的中间结果（用于计算雅可比行列式），高维下内存占用较大；
对数据分布的假设较强：假设真实数据分布与基分布之间存在一系列可逆的光滑变换，若该假设不成立，模型拟合效果会变差。

九、标准化流的应用场景

标准化流的应用场景主要围绕**"精确密度估计"和 "可控生成"两大核心优势展开，尤其适合对 概率密度计算精度有要求或需要可控生成的场景，在机器学习、计算机视觉、自然语言处理、计算生物学、强化学习**等领域均有广泛应用。

1. 密度估计与异常检测

这是标准化流最经典的应用场景，通过计算样本的概率密度值，判断样本是否为异常：

工业质检：对产品图像进行密度估计，密度值低于阈值的图像判定为次品；
网络安全：对网络流量、用户行为进行密度估计，密度值异常的行为判定为攻击行为；
医疗诊断：对医学影像（如CT、MRI）、生理信号（如心电图）进行密度估计，密度值异常的样本判定为患病样本。

2. 可控生成建模

利用"隐变量-样本"的双向可逆映射，实现可控的生成：

图像生成：如RealNVP、Glow可生成高质量的手写数字（MNIST）、自然图像（CIFAR-10），并通过调整基分布的高斯样本，控制生成图像的特征（如颜色、形状、视角）；
分子生成：在计算生物学中，标准化流可生成符合特定化学性质的分子结构（如药物分子），通过调整隐变量控制分子的溶解度、活性等性质；
语音合成：结合自回归流，可生成高质量的语音信号，并控制语音的语速、语调、音色。

3. 变分推断（Variational Inference）

标准化流可作为变分推断的近似后验分布，替代VAE中的简单高斯后验，提升变分推断的精度：

VAE+NF：将标准化流应用于VAE的隐变量空间，让近似后验分布更接近真实后验分布，提升VAE的生成质量和密度估计精度；
贝叶斯推理：在贝叶斯模型中，用标准化流建模复杂的后验分布，实现高效的贝叶斯推理。

4. 强化学习（Reinforcement Learning）

标准化流可用于强化学习的策略建模，替代传统的高斯策略，提升策略的表达能力：

策略梯度：用标准化流建模策略分布（动作的条件分布），能拟合更复杂的策略分布，提升智能体的决策能力；
离线强化学习：用标准化流对离线数据进行密度估计，筛选高质量的离线数据，提升离线强化学习的性能。

5. 序列数据建模

自回归流（MAF/IAF）适合序列数据的建模，能捕捉复杂的时序依赖关系：

文本生成：结合Transformer构建自回归流，生成高质量的文本序列；
时间序列预测：对时间序列数据进行密度估计，实现概率性的时间序列预测（如预测未来的股票价格、气象数据）。

十、标准化流模型（NF）的Python代码完整实现

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from torch.distributions import MultivariateNormal
from typing import List, Tuple

# 设备配置：优先GPU，无则CPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 随机种子：保证实验可复现
torch.manual_seed(42)
np.random.seed(42)


class Flow(nn.Module):
    """标准化流基类：定义所有流层必须实现的核心接口"""

    def __init__(self):
        super().__init__()

    def forward(self, z: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """
        正向变换：z → x（基分布→目标分布，生成过程）
        :param z: 基分布样本，shape=[batch_size, dim]
        :return: (x: 变换后样本, log_det: 正向变换的对数雅可比行列式，shape=[batch_size])
        """
        raise NotImplementedError("所有流层必须实现forward方法")

    def inverse(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """
        反向变换：x → z（目标分布→基分布，密度估计过程）
        :param x: 目标分布/真实数据样本，shape=[batch_size, dim]
        :return: (z: 逆变换后基分布样本, log_det: 反向变换的对数雅可比行列式，shape=[batch_size])
        """
        raise NotImplementedError("所有流层必须实现inverse方法")


class PlanarFlow(Flow):
    """平面流（Planar Flow）：经典低维非线性流层，适合d≤10的低维数据"""

    def __init__(self, dim: int):
        """
        :param dim: 数据维度（本文用dim=2）
        """
        super().__init__()
        self.dim = dim
        # 初始化可学习参数：w, u ∈ R^d，b ∈ R
        self.w = nn.Parameter(torch.randn(1, dim, device=device))
        self.u = nn.Parameter(torch.randn(1, dim, device=device))
        self.b = nn.Parameter(torch.randn(1, device=device))
        # 激活函数选tanh（光滑可微，符合理论要求），其导数为1-tanh²(x)
        self.h = torch.tanh
        self.h_prime = lambda x: 1 - torch.tanh(x) ** 2

    def _enforce_invertibility(self) -> torch.Tensor:
        """保证可逆性条件：w^T u > -1，通过变换u实现"""
        wu = torch.matmul(self.w, self.u.T)  # shape=[1,1]
        # 用softplus保证：w^T u + 1 > 0 → w^T u > -1
        u_hat = self.u + (torch.log(1 + torch.exp(wu)) - 1 - wu) * self.w / (
                    torch.norm(self.w) ** 2 + 1e-8)  # 加epsilon避免除0
        return u_hat

    def forward(self, z: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """正向变换：z → x，返回x和正向变换的log|det(J_f)|"""
        u_hat = self._enforce_invertibility()  # 保证可逆性
        wz_b = torch.matmul(z, self.w.T) + self.b  # shape=[batch_size, 1]
        h_wz_b = self.h(wz_b)
        # 平面流正向变换公式
        x = z + u_hat * h_wz_b
        # 计算log|det(J_f)|：对应理论公式的对数形式
        psi = self.h_prime(wz_b) * self.w  # shape=[1, dim]
        log_det = torch.log(torch.abs(1 + torch.matmul(psi, u_hat.T)) + 1e-8)  # +1e-8避免数值为0
        # 先挤压为1维，再扩展为batch维度（解决维度不匹配报错）
        log_det = log_det.squeeze().expand(z.shape[0])
        return x, log_det

    def inverse(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """平面流逆变换：x → z（数值迭代法，因无解析逆），返回z和反向变换的log|det(J_f^{-1})|"""
        # 平面流无解析逆变换，用固定点迭代法求解z（低维下收敛快）
        z = x.clone()
        for _ in range(50):  # 迭代50次足够收敛
            u_hat = self._enforce_invertibility()
            wz_b = torch.matmul(z, self.w.T) + self.b
            z = x - u_hat * self.h(wz_b)
        # 反向变换的log|det(J_f^{-1})| = -正向变换的log|det(J_f)|（行列式逆性质）
        _, log_det_forward = self.forward(z)
        log_det_inverse = -log_det_forward
        return z, log_det_inverse


class CouplingLayer(Flow):
    """耦合层（Coupling Layer）：RealNVP核心，适合高维数据，本文实现二维版本"""

    def __init__(self, dim: int, mask: torch.Tensor, hidden_dim: int = 32):
        """
        :param dim: 数据维度
        :param mask: 分块掩码，0表示变换块（z_B），1表示固定块（z_A），shape=[dim]
        :param hidden_dim: MLP隐藏层维度，用于实现s(缩放)和t(平移)函数
        """
        super().__init__()
        self.dim = dim
        self.mask = mask.to(device)  # 掩码固定，不参与训练

        # 用MLP实现s和t函数：输入固定块z_A，输出缩放因子s和平移因子t（维度与变换块z_B一致）
        self.mlp = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, 2 * dim)  # 输出2*dim，分别对应s和t
        ).to(device)

        # 初始化最后一层权重为0，保证初始变换为恒等变换（训练更稳定）
        nn.init.constant_(self.mlp[-1].weight, 0.0)
        nn.init.constant_(self.mlp[-1].bias, 0.0)

    def forward(self, z: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """正向变换：z → x，mask=1的维度固定，mask=0的维度缩放平移"""
        z_A = z * self.mask  # 固定块（不变换）
        z_B = z * (1 - self.mask)  # 变换块（缩放+平移）
        # MLP输出s和t
        s_t = self.mlp(z_A)
        s = s_t[:, :self.dim] * (1 - self.mask)  # s仅作用于变换块
        t = s_t[:, self.dim:] * (1 - self.mask)  # t仅作用于变换块

        # 限制s的范围，避免exp(s)数值爆炸（数值稳定化关键）
        s = torch.tanh(s) * 0.5  # 把s限制在[-0.5, 0.5]，exp(s)∈[0.606, 1.648]

        # 变换块正向计算：z_B' = z_B * exp(s) + t，加小epsilon避免数值异常
        z_B_prime = z_B * torch.exp(s + 1e-8) + t
        # 拼接得到x
        x = z_A + z_B_prime
        # 计算log|det(J_f)|：仅为变换块s的和（对应理论公式）
        log_det = torch.sum(s, dim=1)
        return x, log_det

    def inverse(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """反向变换：x → z，解析逆，计算高效（耦合层核心优势）"""
        x_A = x * self.mask  # 固定块，与正向一致
        x_B = x * (1 - self.mask)  # 变换块，需反向计算
        # MLP输出s和t（输入固定块，与正向一致）
        s_t = self.mlp(x_A)
        s = s_t[:, :self.dim] * (1 - self.mask)
        t = s_t[:, self.dim:] * (1 - self.mask)

        # 和正向保持一致，限制s的范围
        s = torch.tanh(s) * 0.5

        # 变换块逆计算：z_B = (x_B - t) * exp(-s)，加小epsilon避免数值异常
        z_B = (x_B - t) * torch.exp(-s + 1e-8)
        # 拼接得到z
        z = x_A + z_B
        # 反向变换的log|det(J_f^{-1})| = -正向log|det(J_f)|
        log_det = -torch.sum(s, dim=1)
        return z, log_det


# 定义复合流：堆叠多个流层，自动累加对数行列式（标准化流的核心组合方式）
class SequentialFlow(nn.Module):
    def __init__(self, flows: List[Flow]):
        super().__init__()
        self.flows = nn.ModuleList(flows)

    def forward(self, z: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """正向变换：堆叠流层，累加log_det"""
        x = z
        total_log_det = torch.zeros(z.shape[0], device=device)
        for flow in self.flows:
            x, log_det = flow.forward(x)
            total_log_det += log_det
        return x, total_log_det

    def inverse(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        """反向变换：逆序堆叠流层，累加log_det"""
        z = x
        total_log_det = torch.zeros(x.shape[0], device=device)
        for flow in reversed(self.flows):
            z, log_det = flow.inverse(z)
            total_log_det += log_det
        # 裁剪z的极值，避免数值爆炸（针对网格点的外推）
        z = torch.clamp(z, min=-10.0, max=10.0)
        return z, total_log_det


def generate_data(n_samples: int = 1000, noise: float = 0.05) -> torch.Tensor:
    """
    生成二维月牙形数据，归一化到[-2,2]
    :param n_samples: 样本数
    :param noise: 噪声强度
    :return: 形状为[n_samples, 2]的张量，设备与配置一致
    """
    # 生成第一个半圆弧（上半月）
    theta1 = np.linspace(0, np.pi, n_samples // 2)
    x1 = np.cos(theta1)
    y1 = np.sin(theta1)
    moon1 = np.column_stack([x1, y1]) + np.random.normal(0, noise, (n_samples // 2, 2))

    # 生成第二个半圆弧（下半月，偏移后）
    theta2 = np.linspace(0, np.pi, n_samples - n_samples // 2)
    x2 = 1 - np.cos(theta2)
    y2 = 0.5 - np.sin(theta2)
    moon2 = np.column_stack([x2, y2]) + np.random.normal(0, noise, (n_samples - n_samples // 2, 2))

    # 合并两个月牙，缩放至[-2,2]区间（与原sklearn版本一致）
    moons = np.vstack([moon1, moon2])
    moons = moons * 2  # 放大到[-2,2]
    # 转换为张量，指定设备
    moons_tensor = torch.tensor(moons, dtype=torch.float32, device=device)
    return moons_tensor


def train_flow(model: nn.Module, data: torch.Tensor, epochs: int = 5000, lr: float = 1e-3):
    """训练标准化流：目标为最小化负对数似然（NLL）"""
    optimizer = optim.Adam(model.parameters(), lr=lr)
    # 基分布：标准二维高斯（MultivariateNormal）
    base_dist = MultivariateNormal(torch.zeros(2, device=device), torch.eye(2, device=device))
    model.train()

    for epoch in range(epochs):
        optimizer.zero_grad()
        # 密度估计流程：真实数据x → 逆变换→z + 累加log_det
        z, log_det_inverse = model.inverse(data)
        # 计算对数似然：log p_X(x) = log p_Z(z) + log_det_inverse（对应核心公式）
        log_p_x = base_dist.log_prob(z) + log_det_inverse
        # 损失函数：负平均对数似然（NLL）
        loss = -torch.mean(log_p_x)
        # 反向传播+参数更新
        loss.backward()

        # 梯度裁剪，防止梯度爆炸导致参数飞掉（训练稳定化关键）
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

        optimizer.step()

        # 每500轮打印一次损失
        if (epoch + 1) % 500 == 0:
            print(f"Epoch [{epoch + 1}/{epochs}], Loss (NLL): {loss.item():.4f}")
    return model


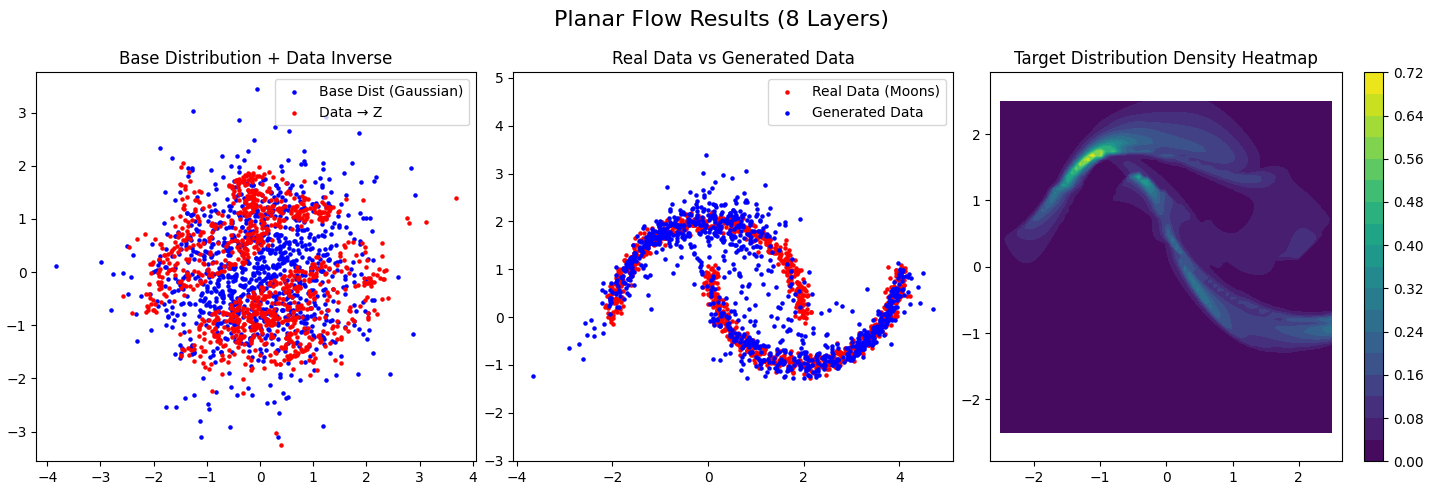
def visualize_results(model: nn.Module, data: torch.Tensor, title: str):
    """可视化：1.基分布生成样本；2.真实数据逆变换；3.目标分布密度热力图"""
    base_dist = MultivariateNormal(torch.zeros(2, device=device), torch.eye(2, device=device))
    model.eval()
    with torch.no_grad():
        # 1. 生成样本：基分布z → 正向变换→x（生成过程）
        z_sample = base_dist.sample((1000,))
        x_sample, _ = model.forward(z_sample)
        # 2. 真实数据逆变换：x → 逆变换→z
        z_data, _ = model.inverse(data)

    # 画图设置
    fig, axes = plt.subplots(1, 3, figsize=(18, 5))
    fig.suptitle(title, fontsize=16)
    # 子图1：基分布样本 + 真实数据逆变换后的z
    axes[0].scatter(z_sample[:, 0].cpu().numpy(), z_sample[:, 1].cpu().numpy(), c='blue', s=5,
                    label='Base Dist (Gaussian)')
    axes[0].scatter(z_data[:, 0].cpu().numpy(), z_data[:, 1].cpu().numpy(), c='red', s=5, label='Data → Z')
    axes[0].set_title('Base Distribution + Data Inverse')
    axes[0].legend()
    axes[0].axis('equal')

    # 子图2：真实数据 + 模型生成样本
    axes[1].scatter(data[:, 0].cpu().numpy(), data[:, 1].cpu().numpy(), c='red', s=5, label='Real Data (Moons)')
    axes[1].scatter(x_sample[:, 0].cpu().numpy(), x_sample[:, 1].cpu().numpy(), c='blue', s=5, label='Generated Data')
    axes[1].set_title('Real Data vs Generated Data')
    axes[1].legend()
    axes[1].axis('equal')

    # 缩小网格点范围，贴合训练数据的[-2,2]，避免外推导致的数值异常
    x = np.linspace(-2.5, 2.5, 80)  # 从[-3,3]→[-2.5,2.5]，减少外推
    y = np.linspace(-2.5, 2.5, 80)
    X_grid, Y_grid = np.meshgrid(x, y)
    grid = torch.tensor(np.c_[X_grid.ravel(), Y_grid.ravel()], dtype=torch.float32, device=device)
    with torch.no_grad():
        z_grid, log_det_grid = model.inverse(grid)
        log_p_grid = base_dist.log_prob(z_grid) + log_det_grid

        # 替换NaN/无穷大值，保证热力图正常绘制
        p_grid = torch.exp(log_p_grid)
        p_grid = torch.clamp(p_grid, min=0.0,
                             max=p_grid[~torch.isnan(p_grid)].max() if len(p_grid[~torch.isnan(p_grid)]) > 0 else 1.0)
        p_grid[torch.isnan(p_grid)] = 0.0
        p_grid[torch.isinf(p_grid)] = 0.0
        p_grid = p_grid.cpu().numpy().reshape(X_grid.shape)

    im = axes[2].contourf(X_grid, Y_grid, p_grid, cmap='viridis', levels=20)
    plt.colorbar(im, ax=axes[2])
    axes[2].set_title('Target Distribution Density Heatmap')
    axes[2].axis('equal')

    plt.tight_layout()
    plt.show()


# ---------------------- 主程序：训练并可视化两种模型 ----------------------
if __name__ == "__main__":
    # 1. 生成训练数据（纯NumPy，无sklearn）
    data = generate_data(n_samples=1000)

    # 2. 模型1：堆叠8层平面流（Planar Flow）
    print("=" * 50, "训练平面流模型", "=" * 50)
    planar_flows = [PlanarFlow(dim=2) for _ in range(8)]
    planar_model = SequentialFlow(planar_flows).to(device)
    planar_model = train_flow(planar_model, data, epochs=5000, lr=1e-3)
    visualize_results(planar_model, data, title="Planar Flow Results (8 Layers)")

    # 3. 模型2：堆叠4层耦合层（Coupling Layer）→ 简易RealNVP（交替分块掩码）
    print("\n" + "=" * 50, "训练简易RealNVP模型", "=" * 50)
    dim = 2
    # 交替掩码：保证所有维度被变换（第1层掩码[1,0]，第2层[0,1]，循环）
    masks = [torch.tensor([1.0, 0.0]), torch.tensor([0.0, 1.0])] * 2
    coupling_flows = [CouplingLayer(dim=2, mask=mask) for mask in masks]
    realnvp_model = SequentialFlow(coupling_flows).to(device)
    realnvp_model = train_flow(realnvp_model, data, epochs=5000, lr=1e-3)
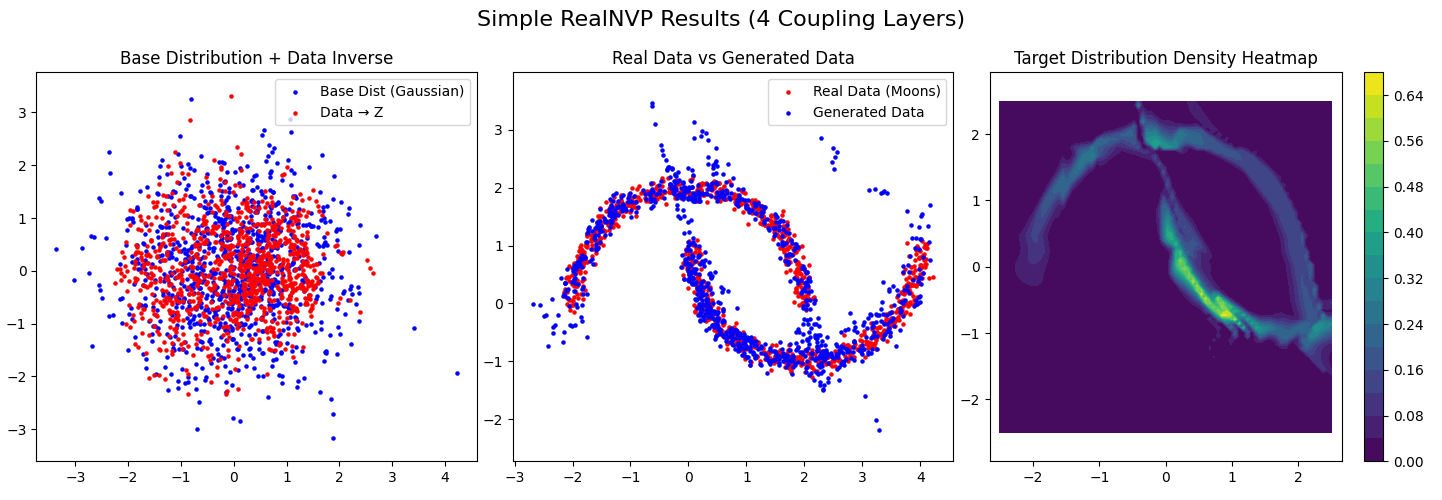
    visualize_results(realnvp_model, data, title="Simple RealNVP Results (4 Coupling Layers)")

十一、程序运行结果展示

================================================== 训练平面流模型 ==================================================

Epoch $500/5000$ , Loss (NLL): 2.9427

Epoch $1000/5000$ , Loss (NLL): 2.7024

Epoch $1500/5000$ , Loss (NLL): 2.3728

Epoch $2000/5000$ , Loss (NLL): 2.2443

Epoch $2500/5000$ , Loss (NLL): 2.1608

Epoch $3000/5000$ , Loss (NLL): 2.0992

Epoch $3500/5000$ , Loss (NLL): 2.0536

Epoch $4000/5000$ , Loss (NLL): 2.0178

Epoch $4500/5000$ , Loss (NLL): 1.9986

Epoch $5000/5000$ , Loss (NLL): 1.9890

================================================== 训练简易RealNVP模型 ==================================================

Epoch $500/5000$ , Loss (NLL): 2.0218

Epoch $1000/5000$ , Loss (NLL): 1.9442

Epoch $1500/5000$ , Loss (NLL): 1.9229

Epoch $2000/5000$ , Loss (NLL): 1.9106

Epoch $2500/5000$ , Loss (NLL): 1.8984

Epoch $3000/5000$ , Loss (NLL): 1.8886

Epoch $3500/5000$ , Loss (NLL): 1.8787

Epoch $4000/5000$ , Loss (NLL): 1.8706

Epoch $4500/5000$ , Loss (NLL): 1.8656

Epoch $5000/5000$ , Loss (NLL): 1.8575

十二、总结与发展趋势

核心总结

标准化流是基于可逆概率密度变换的显式概率生成模型 ，核心思想是通过简单基分布 和一系列可逆变换 ，实现对复杂目标分布的精确密度估计 和可控采样 。其核心优势是概率密度的精确性、训练的稳定性和生成的可控性 ，核心约束是流层的设计需兼顾可逆性、雅可比计算效率和表达能力。

与GAN、VAE、扩散模型相比，标准化流的核心价值在于精确的密度估计，这是其他生成模型无法替代的，因此在对密度精度有要求的场景（如异常检测、概率预测）中具有不可替代的地位。

未来发展趋势

更高效的高维流层设计：研究更简洁、更高效的高维可逆变换，降低模型参数量和训练时间，提升高维数据（如高清图像）的建模能力；
与其他生成模型的融合 ：如流+扩散模型 （用流提升扩散模型的采样效率）、流+GAN （用流为GAN引入显式密度估计）、流+VAE（用流提升VAE的后验精度），结合各模型的优势；
自适应流层与动态流：研究能根据数据分布自适应调整流层数量和类型的动态流，提升模型的泛化能力；
大模型与标准化流的结合：将标准化流与Transformer、大语言模型（LLM）结合，实现对超大规模序列数据的建模和可控生成；
实际场景的落地优化：针对工业质检、医疗诊断、分子生成等实际场景，优化标准化流的模型结构和训练策略，提升模型的实用性和效率。

标准化流作为概率生成模型的基础分支，其核心的可逆变换 和概率密度变换思想已成为现代机器学习的重要工具，未来将在更多实际场景中发挥重要作用。