合并排序 merge sort

合并排序是一种以高效和稳定性著称的流行排序算法。它采用了分而治之的策略。它的工作原理是递归地将输入数组分成两半，递归地对两半进行排序，最后将它们合并回去，从而获得已排序的数组。

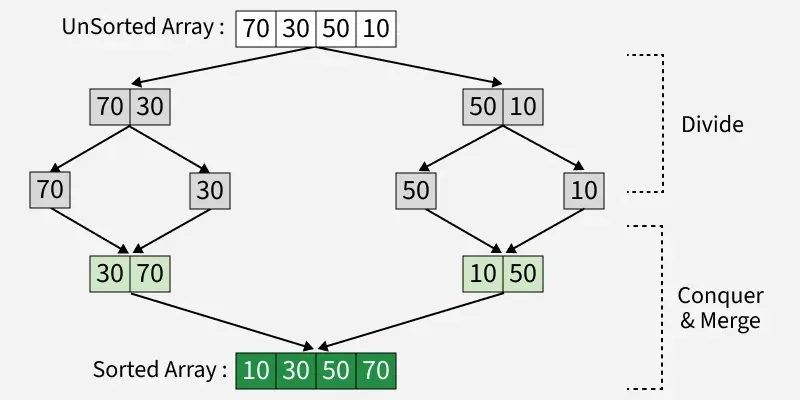
以下是合并排序的逐步解释：

除法：递归地将列表或数组分成两半，直到无法再分割为止。

征服：每个子数组都使用合并排序算法单独排序。

合并：排序后的子数组按排序顺序合并回。该过程持续进行，直到两个子数组的所有元素都被合并为止。

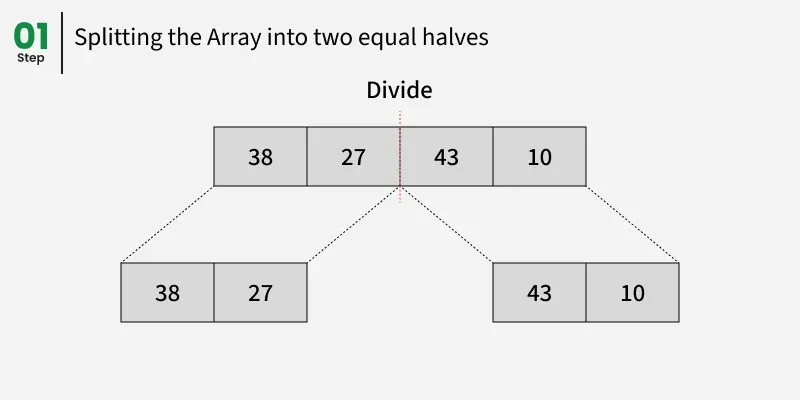
我们用合并排序来排序数组或列表 $38， 27， 43， 10$

让我们看看上述例子的工作原理：

划分：

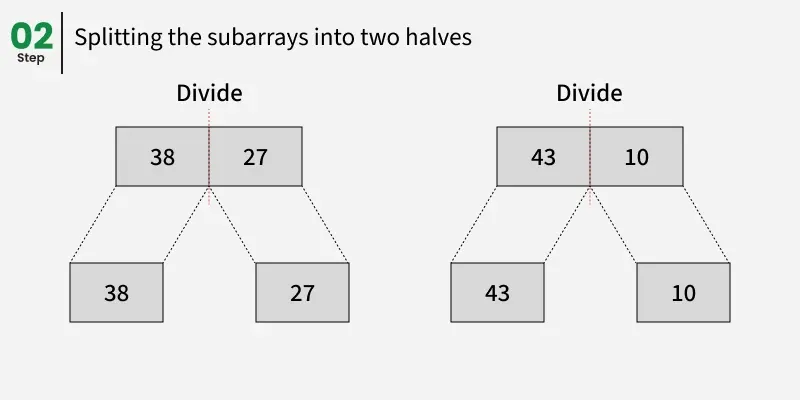
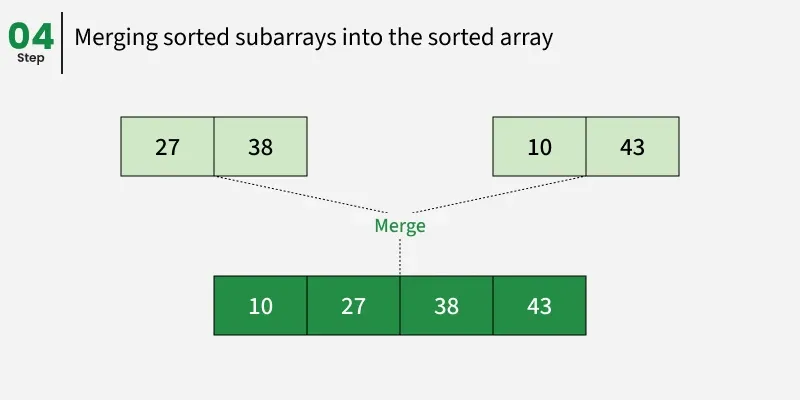
$38， 27， 43， 10$ 分为 $38， 27$ 和 $43， 10$ 。

$38， 27$ 分为 $38$ 和 $27$ 。

$43， 10$ 被划分为 $43$ 和 $10$ 。

征服：

$38$ 已经被安排好了。

$27$ 已经被安排好了。

$43$ 已经安排好了。

$10$ 已经解决了。

合并：

合并 $38$ 和 $27$ 即可得到 $27， 38$ 。

合并 $43$ 和 $10$ 即可得到 $10,43$ 。

合并 $27， 38$ 和 $10， 43$ 以获得最终排序列表 $10， 27， 38， 43$

因此，排序列表为 $10， 27， 38， 43$ 。

重定向图标

复制代码

function merge(arr, left, mid, right) {
    const n1 = mid - left + 1;
    const n2 = right - mid;

    // Create temp arrays
    const L = new Array(n1);
    const R = new Array(n2);

    // Copy data to temp arrays L[] and R[]
    for (let i = 0; i < n1; i++)
        L[i] = arr[left + i];
    for (let j = 0; j < n2; j++)
        R[j] = arr[mid + 1 + j];

    let i = 0, j = 0;
    let k = left;

    // Merge the temp arrays back into arr[left..right]
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // Copy the remaining elements of L[], if there are any
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    // Copy the remaining elements of R[], if there are any
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

function mergeSort(arr, left, right) {
    if (left >= right)
        return;

    const mid = Math.floor(left + (right - left) / 2);
    mergeSort(arr, left, mid);
    mergeSort(arr, mid + 1, right);
    merge(arr, left, mid, right);
}


// Driver code
const arr = [38, 27, 43, 10];
mergeSort(arr, 0, arr.length - 1);
console.log(arr.join(" "));

输出

10 27 38 43

合并排序的递发关系

合并排序的递归关系为：

合并排序的复杂性分析

时间复杂性：

最佳情况：O（n log n），当数组已经排序或接近排序时。

平均情况：O（n log n），当数组被随机排序时。

最坏情况：O（n log n），当数组按倒序排序时。

辅助空间：O（n），合并时临时阵列需要额外空间。

合并排序的应用：

对大型数据集进行排序

外部排序（当数据集太大无法放入内存时）

用于解决倒置计数、右边小数和超越计数等问题

合并排序及其变体被用于编程语言的库方法中。其变体 TimSort 被用于 Python、Java Android 和 Swift。偏好排序非原始类型的主要原因是稳定性，而快速排序中不存在。Java 中的 Arrays.sort 使用 QuickSort，而 Collections.sort 使用 MergeSort。

它是排序链表的首选算法。

它可以很容易并行化，因为我们可以独立排序子数组然后合并。

合并排序的合并函数用于高效解决两个已排序数组的并集和交集等问题。

合并排序的优缺点

优点

稳定性：合并排序是一种稳定排序算法，意味着它保持输入数组中相等元素的相对顺序。

保证最坏情况下性能：合并排序的最坏情况时间复杂度为 O（N logN），这意味着即使在大型数据集上也能表现出色。

易于实施：分而治之的方法非常直接。

自然并行：我们独立合并子数组，使其适合并行处理。

缺点

空间复杂度：合并排序在排序过程中需要额外内存来存储合并后的子数组。

非原地：合并排序不是原地排序算法，这意味着它需要额外的内存来存储已排序的数据。这在需要考虑内存使用的情况下可能是个缺点。

合并排序总体上比快速排序慢，因为快速排序更适合缓存，因为它可以原地使用。

复制代码

编程资源
https://pan.quark.cn/s/7f7c83756948
更多资源
https://pan.quark.cn/s/bda57957c548