灰度变换与阈值化:从像素映射到图像二值化的核心操作【计算机视觉】
- 灰度变换与阈值化
-
- Ⅰ、引言
- Ⅱ、灰度变换
-
- 一、点运算
- 二、灰度变换的常见类型
-
- [1. 线性灰度变换](#1. 线性灰度变换)
- [2. 非线性灰度变换](#2. 非线性灰度变换)
- [3. 分段灰度变换](#3. 分段灰度变换)
- 三、直方图均衡化与直方图匹配
-
- [1. 直方图均衡化](#1. 直方图均衡化)
- [2. 直方图匹配(直方图规定化)](#2. 直方图匹配(直方图规定化))
- Ⅲ、图像阈值化与二值化
-
- [一、 全局阈值化](#一、 全局阈值化)
- [二、 Otsu阈值化(最大类间方差法)](#二、 Otsu阈值化(最大类间方差法))
-
- [1. 核心数学原理](#1. 核心数学原理)
- [2. 算法特点](#2. 算法特点)
- [3. 适用场景](#3. 适用场景)
- [三、 自适应阈值化](#三、 自适应阈值化)
-
- [1. 核心原理](#1. 核心原理)
- [2. 常见类型](#2. 常见类型)
- [3. 算法特点](#3. 算法特点)
- [4. 适用场景](#4. 适用场景)
- [四、 二值化结果与应用](#四、 二值化结果与应用)
- Ⅳ、总结
灰度变换与阈值化
Ⅰ、引言
在计算机视觉的工作流程中,灰度变换与阈值化是最基础且关键的预处理步骤,是后续复杂任务的基石。它们的核心价值在于:
- 灰度变换:通过对像素灰度值的映射与调整,能有效增强图像对比度、压缩动态范围,让后续算法更容易捕捉关键信息。
- 阈值化:作为最经典的图像分割技术之一,它将灰度图像转化为仅包含前景与背景的二值图像,极大简化了目标轮廓提取、特征匹配等后续任务的计算复杂度。
从早期的全局固定阈值,到如今结合局部纹理与光照信息的自适应阈值算法,灰度变换与阈值化技术不断迭代。它们不仅在工业检测、医学影像分析等传统领域广泛应用,也是深度学习中数据预处理的重要环节。
注意:本文所有代码均可导入Jupyter Notebook
完整代码仓库地址:🔗 GitHub:https://github.com/KnifeWen007/CV---StudyNotebook
Ⅱ、灰度变换
作为阈值化的重要前置预处理步骤 ,灰度变换是典型的逐像素点运算 ,它仅调整像素的灰度明暗数值,不改变图像的空间位置与整体结构,通过灰度映射关系完成图像增强。
借助灰度变换可以有效提升图像对比度 、还原暗部/亮部隐藏细节,优化整体灰度分布,为后续阈值分割等操作降低处理难度。其常见实现方式包含线性、非线性、分段变换 ,以及典型的直方图均衡化 与直方图匹配算法。
一、点运算
点运算(又称像素点处理)是灰度变换的核心实现方式,本质是对图像中每个像素的灰度值,单独执行预设的数学映射函数 s = T ( r ) s=T(r) s=T(r)(其中 r r r 为原始灰度值, s s s 为变换后灰度值, T T T 为映射关系)。
式中各变量定义:
- r r r:原始输入灰度值 ,通常取值区间为 [ 0 , L − 1 ] \boldsymbol{[0,L-1]} [0,L−1],对8位灰度图, L = 256 L=256 L=256,即 r ∈ { 0 , 1 , 2 , ... , 255 } r\in\{0,1,2,\dots,255\} r∈{0,1,2,...,255};
- s s s:变换后输出灰度值 ,同样约束在 [ 0 , L − 1 ] \boldsymbol{[0,L-1]} [0,L−1] 内,保证为合法灰度;
- T ( ⋅ ) T(\cdot) T(⋅):灰度映射函数 ,是定义在 [ 0 , L − 1 ] [0,L-1] [0,L−1] 上的单值函数,每个输入 r r r 唯一对应一个输出 s s s。
其核心数学与运算特点:
- 点对点独立映射 :输出 s ( x , y ) s(x,y) s(x,y) 仅由当前像素的 r ( x , y ) r(x,y) r(x,y) 决定,与邻域像素、空间坐标 ( x , y ) (x,y) (x,y) 无关,满足 s ( x , y ) = T ( r ( x , y ) ) s(x,y)=T\big(r(x,y)\big) s(x,y)=T(r(x,y)),空间位置仅用于遍历,不参与映射,图像几何结构保持不变。
- 无空间邻域运算:不同于卷积、滤波等邻域操作,点运算只依赖自身灰度值,不含邻域求和与加权,是逐像素独立计算。
- 值域合法性约束 :实际处理中必须满足 0 ≤ s ≤ L − 1 0\le s\le L-1 0≤s≤L−1,超出区间需截断或归一化,确保输出为有效灰度。
灰度变换的线性变换、非线性变换、直方图均衡化与直方图匹配,本质都是构造不同形式的映射函数 T ( r ) T(r) T(r),均属于点运算的具体实现。
二、灰度变换的常见类型
灰度变换根据映射函数 T ( r ) T(r) T(r) 的不同,分为三大经典类型,结合点运算原理,分别适用于不同的图像增强场景,具体如下:
1. 线性灰度变换
线性灰度变换的映射函数为线性关系: s = k r + b s = kr + b s=kr+b,其中 k k k(斜率)决定对比度 变化, b b b(截距)决定图像整体明暗偏移,是最直观的灰度调整方式。
- 当 k > 1 k>1 k>1:增强对比度,亮区更亮、暗区更暗,突出图像细节;
- 当 0 < k < 1 0<k<1 0<k<1:降低对比度,图像灰度分布趋于平缓;
- 当 k = − 1 , b = 255 k=-1,\;b=255 k=−1,b=255:实现灰度反转,亮暗区域互换,突出反色特征。
2. 非线性灰度变换
非线性灰度变换采用非线性映射函数,可针对性优化暗区或亮区细节,处理灰度分布不均的场景,常用两种形式:
- 对数变换: s = c ⋅ log ( 1 + r ) s = c\cdot\log(1 + r) s=c⋅log(1+r)( c c c 为调节常数),侧重增强暗区细节 、压缩高亮度范围,适合亮区过度饱和的图像;
- 伽马变换(幂次变换): s = c ⋅ r γ s = c\cdot r^\gamma s=c⋅rγ( c 、 γ c、\gamma c、γ 为常数),通过调整 γ \gamma γ 灵活控制明暗增强程度,在曝光校正、图像去雾等场景广泛使用。
3. 分段灰度变换
分段灰度变换将 [ 0 , L − 1 ] [0,L-1] [0,L−1] 整个灰度区间划分为多段,每段采用独立映射函数,可精准增强指定灰度区间的细节。常用形式:
- 阈值分段变换:仅对设定灰度范围内的像素做明暗调整,其余区间保持不变;
- 灰度窗口变换:只增强某一灰度窗口内的像素信息,常用于医学影像、工业检测中特定亮度目标的提取。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
img_path = "test.jpg"
img = cv2.imread(img_path, cv2.IMREAD_GRAYSCALE)
if img is None:
print(f"警告:无法读取图片 {img_path},自动生成模拟灰度图")
img = np.uint8(np.random.normal(100, 30, (400, 400)))
img = np.clip(img, 0, 255)
if np.max(img) == 0:
print("警告:图像全黑,自动添加微小亮度值避免计算错误")
img = np.clip(img + 1, 0, 255)
# 2. 线性灰度变换
# 对比度增强
k = 1.5
b = 20
linear_enhance = np.clip(k * img + b, 0, 255).astype(np.uint8)
# 灰度反转
linear_invert = 255 - img
# 3. 非线性灰度变换
# 先将图像转换为float64,提升运算精度,避免uint8溢出
img_float = img.astype(np.float64)
img_max = np.max(img_float)
# 对数变换
c_log = 255 / np.log(1 + img_max + 1e-8)
log_transform = c_log * np.log(1 + img_float)
log_transform = np.uint8(np.clip(log_transform, 0, 255))
# 伽马变换
gamma = 0.5
c_gamma = 255 / (img_max ** gamma + 1e-8)
gamma_transform = c_gamma * (img_float ** gamma)
gamma_transform = np.uint8(np.clip(gamma_transform, 0, 255))
# 4. 分段灰度变换
def piecewise_transform(pixel):
if 0 <= pixel < 100:
return np.uint8(pixel * 0.5)
elif 100 <= pixel < 200:
return np.uint8((pixel - 100) * 2 + 50)
else:
return np.uint8((pixel - 200) * 0.5 + 200)
piecewise_vec = np.vectorize(piecewise_transform)
piecewise_transform_img = piecewise_vec(img)
# 5. 结果可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.flatten()
titles = ["原始图像", "线性对比度增强", "灰度反转",
"对数变换", "伽马变换(gamma=0.5)", "分段灰度变换"]
imgs = [img, linear_enhance, linear_invert,
log_transform, gamma_transform, piecewise_transform_img]
for ax, img_show, title in zip(axes, imgs, titles):
ax.imshow(img_show, cmap="gray")
ax.set_title(title)
ax.axis("off")
plt.tight_layout()
plt.show()
三、直方图均衡化与直方图匹配
直方图均衡化与直方图匹配均是基于图像灰度直方图的点运算,属于灰度变换的延伸应用,核心目标是通过构造映射函数 s = T ( r ) s=T(r) s=T(r) 优化灰度分布、提升图像对比度,二者在数学目标与实现逻辑上存在明显差异:
1. 直方图均衡化
设8位灰度图像总像素数为 N N N,灰度级为 L = 256 L=256 L=256,第 k k k 级灰度出现的像素个数为 n k n_k nk,则该灰度级的概率密度 (归一化直方图)定义为:
p r ( r k ) = n k N , k = 0 , 1 , ... , L − 1 p_r(r_k)=\displaystyle\frac{n_k}{N},\quad k=0,1,\dots,L-1 pr(rk)=Nnk,k=0,1,...,L−1
,满足
∑ k = 0 L − 1 p r ( r k ) = 1 \sum_{k=0}^{L-1}p_r(r_k)=1 k=0∑L−1pr(rk)=1
-
核心数学原理
构造累积分布函数(CDF)作为点运算映射关系:
s k = T ( r k ) = ∑ i = 0 k p r ( r i ) = ( L − 1 ) ∑ i = 0 k n i N s_k=T(r_k)=\sum_{i=0}^{k}p_r(r_i)=(L-1)\sum_{i=0}^{k}\frac{n_i}{N} sk=T(rk)=i=0∑kpr(ri)=(L−1)i=0∑kNni该变换将原始集中分布的 p r ( r ) p_r(r) pr(r) 映射为近似均匀分布的 p s ( s ) p_s(s) ps(s),使灰度铺满 [ 0 , 255 ] [0,255] [0,255] 区间,从而全局提升对比度。
-
特点
映射函数由图像直方图唯一确定,全自动无参数,实现简单;但对噪声敏感,易在低纹理区域出现噪声过度增强,变换结果不可人为调节。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取灰度图像
img = cv2.imread("test.jpg", cv2.IMREAD_GRAYSCALE)
def manual_hist_equalize(img):
N = img.size
L = 256
hist, _ = np.histogram(img.flatten(), bins=L, range=(0, L))
cdf = hist.cumsum()
cdf_normalized = cdf / N
cdf_mapped = (L - 1) * cdf_normalized
cdf_mapped = np.uint8(np.clip(cdf_mapped, 0, 255))
img_equalized = cdf_mapped[img]
return img_equalized, hist, cdf_normalized
# 执行手动均衡化
img_manual_eq, hist_original, cdf_original = manual_hist_equalize(img)
# OpenCV内置均衡化
img_cv_eq = cv2.equalizeHist(img)
# 计算均衡化后直方图
hist_manual_eq, _ = np.histogram(img_manual_eq.flatten(), bins=256, range=(0, 256))
hist_cv_eq, _ = np.histogram(img_cv_eq.flatten(), bins=256, range=(0, 256))
# 结果可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
fig, axes = plt.subplots(3, 2, figsize=(12, 15))
axes = axes.flatten()
axes[0].imshow(img, cmap="gray")
axes[0].set_title("原始图像")
axes[0].axis("off")
axes[1].plot(hist_original, color="black")
axes[1].set_title("原始图像直方图")
axes[1].set_xlim([0, 255])
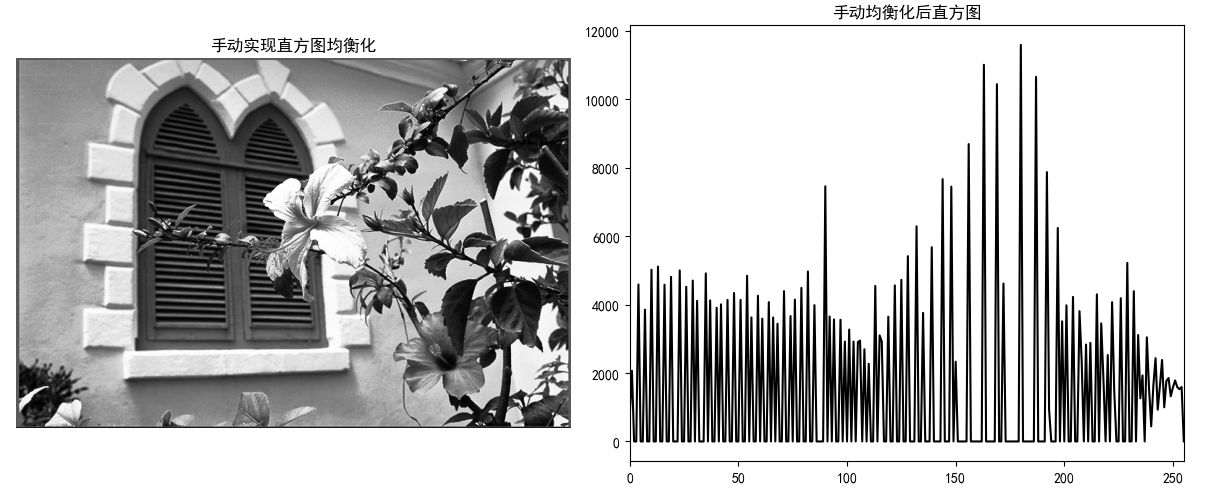
axes[2].imshow(img_manual_eq, cmap="gray")
axes[2].set_title("手动实现直方图均衡化")
axes[2].axis("off")
axes[3].plot(hist_manual_eq, color="black")
axes[3].set_title("手动均衡化后直方图")
axes[3].set_xlim([0, 255])
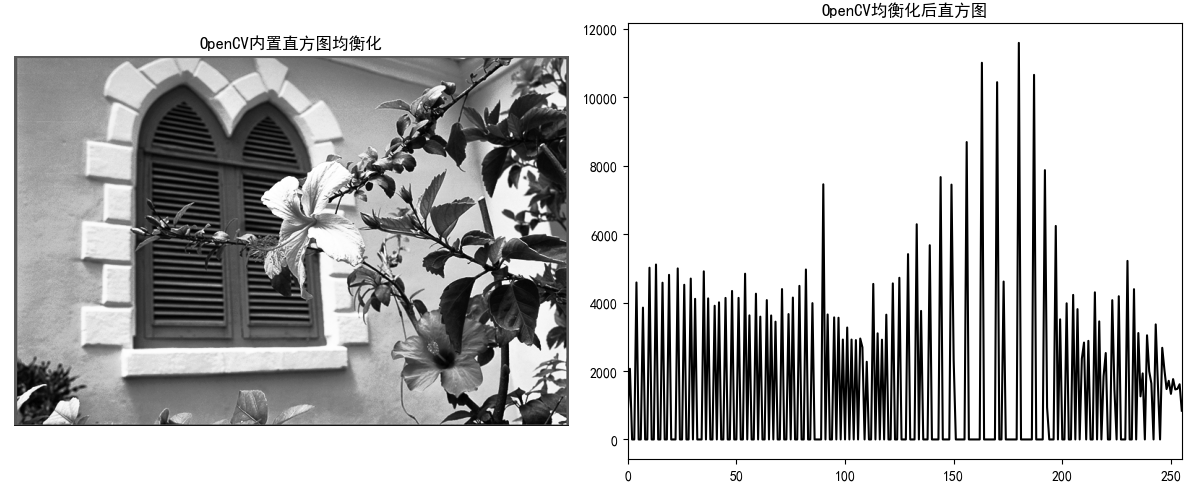
axes[4].imshow(img_cv_eq, cmap="gray")
axes[4].set_title("OpenCV内置直方图均衡化")
axes[4].axis("off")
axes[5].plot(hist_cv_eq, color="black")
axes[5].set_title("OpenCV均衡化后直方图")
axes[5].set_xlim([0, 255])
plt.tight_layout()
plt.show()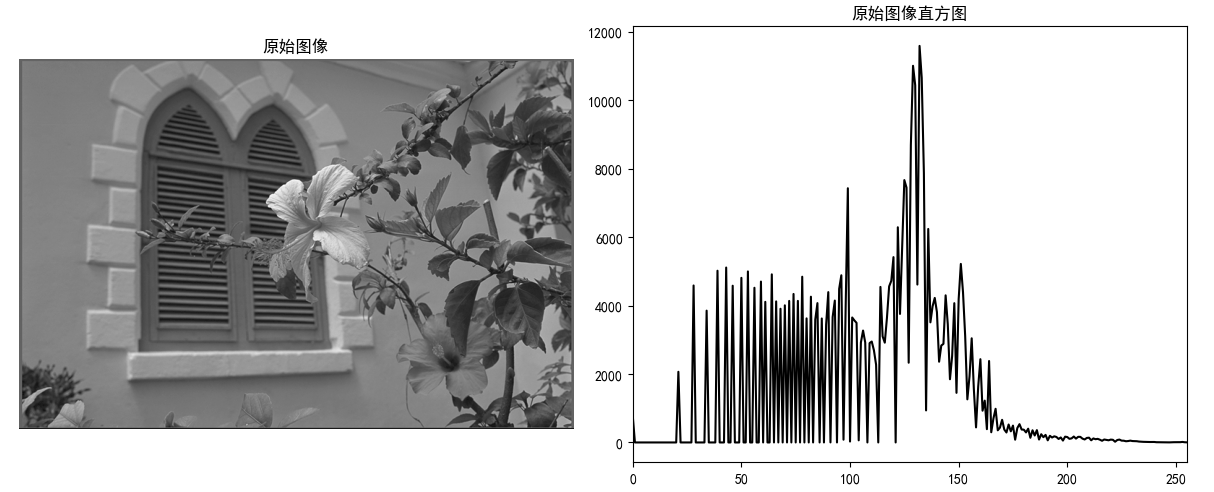
2. 直方图匹配(直方图规定化)
- 核心数学原理
给定原始图像分布 p r ( r ) p_r(r) pr(r),指定目标理想分布 p z ( z ) p_z(z) pz(z),分别计算二者累积分布:- 原始累积分布: s = T r ( r ) = ∫ 0 r p r ( τ ) d τ s=T_r(r)=\int_0^r p_r(\tau)d\tau s=Tr(r)=∫0rpr(τ)dτ
- 目标累积分布: s = T z ( z ) = ∫ 0 z p z ( τ ) d τ s=T_z(z)=\int_0^z p_z(\tau)d\tau s=Tz(z)=∫0zpz(τ)dτ
联立得到最终点运算映射: z = T z − 1 ( T r ( r ) ) z=T_z^{-1}(T_r(r)) z=Tz−1(Tr(r)),即先将原图映射为均匀分布 s s s,再由均匀分布映射为目标分布 z z z。
- 特点
可将图像灰度分布强制拟合为指定形态,增强过程可控,有效缓解均衡化过度放大噪声的问题,适用于图像拼接、多图亮度归一化、特定风格增强等场景。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取原始图像与参考图像
img_source = cv2.imread("test.jpg", cv2.IMREAD_GRAYSCALE)
img_reference = cv2.imread("reference.jpg", cv2.IMREAD_GRAYSCALE)
# 备用:生成模拟图像(无参考图时启用)
# img_source = np.uint8(np.random.normal(100, 30, (400, 400)))
# img_reference = np.uint8(np.random.normal(180, 40, (400, 400)))
# img_source, img_reference = np.clip(img_source, 0, 255), np.clip(img_reference, 0, 255)
def hist_match(source, reference):
def get_cdf(img):
N = img.size
hist, _ = np.histogram(img.flatten(), bins=256, range=(0, 256))
cdf = hist.cumsum()
cdf = cdf / N
cdf = np.clip(cdf, 0, 1)
return hist, cdf
hist_src, cdf_src = get_cdf(source)
hist_ref, cdf_ref = get_cdf(reference)
mapping_table = np.zeros(256, dtype=np.uint8)
for i in range(256):
min_diff = np.min(np.abs(cdf_ref - cdf_src[i]))
matching_idx = np.where(np.abs(cdf_ref - cdf_src[i]) == min_diff)[0][0]
mapping_table[i] = matching_idx
img_matched = mapping_table[source]
return img_matched, hist_src, hist_ref, hist_match_result(img_matched)
def hist_match_result(img):
hist, _ = np.histogram(img.flatten(), bins=256, range=(0, 256))
return hist
# 执行直方图匹配
img_matched, hist_src, hist_ref, hist_matched = hist_match(img_source, img_reference)
# 结果可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
fig, axes = plt.subplots(3, 2, figsize=(12, 15))
axes = axes.flatten()
axes[0].imshow(img_source, cmap="gray")
axes[0].set_title("原始图像(待匹配)")
axes[0].axis("off")
axes[1].plot(hist_src, color="black")
axes[1].set_title("原始图像直方图")
axes[1].set_xlim([0, 255])
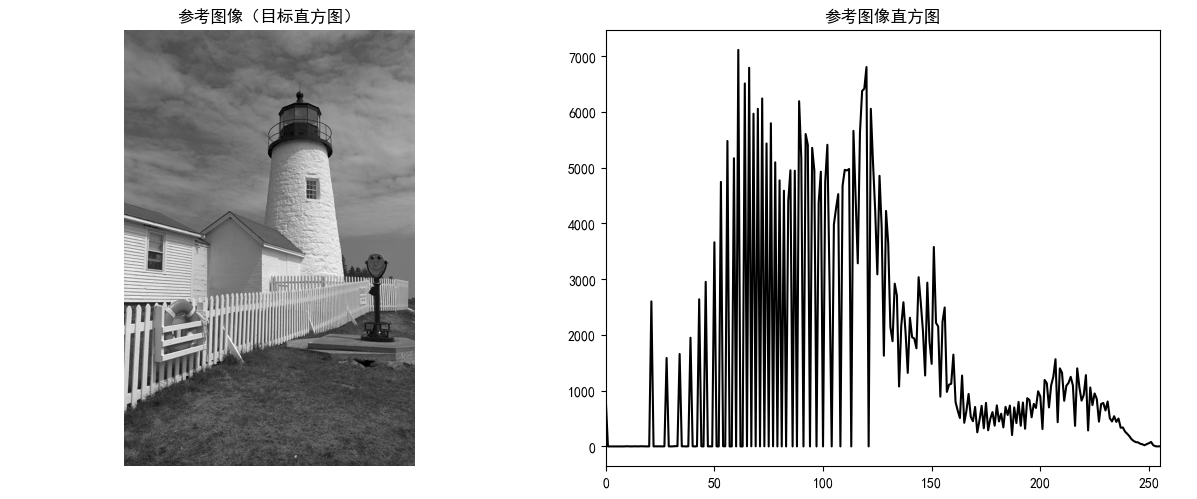
axes[2].imshow(img_reference, cmap="gray")
axes[2].set_title("参考图像(目标直方图)")
axes[2].axis("off")
axes[3].plot(hist_ref, color="black")
axes[3].set_title("参考图像直方图")
axes[3].set_xlim([0, 255])
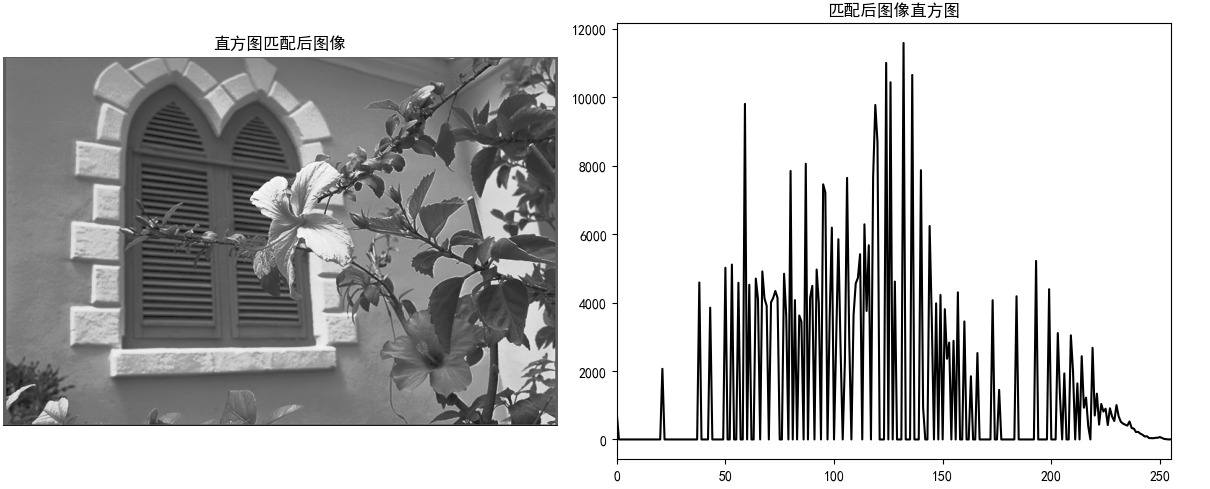
axes[4].imshow(img_matched, cmap="gray")
axes[4].set_title("直方图匹配后图像")
axes[4].axis("off")
axes[5].plot(hist_matched, color="black")
axes[5].set_title("匹配后图像直方图")
axes[5].set_xlim([0, 255])
plt.tight_layout()
plt.show()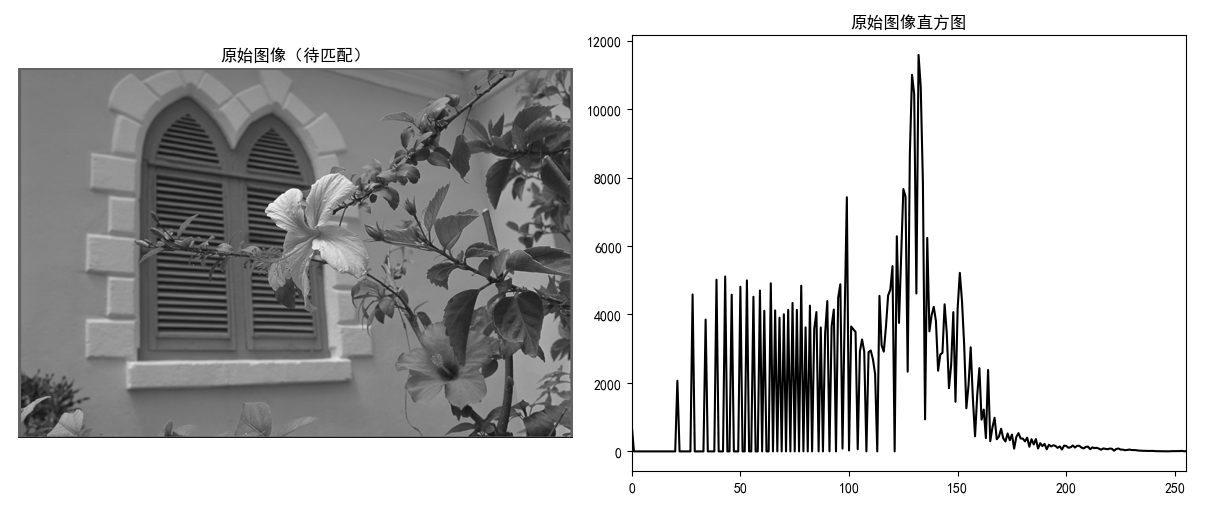
Ⅲ、图像阈值化与二值化
经过灰度变换优化后的图像,下一步核心操作是阈值化与二值化 。其中二值化是将灰度图像转换为仅包含黑( 0 0 0)、白( 255 255 255)两种灰度值的图像,而阈值化是实现二值化的核心手段------通过设定灰度阈值 T T T,将像素灰度值 r r r 与 T T T 比较,按规则映射为黑白像素,核心映射关系为:
s ( x , y ) = { 255 if r ( x , y ) ≥ T 0 if r ( x , y ) < T s(x,y) = \begin{cases} 255 & \text{if } r(x,y) \ge T \\ 0 & \text{if } r(x,y) < T \end{cases} s(x,y)={2550if r(x,y)≥Tif r(x,y)<T
(也可反向映射,即 r ( x , y ) ≥ T r(x,y) \ge T r(x,y)≥T 为 0 0 0, r ( x , y ) < T r(x,y) < T r(x,y)<T 为 255 255 255,根据前景/背景定义调整)。
根据阈值 T T T 的选取方式不同,阈值化可分为全局阈值化 (含Otsu自动阈值)和自适应阈值化,前者适用于光照均匀的图像,后者适用于光照不均、局部明暗差异大的场景,最终均实现图像二值化,凸显目标轮廓。
一、 全局阈值化
全局阈值化是最基础的二值化方法,其核心特点是整幅图像采用单一固定阈值 T T T,该阈值可人工手动设定,也可通过算法自动计算(如Otsu),映射规则统一应用于所有像素。
- 核心原理
选定一个全局阈值 T ∈ [ 0 , 255 ] T\in[0,255] T∈[0,255],对整幅图像执行前文的二值化映射,将像素划分为前景 (通常为目标,对应 255 255 255 或 0 0 0)和背景,实现目标与背景的初步分割。 - 手动全局阈值
阈值 T T T 由人工根据图像灰度分布经验设定,例如对于明暗对比明显的图像,可选取灰度直方图的波谷值作为 T T T。- 优点:实现简单、运算速度快、可精准控制分割效果;
- 缺点:对光照敏感、无法适配局部明暗差异,需反复调试阈值,通用性差。
- 适用场景
光照均匀、前景与背景灰度分布差异显著的图像(如扫描文档、光照均匀的工业零件图)。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取灰度图像
img = cv2.imread("test.jpg", cv2.IMREAD_GRAYSCALE)
# 容错处理:读取失败生成模拟图像
if img is None:
print("警告:读取图片失败,自动生成模拟灰度图")
img = np.uint8(np.random.normal(127, 50, (400, 400)))
img = np.clip(img, 0, 255)
# 1. 手动全局阈值化(阈值T=127,可自行调整)
T_manual = 127
_, img_global_manual = cv2.threshold(img, T_manual, 255, cv2.THRESH_BINARY)
# 2. 自动全局阈值化(以图像平均灰度作为阈值)
T_auto = np.mean(img).astype(np.uint8)
_, img_global_auto = cv2.threshold(img, T_auto, 255, cv2.THRESH_BINARY)
# 结果可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# 绘制图像
axes[0].imshow(img, cmap="gray")
axes[0].set_title("原始灰度图像")
axes[0].axis("off")
axes[1].imshow(img_global_manual, cmap="gray")
axes[1].set_title(f"手动全局阈值(T={T_manual})")
axes[1].axis("off")
axes[2].imshow(img_global_auto, cmap="gray")
axes[2].set_title(f"自动全局阈值(T={T_auto})")
axes[2].axis("off")
plt.tight_layout()
plt.show()
二、 Otsu阈值化(最大类间方差法)
Otsu阈值化是全局自动阈值化 的经典算法,无需人工设定阈值 T T T,通过数学方法自动寻找最优全局阈值,解决了手动全局阈值的通用性问题。
1. 核心数学原理
假设将图像像素按阈值 T T T 划分为两类 C 0 C_0 C0(灰度 < T < T <T,背景)和 C 1 C_1 C1(灰度 ≥ T \ge T ≥T,前景),计算两类的类间方差 ,最优阈值 T o p t T_{opt} Topt 是使类间方差最大的灰度值。
-
设图像总像素数为 N N N, C 0 C_0 C0 像素数为 N 0 N_0 N0, C 1 C_1 C1 像素数为 N 1 N_1 N1,则两类像素占比:
P 0 = N 0 N , P 1 = N 1 N P_0 = \frac{N_0}{N},\quad P_1 = \frac{N_1}{N} P0=NN0,P1=NN1满足 P 0 + P 1 = 1 P_0 + P_1 = 1 P0+P1=1。
-
设 C 0 C_0 C0 平均灰度为 μ 0 \mu_0 μ0, C 1 C_1 C1 平均灰度为 μ 1 \mu_1 μ1,全局平均灰度:
μ = P 0 μ 0 + P 1 μ 1 \mu = P_0\mu_0 + P_1\mu_1 μ=P0μ0+P1μ1 -
类间方差定义:
σ 2 = P 0 ( μ 0 − μ ) 2 + P 1 ( μ 1 − μ ) 2 \sigma^2 = P_0(\mu_0 - \mu)^2 + P_1(\mu_1 - \mu)^2 σ2=P0(μ0−μ)2+P1(μ1−μ)2 -
遍历 T ∈ [ 0 , 255 ] T\in[0,255] T∈[0,255],使 σ 2 \sigma^2 σ2 最大的 T T T 即为最优Otsu阈值 T o p t T_{opt} Topt。
2. 算法特点
- 全自动无参数,无需人工调试,实现简单;
- 仅适用于全局光照相对均匀、直方图呈现双峰分布的图像(双峰对应前景与背景的灰度集中区);
- 对噪声敏感,噪声会模糊双峰分布,导致阈值选取偏差。
3. 适用场景
光照基本均匀、前景与背景灰度分离明显(直方图双峰)的图像,是工程上最常用的全局自动二值化方法。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取灰度图像
img = cv2.imread("test.jpg", cv2.IMREAD_GRAYSCALE)
# 容错处理:读取失败生成模拟图像(双峰分布,适配Otsu)
if img is None:
print("警告:读取图片失败,自动生成双峰分布模拟图")
img1 = np.uint8(np.random.normal(80, 20, (400, 200)))
img2 = np.uint8(np.random.normal(200, 20, (400, 200)))
img = np.hstack((img1, img2))
img = np.clip(img, 0, 255)
# Otsu阈值化(自动寻找最优阈值)
# 返回值:ret=最优Otsu阈值,img_otsu=二值化图像
ret_otsu, img_otsu = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
# 计算原始图像直方图(用于验证双峰分布)
hist, _ = np.histogram(img.flatten(), bins=256, range=(0, 256))
# 结果可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# 绘制图像
axes[0].imshow(img, cmap="gray")
axes[0].set_title("原始灰度图像")
axes[0].axis("off")
axes[1].plot(hist, color="black")
axes[1].set_title("原始图像直方图(双峰分布)")
axes[1].set_xlim([0, 255])
axes[1].axvline(x=ret_otsu, color="red", linestyle="--", label=f"Otsu阈值={ret_otsu}")
axes[1].legend()
axes[2].imshow(img_otsu, cmap="gray")
axes[2].set_title(f"Otsu二值化(最优阈值T={ret_otsu})")
axes[2].axis("off")
plt.tight_layout()
plt.show()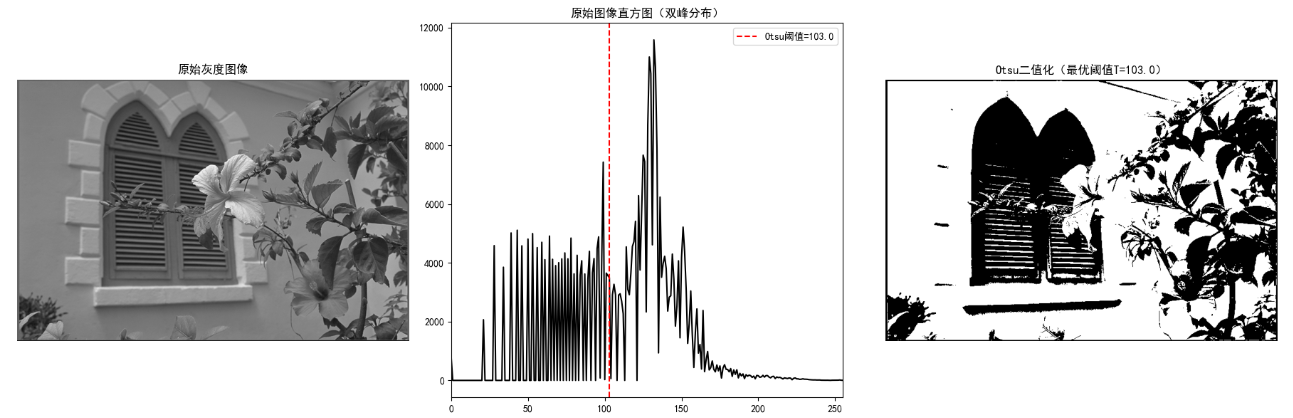
三、 自适应阈值化
自适应阈值化(又称局部阈值化)针对光照不均、局部明暗差异大的图像,其核心特点是不为整幅图像设定单一阈值,而是为每个像素点动态计算其局部邻域内的阈值 T ( x , y ) T(x,y) T(x,y),再以该局部阈值对当前像素进行二值化。
1. 核心原理
- 为每个像素 ( x , y ) (x,y) (x,y) 确定一个局部邻域(通常为正方形窗口,如 15 × 15 15\times15 15×15);
- 计算该邻域内像素的平均灰度或高斯加权平均灰度,作为当前像素的局部阈值 T ( x , y ) T(x,y) T(x,y);
- 用 T ( x , y ) T(x,y) T(x,y) 对像素 ( x , y ) (x,y) (x,y) 执行二值化映射,完成局部分割。
2. 常见类型
- 均值自适应阈值:以局部邻域的平均灰度作为阈值,实现简单,易受噪声影响;
- 高斯自适应阈值:以局部邻域的高斯加权平均灰度作为阈值,对噪声有一定抑制作用,效果更稳定。
3. 算法特点
- 可有效处理光照不均、局部明暗差异大的图像,分割效果优于全局阈值化;
- 需设定邻域窗口大小等参数,运算量大于全局阈值化;
- 对局部噪声有一定容忍度,不易出现大面积误分割。
4. 适用场景
光照不均的图像(如逆光拍摄的文档、表面有明暗渐变的物体、复杂场景下的目标提取)。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取灰度图像
img = cv2.imread("test2.jpg", cv2.IMREAD_GRAYSCALE)
# 容错处理:读取失败生成光照不均模拟图(适配自适应阈值)
if img is None:
print("警告:读取图片失败,自动生成光照不均模拟图")
img = np.uint8(np.zeros((400, 600)))
img[:, :200] = np.random.normal(80, 10, (400, 200))
img[:, 200:400] = np.random.normal(150, 10, (400, 200))
img[:, 400:] = np.random.normal(220, 10, (400, 200))
img = np.clip(img, 0, 255)
# 1. 均值自适应阈值化
# blockSize=邻域窗口大小(必须为奇数),C=常数(从平均值中减去的数值)
img_adaptive_mean = cv2.adaptiveThreshold(
img, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, blockSize=15, C=2
)
# 2. 高斯自适应阈值化
img_adaptive_gauss = cv2.adaptiveThreshold(
img, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, blockSize=15, C=2
)
# 结果可视化
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# 绘制图像
axes[0].imshow(img, cmap="gray")
axes[0].set_title("原始灰度图像(光照不均)")
axes[0].axis("off")
axes[1].imshow(img_adaptive_mean, cmap="gray")
axes[1].set_title("均值自适应阈值二值化")
axes[1].axis("off")
axes[2].imshow(img_adaptive_gauss, cmap="gray")
axes[2].set_title("高斯自适应阈值二值化")
axes[2].axis("off")
plt.tight_layout()
plt.show()
四、 二值化结果与应用
无论是全局阈值、Otsu还是自适应阈值,最终目标都是实现高质量的图像二值化,二值化后的图像具有灰度值简单、数据量小、目标轮廓清晰的特点,在计算机视觉中具有广泛应用:
- 文档处理:扫描文档的文字提取、表格分割、印章识别;
- 工业检测:零件缺陷检测、尺寸测量、条形码/二维码识别;
- 目标提取:前景目标轮廓提取、特征点检测(如角点、边缘)的前置步骤;
- 图像压缩:二值图像数据量仅为8位灰度图的1/8,便于存储和传输。
优质的二值化结果依赖于前期灰度变换的优化和阈值方法的合理选择,需根据图像的光照条件、灰度分布特点灵活选用对应的阈值化策略。
Ⅳ、总结
本文围绕图像灰度变换 与阈值化二值化两大核心预处理技术,将核心知识点、选型准则与实践要点整理如下表:
| 技术方向 | 核心本质 | 关键方法 | 适用场景 | 实践注意事项 |
|---|---|---|---|---|
| 灰度变换 | 通过点运算映射函数 s = T ( r ) s=T(r) s=T(r) 优化图像对比度与明暗分布 | 线性变换(对比度增强、反转) 非线性变换(对数、伽马) 分段灰度变换 直方图均衡化/匹配 | 1. 图像对比度低、灰度分布集中 2. 需要统一多图灰度风格 | 直方图均衡化易放大噪声,可配合滤波使用 |
| 阈值化二值化 | 设定阈值 T T T,将灰度图转换为黑白二值图,实现前景与背景分离 | 全局阈值化(手动/自动) Otsu阈值化 自适应阈值化(均值/高斯) | 1. 光照均匀、前景背景差异显著 → 全局/Otsu阈值化 2. 光照不均、局部明暗差异大 → 自适应阈值化(高斯型更优) | 1. 自适应阈值的blockSize需为奇数 2. 可调整参数实现反向二值化 3. 预处理增加滤波可提升效果 |
核心结论
图像灰度变换与阈值化二值化是计算机视觉领域的基础核心预处理技术,具有实现简单、运算高效、部署成本低的特点,在文档处理、工业检测、简单场景目标提取等领域仍具有不可替代的价值。掌握不同方法的适用场景与选型准则,是实现高质量图像预处理的关键。