目录
---
1.摘要
本文提出了一种新型异质综合学习粒子群算法(HCLPSO),其结合低差异序列(LDS)和共轭梯度法(CG)以提升优化性能。本文提出了两种HCLPSO变种:HCLPSO-DC和HCLPSO-OC,分别通过动态进化序列和优化Halton序列生成LDS。每个变种都采用两种新颖的速度更新策略(VUS):基于LDS的VUS(LDS-VUS)和基于复合共轭梯度的VUS(CCG-VUS),并结合自适应切换策略,以决定使用哪种VUS来进行种群搜索。LDS-VUS通过增强搜索空间覆盖能力提高整体搜索能力,而CCG-VUS则引导粒子沿共轭方向进行搜索,从而提升开发能力。
2.提出的算法
基于 LDS 的速度更新策略
LDS-VUS通过利用LDS的强空间覆盖能力,显著改善了HCLPSO的探索和开发能力。通过Hadamard积引入LDS的优势,增加了探索子种群和开发子种群的多样性,速度更新:
v g + 1 , i = { w g v g , i + k g P i ( 1 ) ∘ ( p g , i − x g , i ) , 1 ≤ i ≤ N 1 w g v g , i + c g , 1 P i ( 2 ) ∘ ( p g , i − x g , i ) + c g , 2 ϵ g , 3 , i ∘ ( x g , b e s t − x g , i ) , N 1 < i ≤ N v_{g+1,i} = \begin{cases} w_g v_{g,i} + k_g P^{(1)}i \circ (p{g,i} - x_{g,i}), & 1 \leq i \leq N_1 \\ w_g v_{g,i} + c_{g,1} P^{(2)}i \circ (p{g,i} - x_{g,i}) + c_{g,2} \epsilon_{g,3,i} \circ (x_{g,best} - x_{g,i}), & N_1 < i \leq N \end{cases} vg+1,i={wgvg,i+kgPi(1)∘(pg,i−xg,i),wgvg,i+cg,1Pi(2)∘(pg,i−xg,i)+cg,2ϵg,3,i∘(xg,best−xg,i),1≤i≤N1N1<i≤N
在算法中引入自适应的切换策略,LDS-VUS能够有效地平衡探索和开发,提升HCLPSO在全局和局部搜索中的性能。
基于复合共轭梯度法的速度更新策略
本文提出了一种基于共轭梯度法(CGM)的复合速度更新策略(CCG-VUS),CCG-VUS通过引入CGM的精确共轭搜索方向 d g d_g dg来指导开发子种群的粒子搜索,从而提高局部搜索能力。速度更新公式:
v g + 1 , i = { w g v g , i + k g P i ( 1 ) ∘ ( p g , i − x g , i ) , 1 ≤ i ≤ N 1 w C G , g , i v g , i + c g , 1 P i ( 2 ) ∘ ( p g , i − x g , i ) + c g , 2 ϵ g , 3 , i ∘ ( x g , b e s t − x g , i ) , N 1 < i ≤ N v_{g+1,i} = \begin{cases} w_g v_{g,i} + k_g P^{(1)}i \circ (p{g,i} - x_{g,i}), & 1 \leq i \leq N_1 \\ w_{CG,g,i} v_{g,i} + c_{g,1} P^{(2)}i \circ (p{g,i} - x_{g,i}) + c_{g,2} \epsilon_{g,3,i} \circ (x_{g,best} - x_{g,i}), & N_1 < i \leq N \end{cases} vg+1,i={wgvg,i+kgPi(1)∘(pg,i−xg,i),wCG,g,ivg,i+cg,1Pi(2)∘(pg,i−xg,i)+cg,2ϵg,3,i∘(xg,best−xg,i),1≤i≤N1N1<i≤N
其中, w C G , g , i w_{CG,g,i} wCG,g,i 为基于CGM的共轭惯性系数,计算公式为:
w C G , g , i = β g , i = ∇ f g , i T ∇ f g , i ∇ f g − 1 , i T ∇ f g − 1 , i w_{CG,g,i}=\beta_{g,i}=\frac{\nabla f_{g,i}^T\nabla f_{g,i}}{\nabla f_{g-1,i}^T\nabla f_{g-1,i}} wCG,g,i=βg,i=∇fg−1,iT∇fg−1,i∇fg,iT∇fg,i
计算梯度 ∇ f g , i \nabla f_{g,i} ∇fg,i 使用LDS-VUS提供的信息:
∇ f g , i = − c g , 1 α g , i P i ( 2 ) ∘ ( p g , i − x g , i ) − c g , 2 α g , i ϵ g , 3 , i ∘ ( x g , b e s t − x g , i ) \nabla f_{g,i}=-\frac{c_{g,1}}{\alpha_{g,i}}P_i^{(2)}\circ(p_{g,i}-x_{g,i})-\frac{c_{g,2}}{\alpha_{g,i}}\epsilon_{g,3,i}\circ(x_{g,best}-x_{g,i}) ∇fg,i=−αg,icg,1Pi(2)∘(pg,i−xg,i)−αg,icg,2ϵg,3,i∘(xg,best−xg,i)
自适应切换策略
策略根据全局最优解的更新情况进行切换:当全局最优解正常更新时使用LDS-VUS,而当全局最优解在gCG次迭代后仍未更新时,使用CCG-VUS,引导粒子沿共轭搜索方向移动。
自适应切换策略中的gCG与问题维度D的关系为:
g_{CG} = \\text{floor}\\left( 4.769 \\times 10\^{-6} \\times D\^4 - 0.001053 \\times D\^3 + 0.06815 \\times D\^2 + 0.4494 \\times D + 0.2532 \\right)
3.结果展示
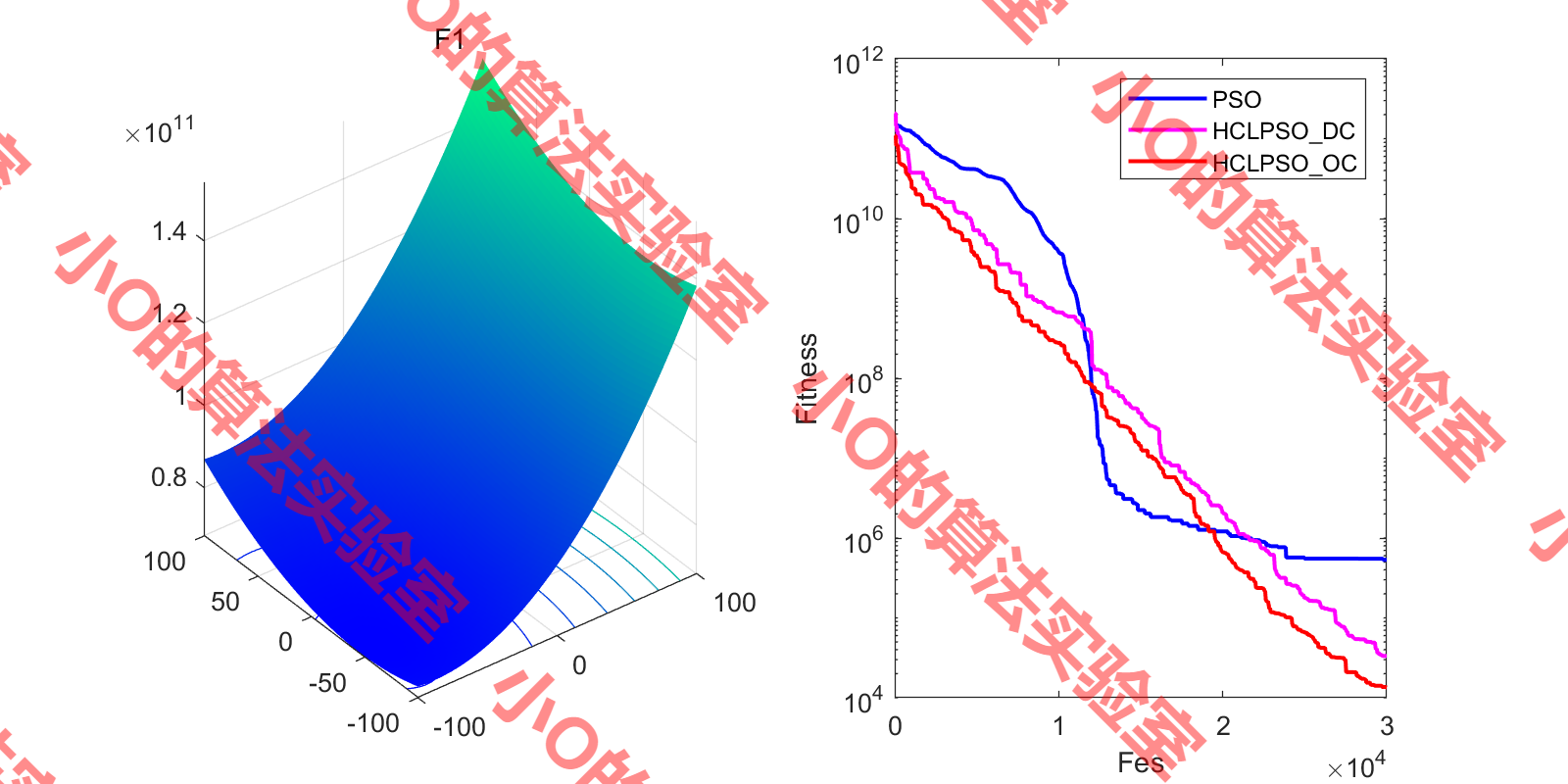
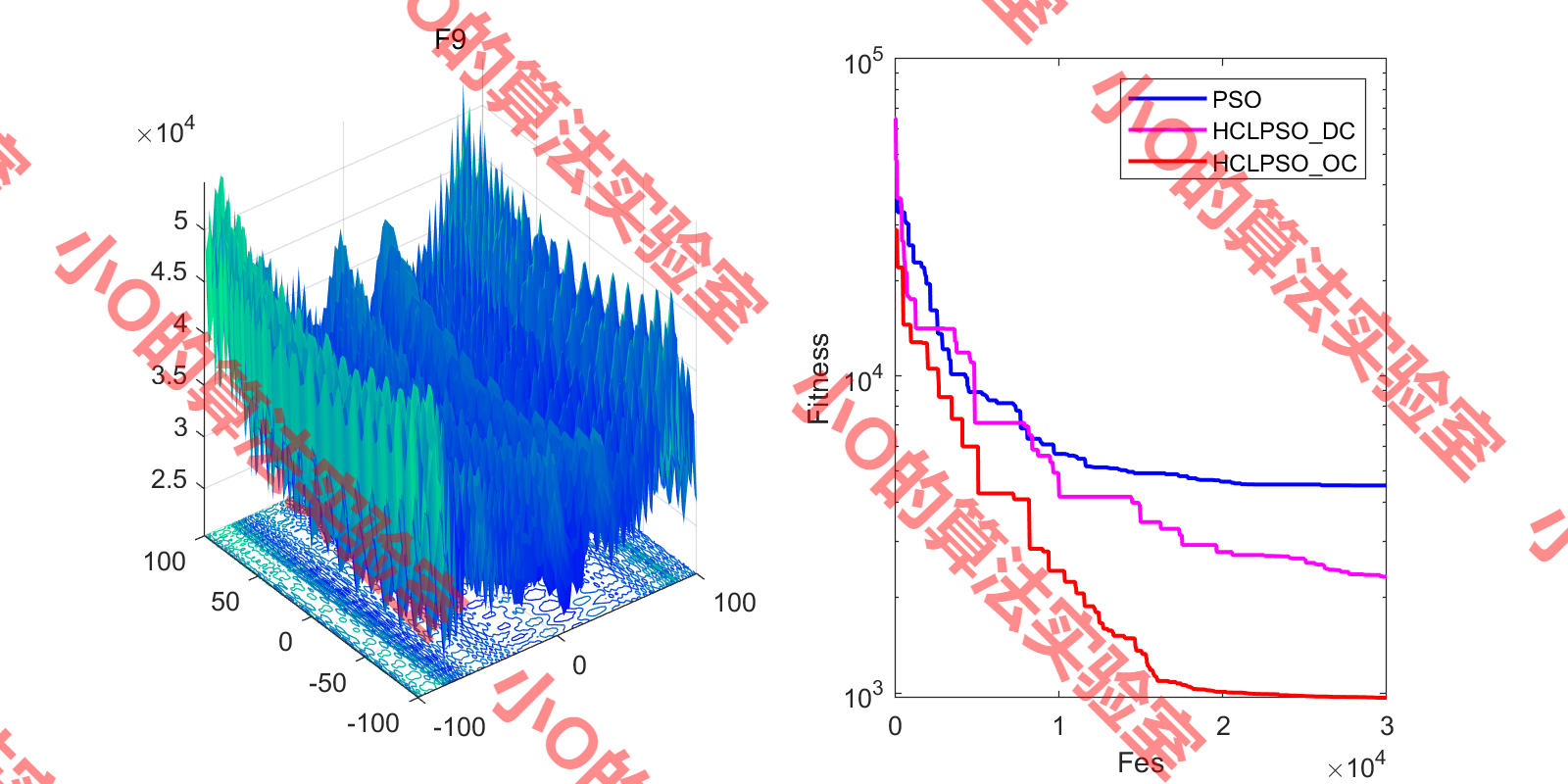
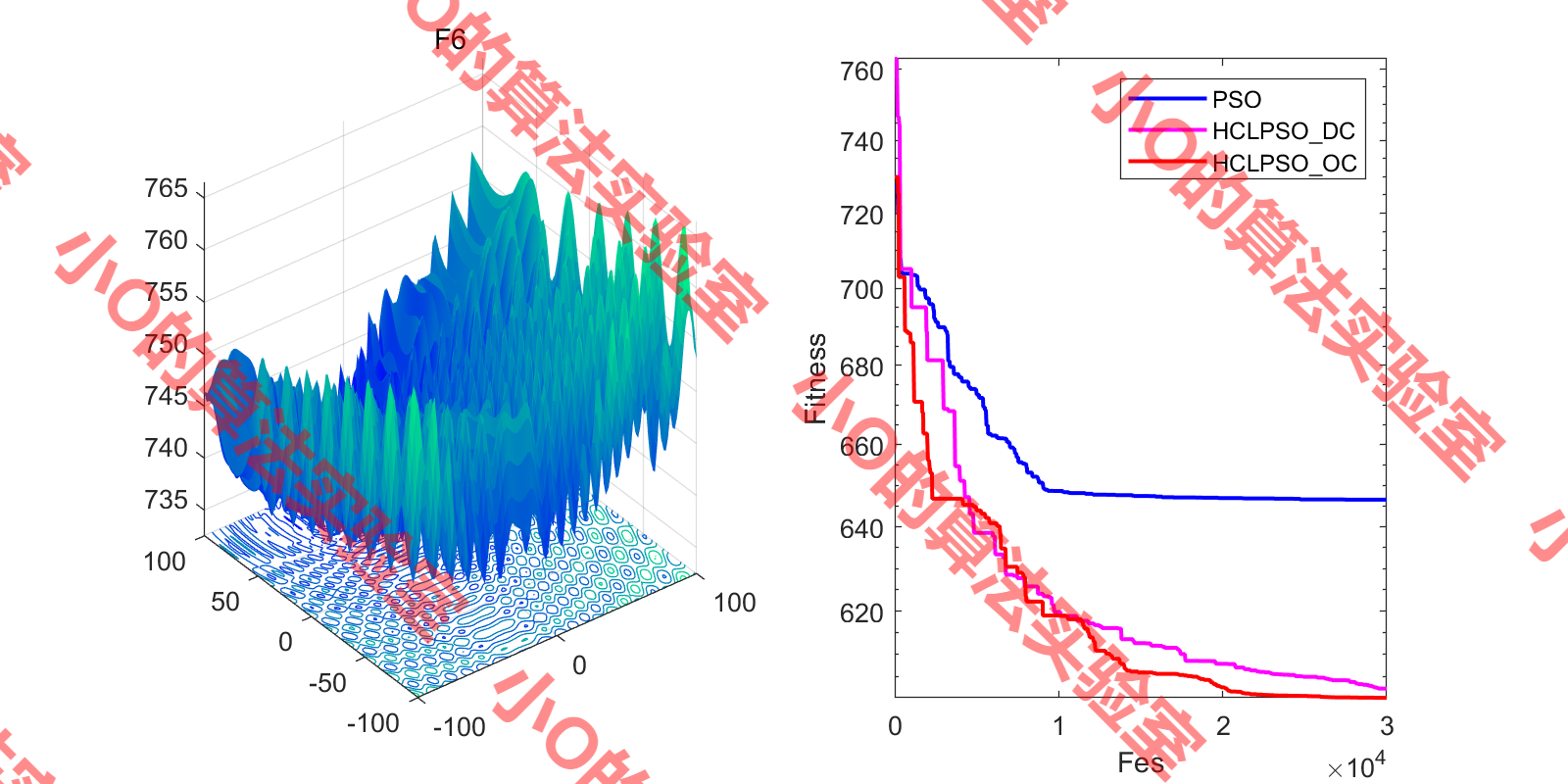
4.参考文献
1\] Zhao Y, Wu F, Pang J, et al. New heterogeneous comprehensive learning particle swarm optimizer enhanced with low-discrepancy sequences and conjugate gradient method\[J\]. Swarm and Evolutionary Computation, 2025, 93: 101848. ### 5.代码获取 xx ### 6.算法辅导·应用定制·读者交流 xx