昨天我们了解到了二叉树的基本概念,今天我们有必要了解一下二叉树的这种形式是如何在我们的C语言程序中体现的吧
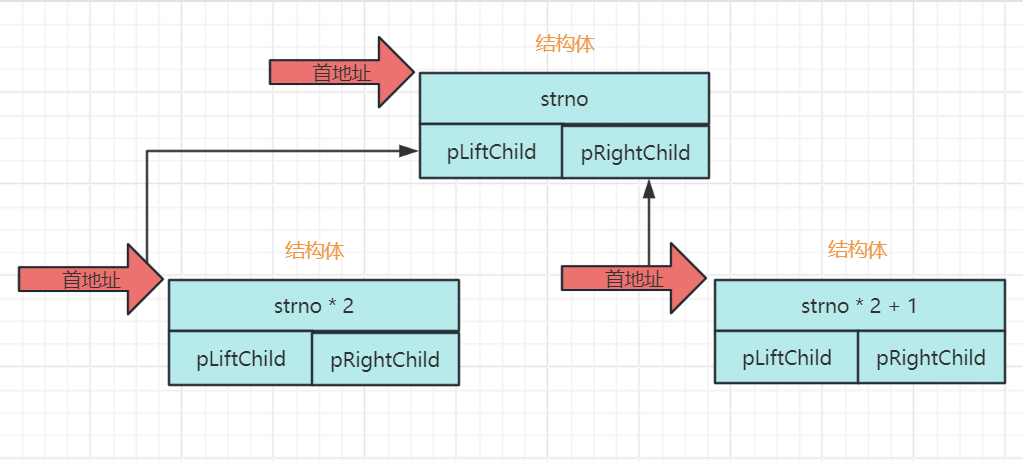
1.完全二叉树结构体定义:
c
typedef struct treenode
{
int no;
struct treenode *pliftchild;
struct treenode *prightchild;
}treenode_t;- no是节点编号
- pliftchild是左子树根节点首地址
- prightchild是右子树根节点首地址
接下来了解一下如何构建我们的完全二叉树
c
treenode_t *creatCompeteBtree(int stano,int endno)
{
if(stano > endno)
return NULL;
treenode_t pnewnode = NULL;
pnewnode = malloc(sizeof(treenode_t))
if(NULL = pnewnode)
{
perror("fail to malloc\n");
return NULL;
}
pnewnode->no = stano;
pnewnode->pliftchild = creatcompetebtree(stano * 2,endno);
pnewnode->prightchild = creatcompetebtree(stano * 2 +1 ,endno);
return pnewnode;
}
- 构建完全二叉树利用前序遍历的思想
- 先构建根节点,再构建左右子树;
- 会先构建出最左边的子树,再去构建右边的子树
3.深度遍历:
这里会体现出递归函数的极致调用
1.前序遍历:
c
int preOrderbtree(treenode_t *ptemrooot)
{
printf("%d ",ptemroot->no);
if(ptemroot->pliftchild != NULL)
preorderbtree(ptemroot->pliftchild);
if(ptrmroot->prightchild != NULL)
preordertree(ptemroot->prightchild);
return 0;
}2.中序遍历:
c
int inorder(treenode_t *ptemroot)
{
if(ptemroot->pliftchild != NULL)
inorder(ptemroot->pliftchild);
printf("%d ",ptemroot->no);
if(ptemroot->prightchild != NULL)
inorder(ptemroot->prightchild);
return 0;
}3.后序遍历:
c
int postorder(treenode_t *proot)
{
if(proot->pliftchild != NULL)
postorder(proot->pliftchild);
if(proot->pliftchild != NULL)
postorder(proot->prightchild);
printf("%d ",proot->no);
return 0;
}- 这里我们可以看到,这三种形式的深度遍历都是递归函数的调用
- 打印的位置取决于我们的遍历方式
4.层序遍历:
如何让我们一层一层的遍历二叉树元素呢?接下来我们就来了解一下
c
int layout(treenode_t *proot)
{
node_t *pqueue = NULL;
datatype ptem = NULL;
if(proot == NULL)
return 0;
pqueue = creatempty();
enterqueue(pqueue,proot)
while(!isempty(pquque))
{
ptem = quitqueue(pqueue);
printf("%d ",ptem->no);
if(ptem->pliftchile != NULL)
enterqueue(pqueue,ptem->pliftchild);
if(ptem->prightchild != NULL)
enterqueue(pqueue,ptem->prightchild);
}
return 0;
}
i
- 层序遍历中需要借助队列先入先出,后入后出的特性
- 先将根节点存进队列
- 在循环内部弹出根节点并打印,再让根节点的左右子树入队
- 当队列不为空时一直弹出节点并打印
5.二叉树的高度获取:
这里我们简单了解一下如何获取一个二叉树的高度:
c
int gethigh(treenode_t *proot)
{
int hlift = 0;
int hright = 0;
hlift = gethgh(proot->pliftchild);
hright = gethigh(proot->prightchild);
return (hlift > hright ? hlift : hright) + 1;
}这就是一个简单函数的递归调用
6.非完全二叉树的构建:
我们不用在指定顺序,可以按照前序遍历直接输入自己想构建的二叉树的顺序去进行构建
c
treenode_t *creat(int no)
{
treenode_t *pnew = NULL;
char ch = 0;
scanf(" %c",&ch);
if('#' == ch)
{
return NULL;
}
else
{
pnew = mallpc(sizeof(treenode_t));
if(pnew == NULL)
{
perror("fail to malloc\n");
return NULL;
}
pnew->ch = ch;
pnew->no = no;
pnew->pliftchild = creat(no *2);
pnew->prightchild = creat(no*2+1);
}
return pnew;
}以上的函数形式达成的效果都是要借助我们的递归函数来达成的,那如何不去使用递归函数来达到这三种形式的深度遍历呢??
我们可以借助栈的回溯能力来帮助我们达成这个效果
来看看吧:
利用非递归函数来实现对二叉树的遍历
1.前序遍历(入栈时打印)
c
int preorder(treenode_t *proot)
{
treenode *ptem = NULL;
node_t *pstack = NULL;
pstack = creatseqstack(50);
ptem = proot;
while(1)
{
while(ptem != NULL)
{
pushstack(pstack,ptem);
printf("%d ",ptem->no);
ptem = ptem ->pliftchild;
}
if(isemptystack(pstack))
break;
ptem = popstack(pstack);
ptem = ptem->prightchild;
}
destory(&pstack);
return 0;
}2.中序遍历:
c
int inorder(treenode_t *proot)
{
treenode *ptem = NULL;
node_t *pstack = NULL;
pstack = creatstack(60);
ptem = proot;
while(1)
{
while(ptem != NULL)
{
pushstack(pstack,ptem);
ptem = ptem->pliftchild;
}
if(isemptystack(pstack))
break;
ptem = popstack(pstack);
printf("%d ",ptem->no);
ptem = ptem->prightchild;
}
destory(&pstack);
return 0;
}3.后序遍历:
c
int postorder(treenode_t *proot)
{
treenode_t *ptem = NULL;
node_t *pstack = NULL;
pstack = creatstack(60);
while(1)
{
while(ptem != NULL)
{
pushstack(pstack,ptem);
ptem->flag = 1;
ptem = ptem->pliftchild;
}
if(isemptystack(pstack))
break;
ptem = popstack(pstack);
if(ptem->flag == 1)
{
ptem->flag = 0;
pushstack(pstack,ptem);
ptem = ptem->prightchild;
}
else if(ptem->flag == 0)
{
printf("%d ",ptem->no);
ptem = NULL;
}
}
destory(&pstack);
return 0
}接下来我们延伸一下哈希表的内容:
1.哈希思想:
将数据根据哈希算法映射成键值,根据键值来写入或查找数据,以实现查找数据哦(1)时间复杂度
2.哈希冲突:
多个数据通过哈希算法映射成同样的键值,这就说明产生了哈希冲突
3.链地址法(通过降低数据集来降低时间复杂度)
数据产生哈希冲突通过在同一键值用链表来实现多个数据的存储;
好的算法应该尽可能的降低哈希冲突